二叉樹遍歷分為三種：前序、中序、后序，其中序遍歷最為重要。為啥叫這個名字？是根據根節點的順序命名的。

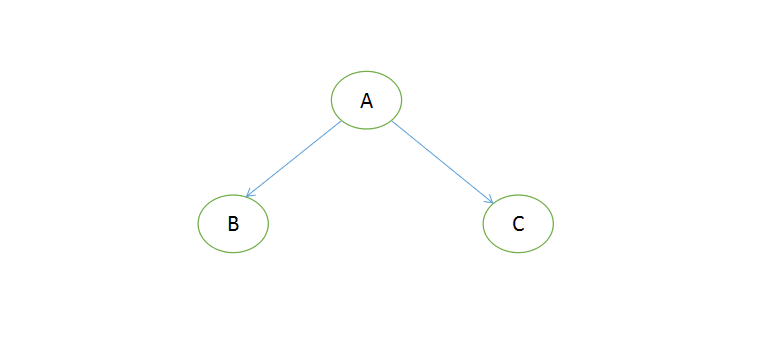
比如上圖正常的一個滿節點，A：根節點、B：左節點、C：右節點，前序順序是ABC(根節點排最先，然后同級先左后右)；中序順序是BAC(先左后根最后右)；后序順序是BCA(先左后右最后根)。

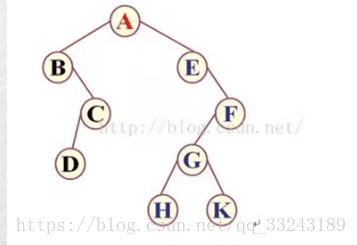
比如上圖二叉樹遍歷結果

前序遍歷：ABCDEFGHK

中序遍歷：BDCAEHGKF

后序遍歷：DCBHKGFEA

分析中序遍歷如下圖，中序比較重要(java很多樹排序是基于中序，后面講解分析)

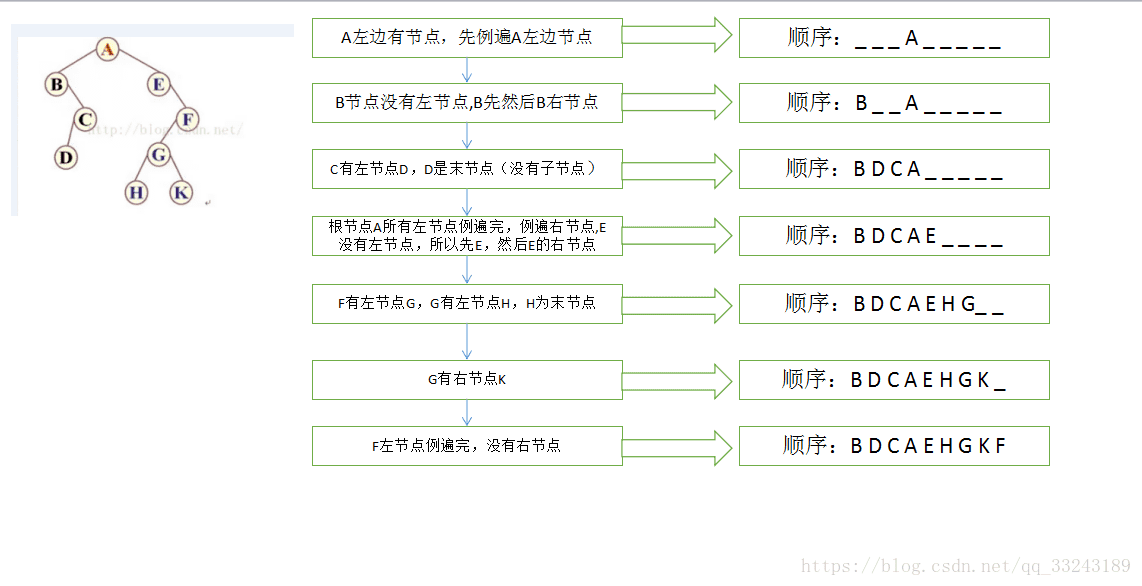
下面介紹一下，二叉樹的三種遍歷方式，其中每一種遍歷方式都有三種實現方式。

節點定義：

struct TreeNode

{

int val;

TreeNode *left,*right;

TreeNode(int val){

this->val = val;

this ->left = this->right = NULL;

}

};

先序遍歷

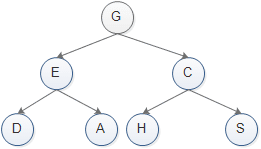
以上面這張圖為例：我們講講樹的三種遍歷方式：

先序遍歷：先訪問根節點，然后訪問左孩子，最后訪問右孩子。

所以，上面遍歷的結果是：GEDACHS。

下面，我們來看看具體代碼實現

1.遞歸實現

void preOrder(TreeNode *root){

if (root==NULL)

return;

cout<val<

preOrder(root->left);

preOrder(root->right);

}

2.使用輔助棧

實現思路：1.將根節點入棧

2.每次從棧頂彈出一個節點，訪問該節點

3.把當前節點的右孩子入棧

4.把當前節點的左孩子入棧

具體實現：

void preOrder2(TreeNode *root){

if (root == NULL)

return;

stack stk; //開辟一個棧空間

stk.push(root);

while(!stk.empty()){

TreeNode* pNode = stk.pop();

cout<val;

if (pNode->right!=NULL)

stk.push(pNode->right);

if (pNode->left!=NULL)

stk.push(pNode->left);

}

}

3.Morris遍歷

Morris遍歷，常數的空間即可在O(n)時間內完成二叉樹的遍歷。

O(1)空間進行遍歷困難之處在于在遍歷的子結點的時候如何重新返回其父節點？

在Morris遍歷算法中，通過修改葉子結點的左右空指針來指向其前驅或者后繼結點來實現的。

其本質：線索二叉樹(Threaded Binary Tree)，通過利用葉子節點空的right指針，指向中序遍歷的后繼節點，從而避免了對 stack 的依賴。

具體實現：

void preOrder(TreeNode* root){

if (root == NULL)

return;

TreeNode* pNode = root;

while(pNode != NULL){

if (pNode->left == NULL)

{

cout<val<

pNode = pNode->right;

}

else{

TreeNode* pPre = pNode->left;

while(pPre->right != NULL && pPre->right != pNode){

pPre = pPre->right;

}

if (pPre->right == NULL)

{

/* code */

pPre->right = pNode;

cout<val<

pNode = pNode->left;

}

else{

pPre->right = NULL;

pNode = pNode->right;

}

}

}

}

中序遍歷

中序遍歷：先訪問左孩點，然后訪問根節點，最后訪問右孩子。

所以，上面遍歷的結果是：DEAGHCS。

下面，我們來看看具體代碼實現

1.遞歸實現

void InOrder(TreeNode *root){

if (root==NULL)

return;

InOrder(root->left);

cout<val<

InOrder(root->right);

}

2.使用輔助棧

實現思路：

初始化一個二叉樹結點pNode指向根結點；

若pNode非空，那么就把pNode入棧，并把pNode變為其左孩子；(直到最左邊的結點)

若pNode為空，彈出棧頂的結點，并訪問該結點，將pNode指向其右孩子(訪問最左邊的結點，并遍歷其右子樹)

具體實現：

void InOrder(TreeNode *root){

if (root==NULL)

{

return;

}

stack stk;

TreeNode *pNode = root;

while(pNode!=NULL || !stk.empty()){

if (pNode != NULL)

{

stk.push(pNode);

pNode = pNode->left;

}

else{

pNode = stk.pop();

stk.pop();

cout<val<

pNode = pNode->right;

}

}

}

3.Morris遍歷

實現思路：

1.如果當前節點pNode的左孩子為空，那么輸出該節點，并把該節點的右孩子作為當前節點

2.如果當前節點pNode的左孩子非空，那么找出該節點在中序遍歷的前驅結點prev

當第一次訪問該前驅結點prev時，其右孩子必定為空，那么就將其右孩子設置為當前結點，以便根據這個指針返回到當前結點pNode中，并將當前結點pNode設置為其左孩子；

當該前驅結點pPre的右孩子為當前結點，那么就輸出當前結點，并把前驅結點的右孩子設置為空(恢復樹的結構)，將當前結點更新為當前結點的右孩子；

3.重復以上兩步，直到當前結點為空。

具體實現：

void InOrder(TreeNode *root){

if (root == NULL)

return;

TreeNode* pNode = root;

while(pNode != NULL){

if (pNode->left == NULL)

{

cout<val<

pNode = pNode->right;

}

else{

TreeNode* pPre = pNode->left;

while(pPre->right != NULL && pPre->right != pNode){

pPre = pPre->right;

}

if (pPre->right == NULL)

{

/* code */

pPre->right = pNode;

pNode = pNode->left;

}

else{

pPre->right = NULL;

cout<val<

pNode = pNode->right;

}

}

}

}

后序遍歷

后序遍歷：先訪問左孩子，然后訪問右孩子，最后訪問根節點。

所以，上面遍歷的結果是：DAEHSCG。

下面，我們來看看具體代碼實現：

1.遞歸實現

void PostOrder(TreeNode *root){

if (root==NULL)

return;

PostOrder(root->left);

PostOrder(root->right);

cout<val<

}

2.使用輔助棧

void postOrder(TreeNode *root) {

if(root == NULL)

return;

stack stk;

stk.push(root);

TreeNode *prev = NULL;

while(!stk.empty()) {

TreeNode *pNode = stk.top();

if(!prev || prev->left == pNode || prev->right == pNode) { // traverse down

if(pNode->left)

stk.push(pNode->left);

else if(pNode->right)

stk.push(pNode->right);

/* else {

cout << pNode->val << endl;

stk.pop();

}

*/

}

else if(pNode->left == prev) { // traverse up from left

if(pNode->right)

stk.push(pNode->right);

}

/* else if(pNode->right == prev) { // traverse up from right

cout << pNode->val << endl;

stk.pop();

}

*/

else {

cout << pNode->val << endl;

stk.pop();

}

prev = pNode;

}

}

雙輔助棧實現思路：

設置兩個棧stk, stk2；

將根結點壓入第一個棧stk；

彈出stk棧頂的結點，并把該結點壓入第二個棧stk2；

將當前結點的左孩子和右孩子先后分別入棧stk；

當所有元素都壓入stk2后，依次彈出stk2的棧頂結點，并訪問之。

第一個棧的入棧順序是：根結點，左孩子和右孩子；于是，壓入第二個棧的順序是：根結點，右孩子和左孩子。

因此，彈出的順序就是：左孩子，右孩子和根結點。

void PostOrder2(TreeNode *root){ //兩個棧實現

if (root == NULL)

return;

stack stk,stk2;

stk.push(root);

while(!stk.empty()){

TreeNode* pNode = stk.top();

stk.pop();

stk2.push(pNode);// 將根節點壓棧

if (pNode->left != NULL) // 如果左孩子不為空，則壓棧

{

stk.push(pNode->left);

}

if (pNode->right != NULL) // 如果左孩子不為空，則壓棧

{

stk.push(pNode->right);

}

}

while(!stk2.empty()){

cout<val<

stk2.pop();

}

}

3.Morris遍歷實現

實現思路：

1.先建立一個臨時結點dummy，并令其左孩子為根結點root，將當前結點設置為dummy；

2.如果當前結點的左孩子為空，則將其右孩子作為當前結點；

3.如果當前結點的左孩子不為空，則找到其在中序遍歷中的前驅結點，

-如果前驅結點的右孩子為空，將它的右孩子設置為當前結點，將當前結點更新為當前結點的左孩子；

-如果前驅結點的右孩子為當前結點，倒序輸出從當前結點的左孩子到該前驅結點這條路徑上所有的結點。將前驅結點的右孩子設置為空，將當前結點更新為當前結點的右孩子。

4.重復以上過程，直到當前結點為空。

具體實現：

void reverse(TreeNode* p1,TreeNode *p2){

if (p1 == p2)

return;

TreeNode* x = p1;

TreeNode* y = p1->right;

while(true){

TreeNode* tmp = y->right;

y->right = x;

x = y;

y = tmp;

if (x == p2)

break;

}

}

void printReverse(TreeNode* p1,TreeNode *p2){

reverse(p1,p2);

TreeNode* pNode = p2;

while(true){

cout<val<

if (pNode == p1)

break;

pNode = pNode->right;

}

reverse(p2,p1);

}

void PostOrder3(TreeNode* root){

if(root == NULL)

return;

TreeNode *dummy = new TreeNode(-1);

dummy->left = root;

TreeNode *pNode = dummy;

while(pNode != NULL) {

if(pNode->left == NULL)

pNode = pNode->right;

else {

TreeNode *pPrev = pNode->left;

while(pPrev->right != NULL && pPrev->right != pNode)

pPrev = pPrev->right;

if(pPrev->right == NULL) {

pPrev->right = pNode;

pNode = pNode->left;

}

else {

printReverse(pNode->left, pPrev);

pPrev->right = NULL;

pNode = pNode->right;

}

}

}

}

總結

上述三種遍歷方式時間復雜度和空間復雜度分析：

1.遞歸遍歷和非遞歸遍歷 時間復雜度0(n) 空間復雜度O(n)

2.Morris遍歷 時間復雜度0(n) 空間復雜度O(1)

以上就是本文的全部內容，希望對大家的學習有所幫助，也希望大家多多支持。