圖文并茂重新認識下遞歸

大家好，我是若川。持續組織了5個月源碼共讀活動，感興趣的可以點此加我微信 ruochuan12?參與，每周大家一起學習200行左右的源碼，共同進步。同時極力推薦訂閱我寫的《學習源碼整體架構系列》?包含20余篇源碼文章。

對于大部分前端(包括我)接觸到遞歸的時候就是學函數的時候，對于遞歸的認知就是函數自己調用自己，然后給函數定義一個出口，通過這個函數將一件的事情拆分成同類型的小事情。但你會發現你寫的遞歸情況很少，因為很多情況下遞歸是可以用循環去實現同樣的效果，那對于遞歸具體使用場景，什么時候需要用遞歸，就是本文主要想探討的話題。

遞歸只能去解決樹形結構的問題嗎？

對于很少使用遞歸來解決問題的很容易就會把遞歸想成只有樹形情況才能使用遞歸，下面我們先通過解決樹形情況深入了解遞歸能解決哪些場景的問題以及除了樹形結構的數據，它還能處理什么問題？

「問題一」：獲取根節點名稱

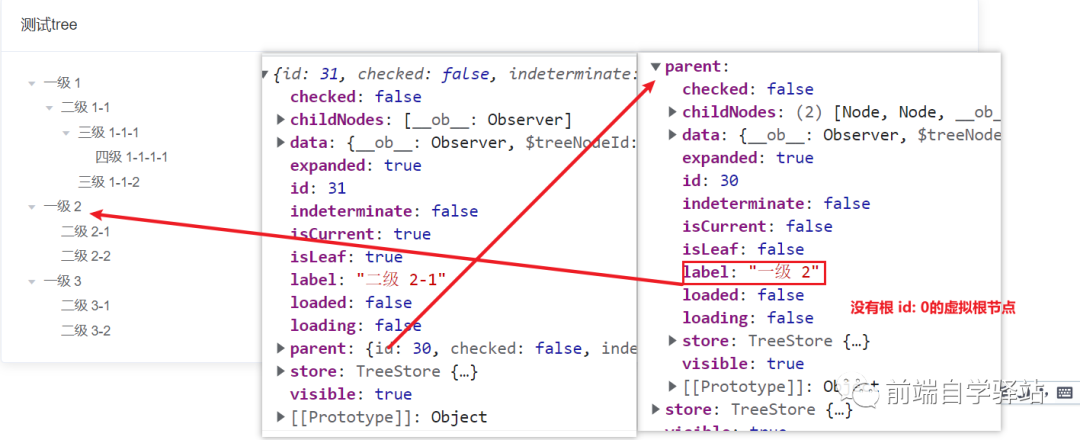
點擊當前節點獲取根級節點的名稱

這里用element的el-tree組件來做測試，根級節點不包括tree中的虛擬根節點，指的是數據的根節點

這就是虛擬根節點

實現的效果是這樣的

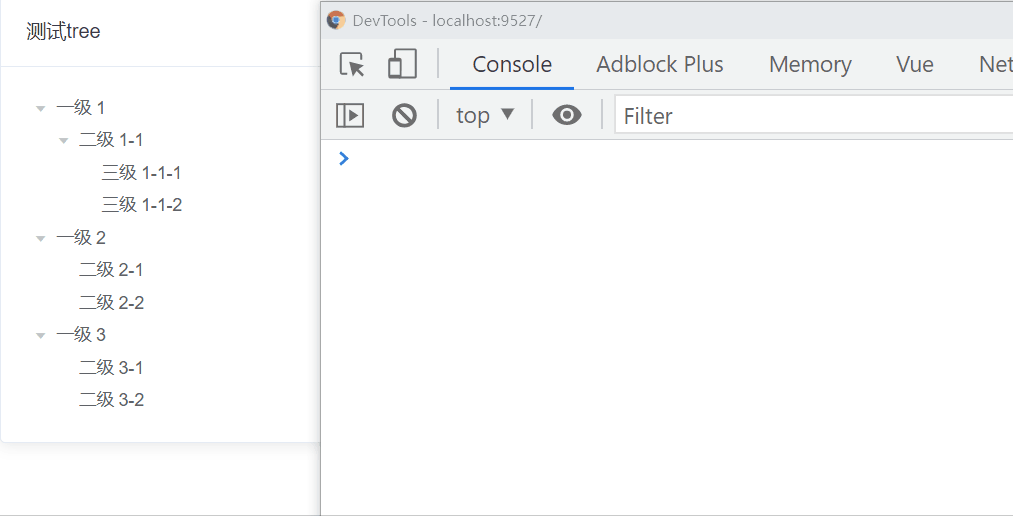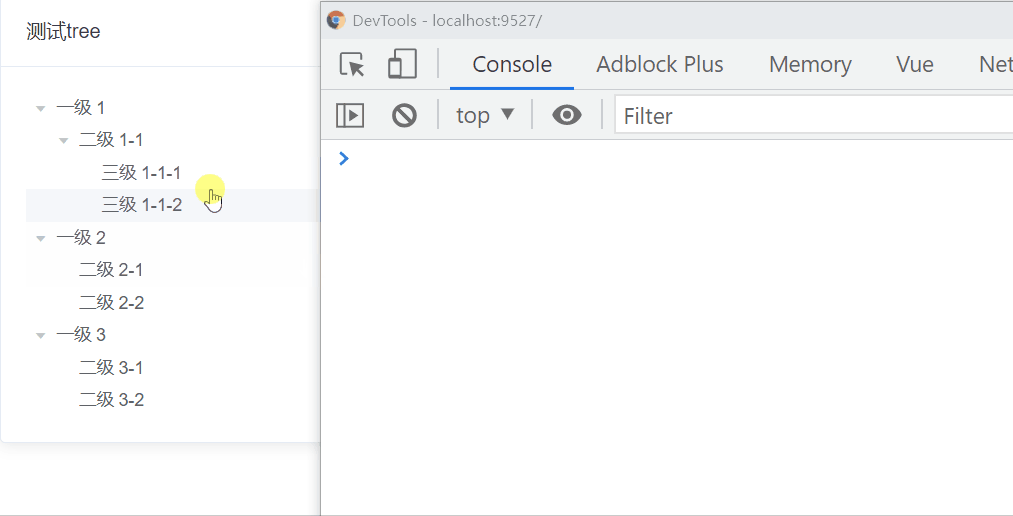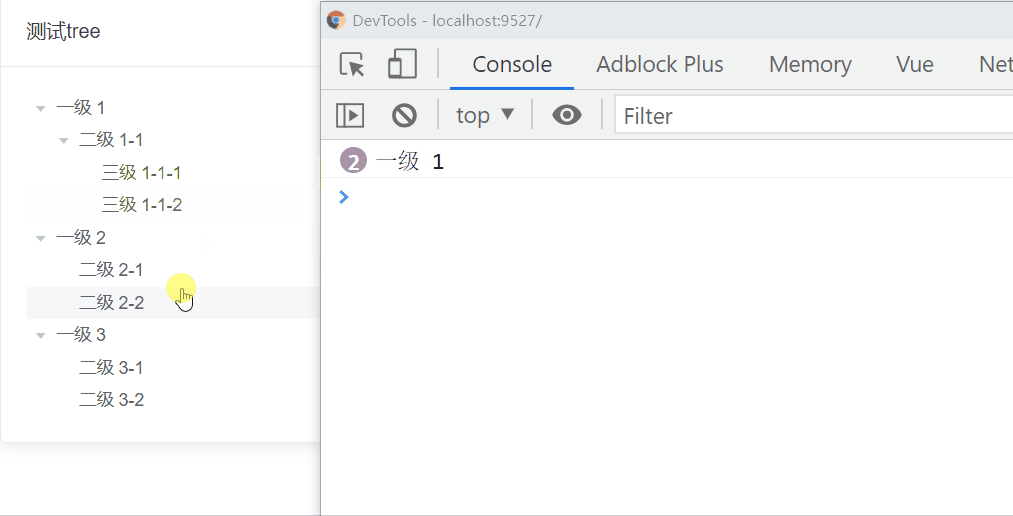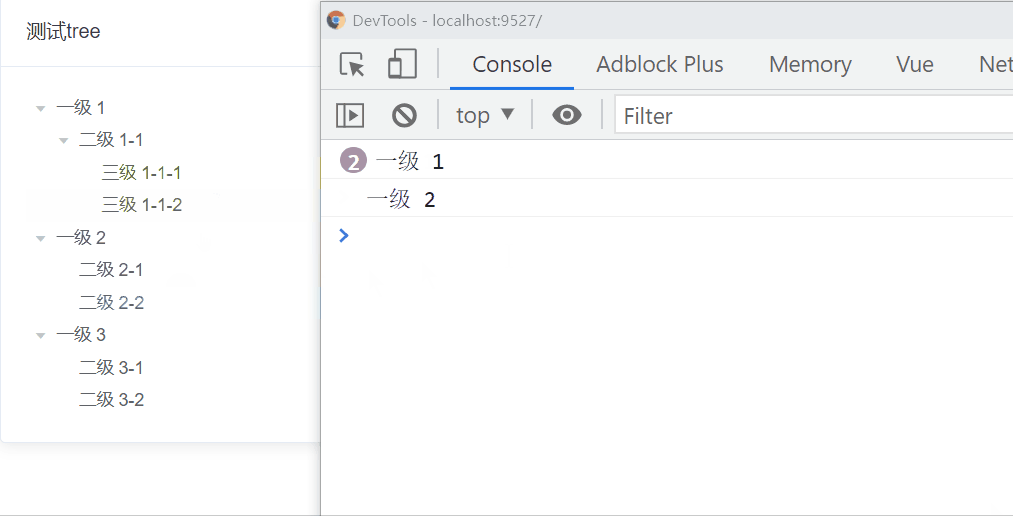
這個需求很簡單，我們很容易就想到了遞歸，為什么?

獲取根級：不停的獲取當前節點的上級，至到沒有上級就是根級
遞歸出口條件：通過node.parent或者node.level
遞歸中變化的狀態值：node.parent

getRootNodeName(node)?{if?(!node)?returnif?(node.level?===?1)?{return?node.label}return?this.getRootNodeName(node.parent)
}

通過上面三個條件我們實現了這個遞歸函數，這里需要注意的是遞歸中變化的狀態值，這個是整個遞歸中最難理解也最重要的部分，后文會展開來講

這種遞歸其實很易就能寫出來，循環就只能實現一樣的效果

getRootNodeName(node)?{if?(!node)?returnwhile?(node.level?>?1)?{node?=?node.parent}return?node.label
}

「問題二」：獲取當前節點所在樹的指定層級節點

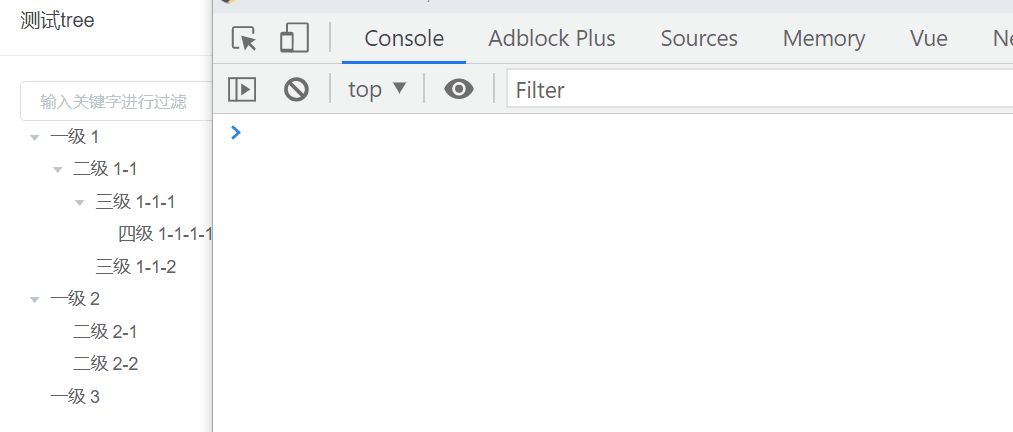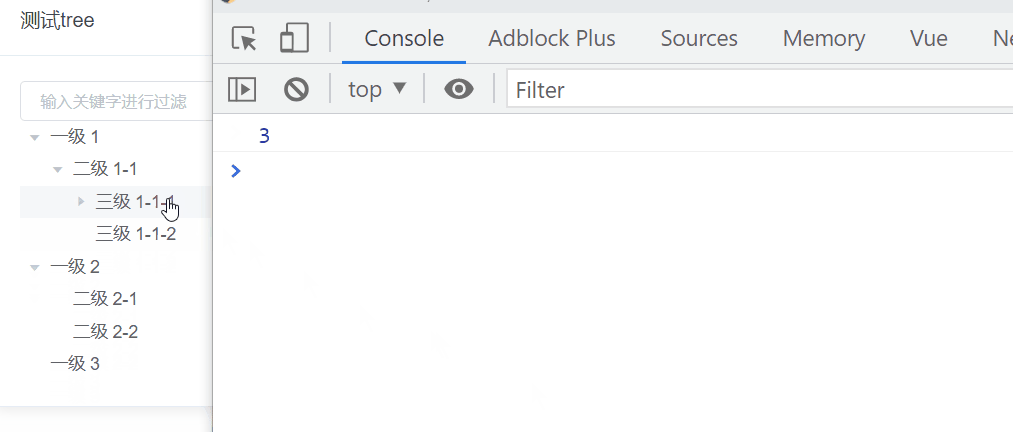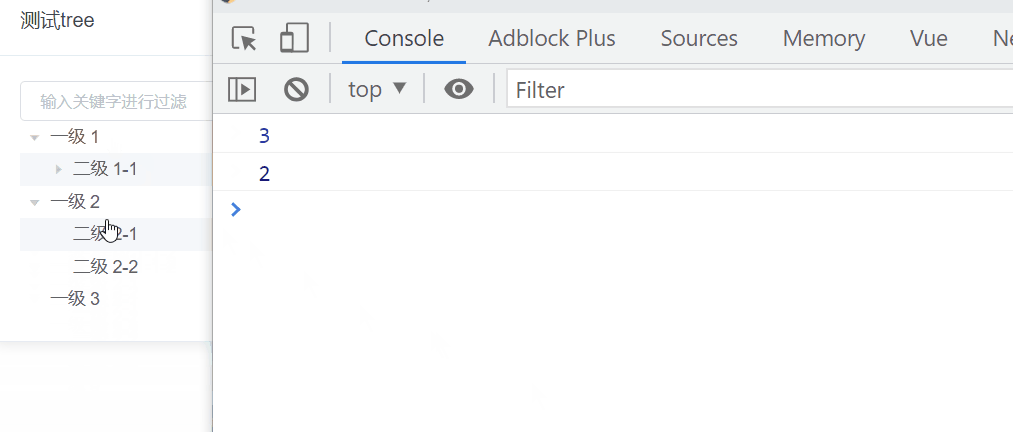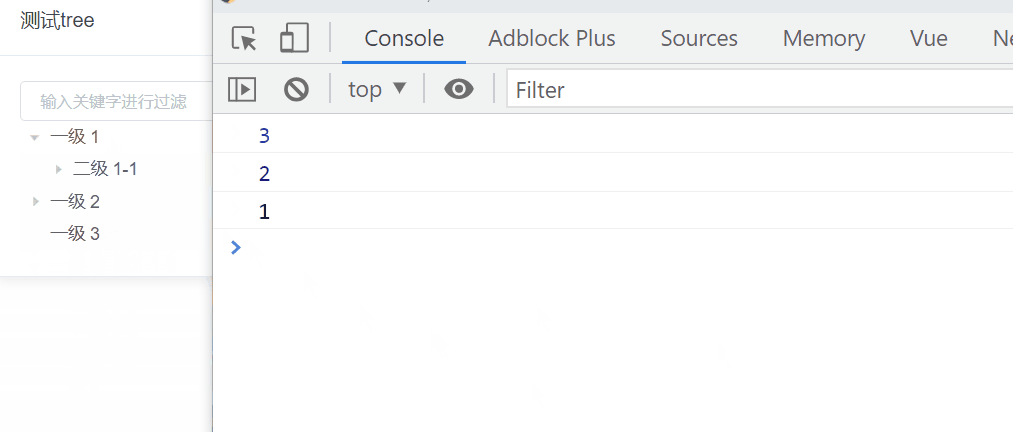
這里有還有個約束條件，node節點中沒有level屬性了，只有parent屬性指向節點的父節點，這里為了更好的表達，我們把node節點的中的虛擬根節點去除。

我們要實現這樣的效果：點擊當前節點獲取當前節點所在的層級

遞歸實現

getNodeLevel(node)?{if?(!node.parent)?return?1return?this.getNodeLevel(node.parent)?+?1
}

當前這個遞歸函數主要實現思路就是在不停的遞進，當node.parent不存在就說明當前節點是一級節點，然后在回溯的過程中在上級節點的層級 + 1 = 當前節點層級

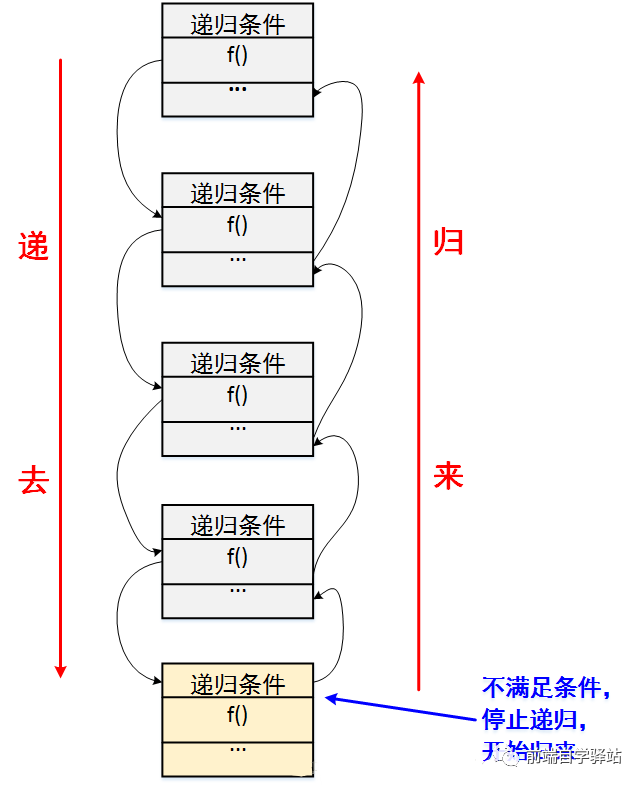
遞歸：你打開面前這扇門，看到屋里面還有一扇門。你走過去，發現手中的鑰匙還可以打開它，你推開門，發現里面還有一扇門，你繼續打開它。若干次之后，你打開面前的門后，發現只有一間屋子，沒有門了。然后，你開始原路返回，每走回一間屋子，你數一次，走到入口的時候，你可以回答出你用這把鑰匙打開了幾扇門。

循環實現

getNodeLevel(node)?{let?n?=?1let?p?=?nodewhile?(p.parent)?{p?=?p.parentn++}return?n
}

循環：你打開面前這扇門，看到屋里面還有一扇門。你走過去，發現手中的鑰匙還可以打開它，你推開門，發現里面還有一扇門（若前面兩扇門都一樣，那么這扇門和前兩扇門也一樣；如果第二扇門比第一扇門小，那么這扇門也比第二扇門小，你繼續打開這扇門，一直這樣繼續下去直到打開所有的門。但是，入口處的人始終等不到你回去告訴他答案

上面兩段話其實就很好的說出了遞歸和循環之間的差別，就是因為循環沒有回溯的過程，我們當前的循環就不得不存儲每個遞歸的狀態值數據

「問題三」: 樹節點的過濾

有人可能會問樹節點的過濾這個在el-tree的用例中不就有嗎？但是那個并不能解決我們實際場景的問題，舉個例子來看下

<el-tree...:filter-node-method="filterNode"
/><script>
export default {methods: {filterNode(value, data) {if (!value) return truereturn data.label.indexOf(value) !== -1},}
}
</script>

存在的問題

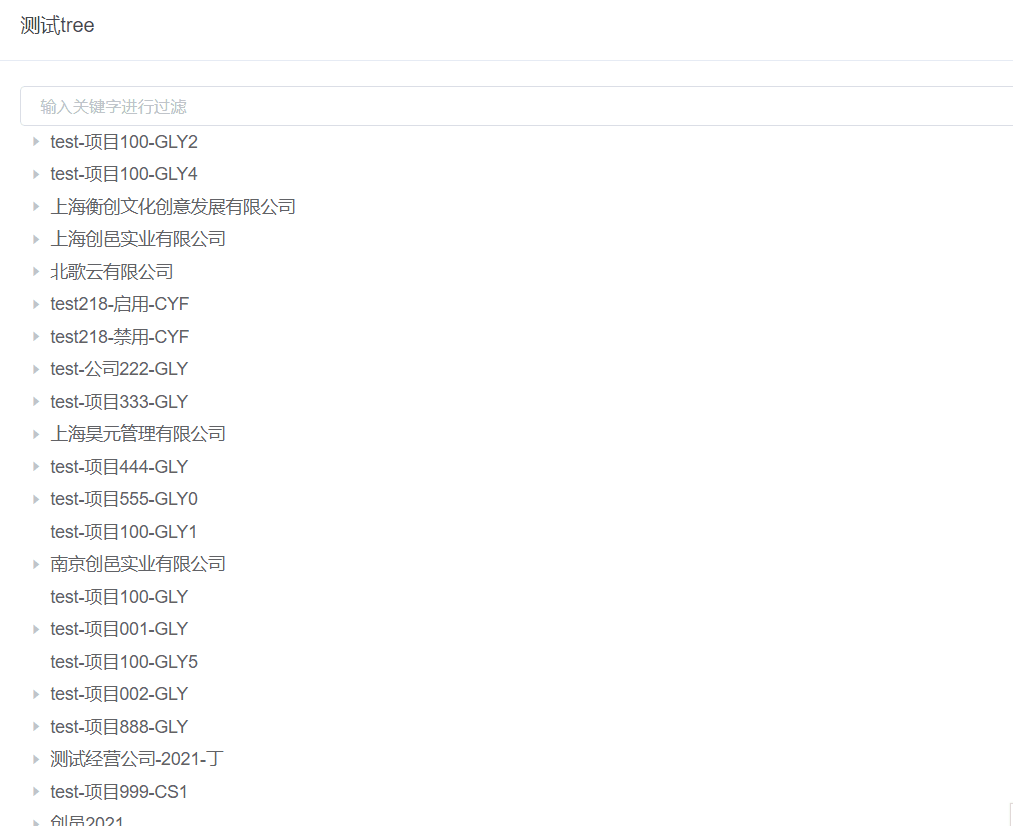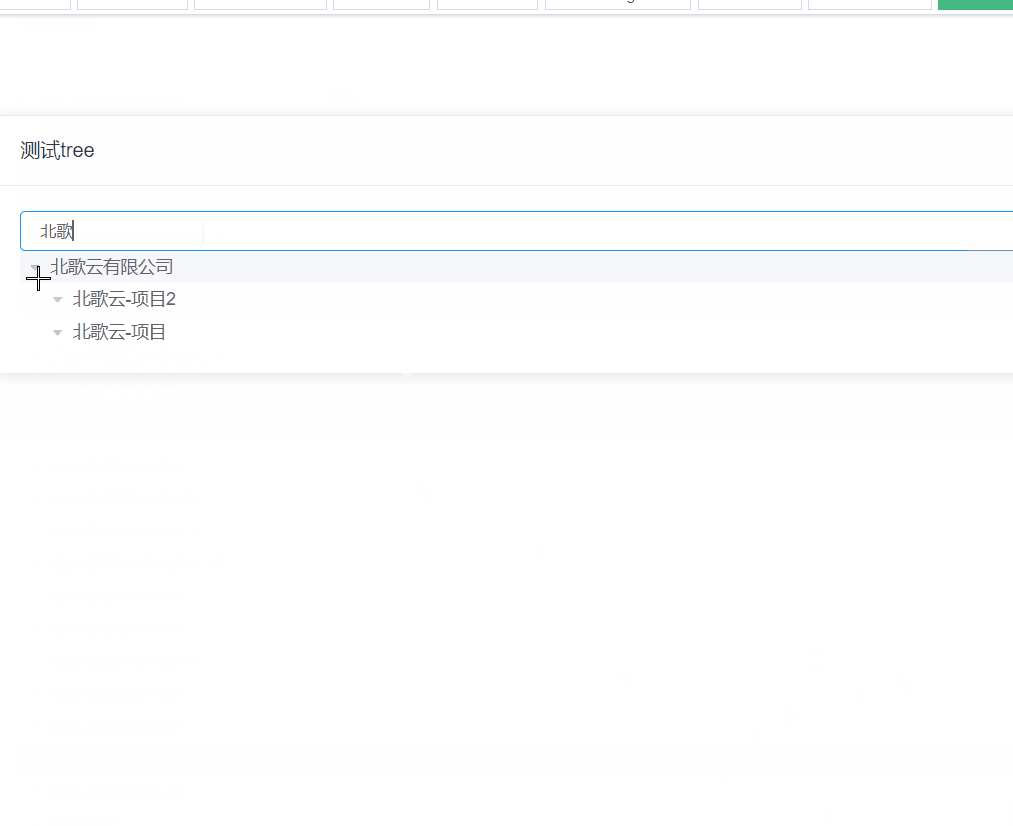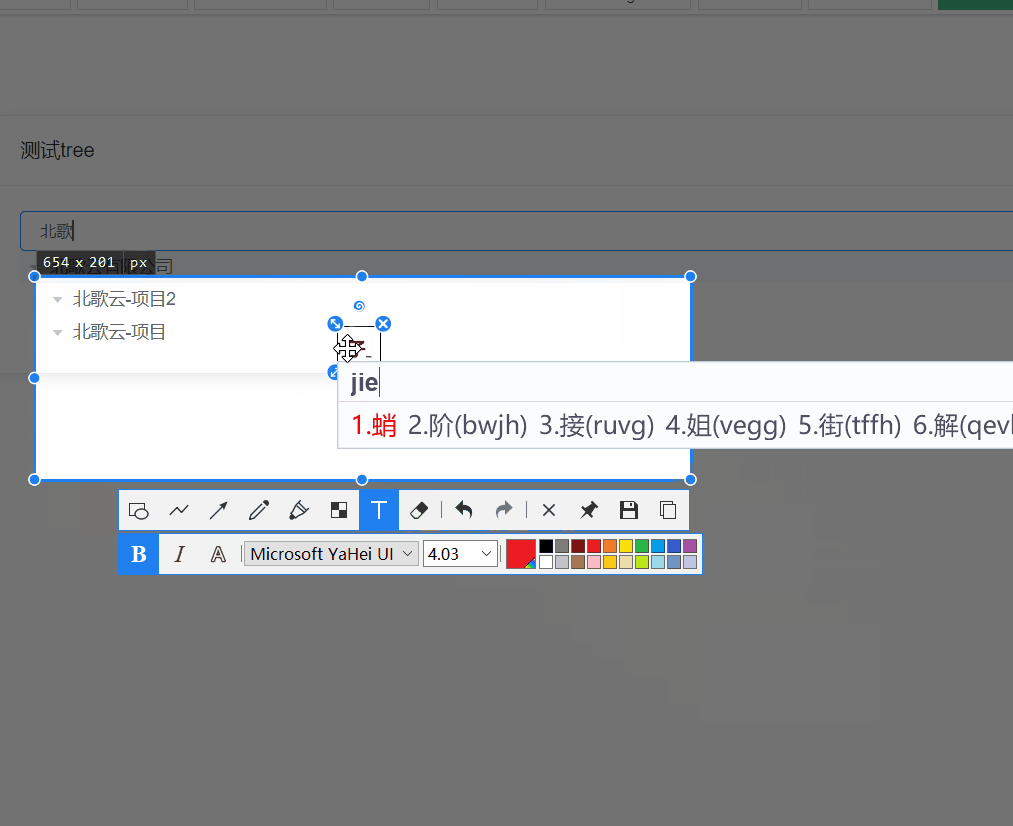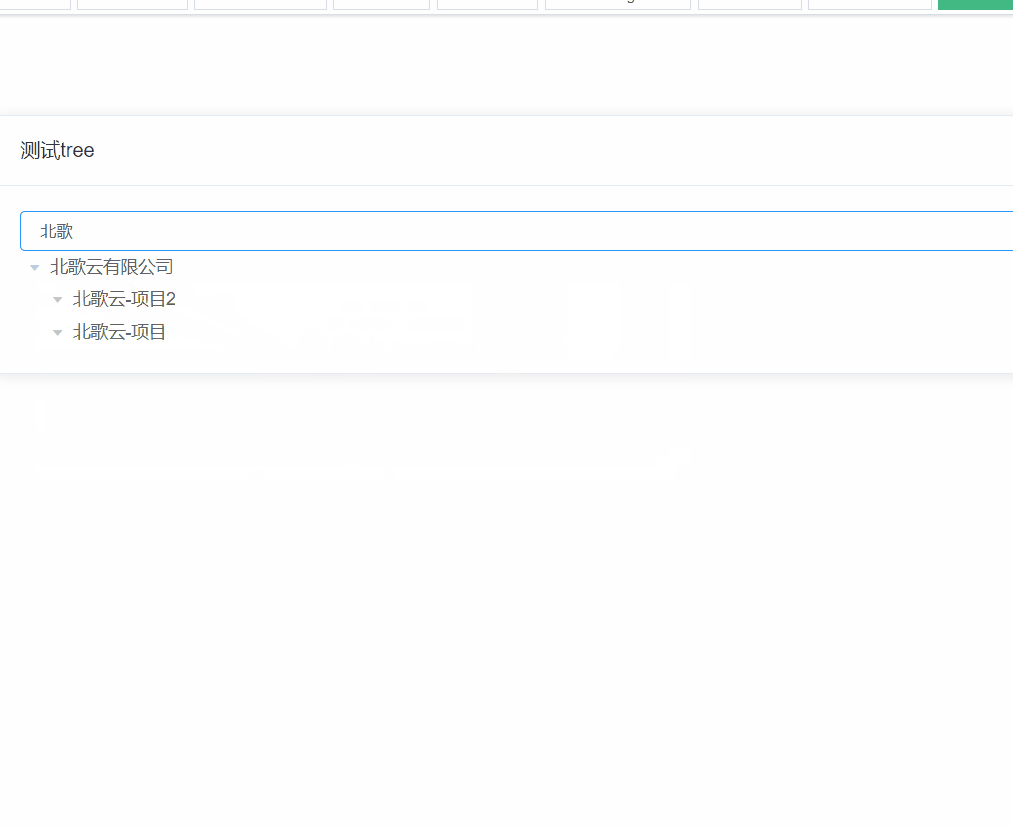
當前的過濾只是通過label包含的方式把不符合的節點全都過濾掉了，而我們想要的效果應該是過濾不符合條件的分支，如果符合當前層級符合條件那它的下級就不應該過濾掉

遞歸實現

methods:?{filterNodeMethod(value,?data,?node)?{if?(!value)?{return?true}return?this.deepfilterChildNode(value,?node)},deepfilterChildNode(value,?node)?{if?(node.level?===?1)?return?falseconst?{?filterNodeByIndexOf,?deepfilterChildNode?}?=?thisif?(filterNodeByIndexOf(node.label,?value))?{return?true}return?deepfilterChildNode(value,?node.parent)},filterNodeByIndexOf(label,?value)?{return?label.indexOf(value)?!==?-1}
}

循環實現

主要實現函數就是deepfilterChildNode, 接著再用循環來實現下同步的效果

methods:?{deepfilterChildNode(value,?node)?{const?{?filterNodeByIndexOf?}?=?thisif?(filterNodeByIndexOf(node.label,?value))?{return?true}//?一級節點沒有父級if?(node.level?===?1)?return?false//?往上找到最大那個節點結束const?maxNode?=?1?//?多級節點父級符合條件，不要、過濾子級let?parentNode?=?node.parentwhile?(parentNode.level?>?maxNode)?{if?(filterNodeByIndexOf(parentNode.label,?value))?{return?true}parentNode?=?parentNode.parent}//?當前節點的最大父節點都沒找到return?false},
}

「問題四」：實現instanceof

作用：判斷右邊構造函數的原型對象是否存在于左邊對象的原型鏈上
原理：左側的原型鏈中存在右側的原型對象

左側必須是對象

1?instaceof?Number?//?false
Number(1)?instaceof?Number?//?false
new?Number(1)?instaceof?Number?//?true

右側必須是構造函數

let?f1?=?()?=>?{};
let?f2?=?function?()?{}
class?f3?{}
obj?instanceof?f1;?//?報錯
obj?instanceof?f2?//?false
obj?instanceof?f3?//?false

左側的原型鏈中存在右側的原型對象

let?obj?=?{}
class?ctor?{}
console.log(obj?instanceof?ctor);?//?false
Object.setPrototypeOf(obj,?new?ctor)
console.log(obj?instanceof?ctor);?//?truelet?getProto?=?Object.getPrototypeOf
getProto(getProto(obj))?===?ctor.prototype?//?true

遞歸實現

function?_instaceof(obj,?ctor)?{//?左邊必須是對象if?(!(obj?&&?typeof?obj?===?'object'))?{return?false}//?獲取對象的原型鏈對象let?proto?=?Object.getPrototypeOf(obj)//?判斷對象的原型鏈對象是否是構造函數函數的原型對象return?proto?===?ctor.prototype?||?_instaceof(proto,?ctor)
}

循環實現

function?instanceOf1(obj,?ctor)?{if?(!(obj?&&?typeof?obj?===?'object'))?{return?false}let?proto?while(proto?=?Object.getPrototypeOf(obj))?{if?(Object.is(proto,?ctor.prototype))?return?trueobj?=?proto}return?false
}

「問題五」深度屬性

測試數據

let?obj?=?{a:?{b:?{c:?1,cc:?{dd:?{f:?'f?Val'}}}},data:?{v1:?'v1',v2:?'v2',v3:?'v3'}
}

獲取屬性

function?getDeepObjAttr(obj,?deepPath)?{const?deepGet?=?(o,?paths)?=>?{if?(!paths.length)?return?oreturn?deepGet(Reflect.get(o,?paths.shift()),?paths)}return?deepGet(obj,?deepPath.split('.'))
}

console.log(getDeepObjAttr(obj,?'a.b.cc.dd.f'))?//?f?Val

設置屬性

function?setDeepObjAttr(model,?deepPath,?val)?{let?paths?=?deepPath.split('.')if?(!paths.length)?return?modelconst?setDeep?=?(o,?p,?i)?=>?{if?(i?<?0)?return?olet?prop?=?p[i]//?最后一層要設定的值if?(i?===?p.length?-?1)?{Reflect.set(o,?prop,?val)}?else?{Reflect.set(o,?prop,?{...getDeepObjAttr(model,?p.slice(0,?i?+?1).join('.')),...o})Reflect.deleteProperty(o,?paths[i?+?1])}return?setDeep(o,?p,?--i)}return?Object.assign(model,setDeep({},?[...paths],?paths.length?-?1))
}

setDeepObjAttr(obj,?'a.b.c',?'2')
setDeepObjAttr(obj,?'a.b.cc.dd.f',?'f?Val21')

改變后的obj

{"a":?{"b":?{"c":?"2","cc":?{"dd":?{"f":?"f?Val21"}}}},"data":?{"v1":?"v11","v2":?"v2","v3":?"v3"}
}

這個遞歸有多個出口條件且并不是在單純的做一件類型事情，且遞歸函數中引用的自由變量(全局變量）model，遞歸過程中如果修改model，其他遞歸中的變量也會受影響

對于遞歸那些狀態值(變量)需要提取到全局，可以這樣思考

類似于盜夢空間，我手里有10塊錢，我做了第一個夢(n)，在這個夢中我花了2塊，接著又做了一個夢(n + 1), 在n+1中我還是有10塊錢，前面夢中花掉的錢并不影響我這個夢中的錢。那這個狀態值(變量)就是遞歸函數內部創建的局部變量，反之就需要把狀態值(變量)放到全局

這里同樣給出循環的實現

function?getDeepObjAttr(obj,?deepPath)?{let?paths?=?deepPath.split('.')if?(!paths.length)?return?objlet?prop,targetVal,tempObj?=?objwhile?((prop?=?paths.shift())?&&?paths.length)?{if?(!Reflect.has(tempObj,?prop))?{return}tempObj?=?tempObj[prop]}return?tempObj[prop]
}

function?setDeepObjAttr(model,?deepPath,?val)?{//?路徑let?paths?=?deepPath.split('.')//?目標值，存放符合路徑下的所有屬性let?targetVal?=?{}//?用于查找每個對象的proplet?pathsNew?=?paths.concat([])let?propfor?(let?i?=?paths.length?-?1,?j?=?i;?i?>=?0;?i--)?{prop?=?paths[i]//?最后一層要設定的值if?(i?===?j)?{targetVal[prop]?=?val}?else?if?(i?===?0)?{//?第一層需要直接替換第一個屬性const?obj?=?this.getDeepObjAttr(model,?prop);Reflect.set(model,?prop,?Object.assign({},?obj,?targetVal))}?else?{//?更新每一個層級的值(去除存起來的值)let?curDeppObj?=?getDeepObjAttr(model,?pathsNew.join('.'))//?將當前層級的值存儲起來Reflect.set(targetVal,?prop,?Object.assign({},?curDeppObj,?targetVal))//?刪除上個路徑存儲的值Reflect.deleteProperty(targetVal,?paths[i?+?1])}//?將處理過的路徑去除pathsNew.pop()}return?model
}

對于遞歸是否只能解決樹形結構的問題，還沒有給出答案，又出現了一個問題，遞歸和循環的區別？

遞歸和循環有什么區別？

通過上面的五個例子我們發現遞歸和循環都能實現，其實遞歸與循環是兩種不同的解決問題的典型思路，都具有相同的特性，即做重復任務。單從算法設計上看，遞歸和循環并無優劣之別。然而，在實際開發中，因為函數調用的開銷，遞歸常常會帶來性能問題，特別是在求解規模不確定的情況下；而循環因為沒有函數調用開銷，所以效率會比遞歸高。

插一句，求解規模不確定還包含隱示的數據規模很大，但前端頁面很少會碰到處理數據規模特別大的情況，所以用遞歸也沒啥問題

相同點：

將大事件拆分成小事情即**重復任務 **（循環、遞歸調用）
處理過程中將狀態值變換即狀態展開

區別：

如果使用循環我們就得建立堆棧來替代系統棧保存處理當前狀態的內容(變量)

再次認識遞歸

let?arr?=?[1,?2,?3,?4,?5,?6]function?logArr(arr)?{for?(let?i?=?0;?i?<?arr.length;?i++)?{console.log(arr[i]);}
}
logArr(arr)

讓你依次打印輸出中的每一項，這個能用遞歸實現嗎？？？

先想想

答案是肯定可以

function?logArr(arr)?{const?dfs?=?(idx)?=>?{if?(idx?===?arr.length)?returnconsole.log(arr[idx]);dfs(idx?+?1)}dfs(0)
}

斐波納契數列

斐波納契數列，指的是這樣一個數列：1、1、2、3、5、8、13、21，簡單來講就是從第二個數之后的每個數是前兩個數之和： F0=0，F1=1，Fn=F(n-1)+F(n-2)（n>=2）

遞歸求解

function?fibonacci(n)?{//?遞歸終止條件if?(n?<=?2)?{return?1}//?相同重復邏輯，縮小問題的規模return?fibonacci(n?-?1)?+?fibonacci(n?-?2)
}

fibonacci(5)

狀態展開生成樹

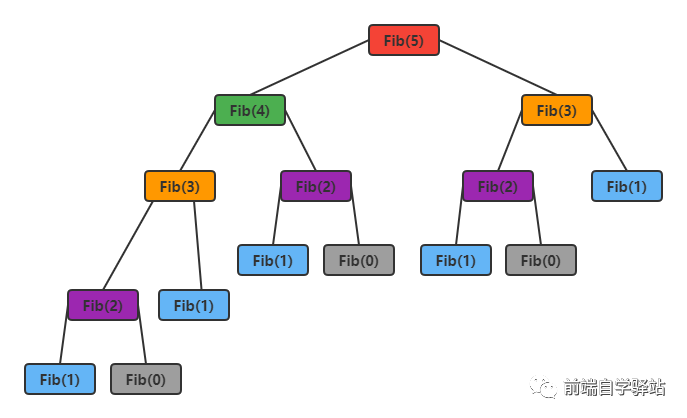
這里面包含了許多重復計算，計算fib(5)時

1次fib(4)
2次fib(3)
3次fib(2)
5次fib(1)?
3次fib(0)

像這種重復的計算就相當于相同的分支，在dfs(深度優先搜索)中有個很重要的操作叫做剪枝; 在當前遞歸的實現中那些重復的計算我們可以進行緩存當后面出現重復計算就不再調用，也算是剪枝，這對于遞歸是很大的性能優化。

//?創建一個空對象,作為緩存的容器
let?cache?=?{};
function?fibonacci(n)?{if?(n?===?1?||?n?===?2)?{return?1;}if?(cache[n])?{return?cache[n];}return?cache[n]?=?fibonacci(n?-?1)?+?fibonacci(n?-?2);
}

還有一種緩存的方案，在遞歸的過程中進行計算，回溯的時候把最后的結果返回

function?fibonacci(n,?cur?=?0,?next?=?1)?{if(n?==?0)?return?0;if(n?==?1)?return?next;?return?fibonacci(n?-?1,?next,?cur?+?next);
}

循環求解

function?fibonacci(n)?{if?(n?<=?2)?return?1//?維護"棧"的狀態值,以便狀態回溯let?first?=?1//?維護"棧"的狀態值,以便狀態回溯let?second?=?1let?ret?=?0n?-=?2while?(n--)?{//?當前數?=?前一個數?+?前兩個數ret?=?first?+?secondfirst?=?secondsecond?=?ret}return?ret
}

現在可以回答第一個問題了，遞歸不是只能去解決樹形數據結構和明顯的上下級關系的數據，對這種情況的數據是非常符合遞歸的定義所以我們很容易能想像出來，像斐波納契數列、階乘、楊輝三角..., 這種通過遞推可以求解的方式也可以用遞歸，通過遞歸過程中變化狀態值來求解答案。

二分查找

循環實現

function?binarySearch(nums,?target)?{let?l?=?0let?r?=?nums.length?-?1let?midwhile?(l?<=?r)?{mid?=?(l?+?r)?>>?1if?(nums[mid]?===?target)?{return?mid}?else?if?(nums[mid]?>?target)?{r?=?mid?-?1}?else?{l?=?mid?+?1}}return?-1
}

遞歸實現

變換狀態值，狀態展開生成樹

function?binarySearch(nums,?target,?l?=?0,?r?=?nums.length?-?1)?{let?midwhile?(l?<=?r)?{mid?=?(l?+?r)?>>?1if?(nums[mid]?===?target)?{return?mid}?else?if?(nums[mid]?>?target)?{return?binarySearch(nums,?target,?l,?mid?-?1)}?else?{return?binarySearch(nums,?target,?mid?+?1,?r)}}return?-1
}

算法中遞歸的應用

在算法中對于遞歸的應用場景特別特別多，dfs：回溯、二叉樹遍歷、翻轉、路徑總和...，把以上這些類型的題用遞歸刷幾題，對于遞歸就會有更深的認知和理解，后面碰到的需求如果可以用遞歸解，自然你就能想到遞歸。

現在給出一些遞歸可解的leetcode題，并不是說去學算法刷題，這里的目的是做這些題可以讓我們對于用遞歸有更深入的了解，遞歸用的不太多的可能需要花點時間，全都掌握之后對自己也是個提升

二叉樹遍歷

二叉樹有三種遍歷方式：

前序遍歷：根、左、右
中序遍歷：左、根、右
后續遍歷：左、右、根

前序遍歷

leetcode144. 二叉樹的前序遍歷

/***?@param?{TreeNode}?root*?@return?{number[]}*/
var?preorderTraversal?=?function(root)?{let?ans?=?[]const?preIterator?=?(root)?=>?{if?(!root)?returnans.push(root.val)preIterator(root.left)preIterator(root.right)}preIterator(root)return?ans
}

中序遍歷

leetcode94. 二叉樹的中序遍歷

/***?@param?{TreeNode}?root*?@return?{number[]}*/
var?inorderTraversal?=?function(root)?{let?ans?=?[]const?inIterator?=?(root)?=>?{if?(!root)?returninIterator(root.left)ans.push(root.val)inIterator(root.right)}inIterator(root)return?ans
};

后序遍歷

leetcode145. 二叉樹的后序遍歷

/***?@param?{TreeNode}?root*?@return?{number[]}*/
var?postorderTraversal?=?function(root)?{let?ans?=?[]const?postIterator?=?(root)?=>?{if?(!root)?returnif?(!postIterator(root.left))?{if?(!postIterator(root.right))?{ans.push(root.val)}}}postIterator(root)return?ans
};

路徑總和

leetcode112. 路徑總和

var?hasPathSum?=?function?(root,?targetSum)?{if?(!root)?return?falsetargetSum?=?targetSum?-?root.val//?當前節點是葉子節點if?(!root.left?&&?!root.right)?{//?如果當前節點剛好能符合所有ragetSum,?表示當前節點就是目標節點return?targetSum?===?0}return?hasPathSum(root.left,?targetSum)?||?hasPathSum(root.right,?targetSum)
};

leetcode113. 路徑總和 II

/***?@param?{TreeNode}?root*?@param?{number}?targetSum*?@return?{number[][]}*/
var?pathSum?=?function?(root,?targetSum)?{let?ans?=?[]const?dfs?=?(root,?targetSum,?temp?=?[])?=>?{if?(!root)?returntemp.push(root.val)targetSum?-=?root.valif?(!root.left?&&?!root.right?&&?targetSum?===?0)?{ans.push([...temp])}dfs(root.left,?targetSum,?temp)dfs(root.right,?targetSum,?temp)temp.pop()}dfs(root,?targetSum)return?ans
};

回溯

leetcode39. 組合總和

/***?@param?{number[]}?candidates*?@param?{number}?target*?@return?{number[][]}*/var?combinationSum?=?function?(candidates,?target)?{const?ans?=?[]const?dfs?=?(idx,?target,?temp?=?[])?=>?{if?(idx?===?candidates.length)?returnif?(target?<?0)?returnif?(target?===?0)?{ans.push([...temp])temp?=?[]return}temp.push(candidates[idx])dfs(idx,?target?-?candidates[idx],?temp)temp.pop()dfs(idx?+?1,?target,?temp)}dfs(0,?target)return?ans
};

寫在最后

業精于勤，荒于嬉

如果文章中有那塊寫的不太好或有問題歡迎大家指出，我也會在后面的文章不停修改。也希望自己進步的同時能跟你們一起成長。喜歡我文章的朋友們也可以關注一下，我會很感激第一批關注我的人。此時，年輕的我和你，輕裝上陣；而后，富裕的你和我，滿載而歸。

·················?若川簡介?·················

你好，我是若川，畢業于江西高校。現在是一名前端開發“工程師”。寫有《學習源碼整體架構系列》20余篇，在知乎、掘金收獲超百萬閱讀。
從2014年起，每年都會寫一篇年度總結，已經寫了7篇，點擊查看年度總結。
同時，最近組織了源碼共讀活動，幫助3000+前端人學會看源碼。公眾號愿景：幫助5年內前端人走向前列。