
上篇主要介紹了幾種常用的聚類算法,首先從距離度量與性能評估出發,列舉了常見的距離計算公式與聚類評價指標,接著分別討論了K-Means、LVQ、高斯混合聚類、密度聚類以及層次聚類算法。K-Means與LVQ都試圖以類簇中心作為原型指導聚類,其中K-Means通過EM算法不斷迭代直至收斂,LVQ使用真實類標輔助聚類;高斯混合聚類采用高斯分布來描述類簇原型;密度聚類則是將一個核心對象所有密度可達的樣本形成類簇,直到所有核心對象都遍歷完;最后層次聚類是一種自底向上的樹形聚類方法,不斷合并最相近的兩個小類簇。本篇將討論機器學習常用的方法--降維與度量學習。
11、降維與度量學習
樣本的特征數稱為維數(dimensionality),當維數非常大時,也就是現在所說的“維數災難”,具體表現在:在高維情形下,數據樣本將變得十分稀疏,因為此時要滿足訓練樣本為“密采樣”的總體樣本數目是一個觸不可及的天文數字,謂可遠觀而不可褻玩焉...訓練樣本的稀疏使得其代表總體分布的能力大大減弱,從而消減了學習器的泛化能力;同時當維數很高時,計算距離也變得十分復雜,甚至連計算內積都不再容易,這也是為什么支持向量機(SVM)使用核函數**“低維計算,高維表現”**的原因。
緩解維數災難的一個重要途徑就是降維,即通過某種數學變換將原始高維空間轉變到一個低維的子空間。在這個子空間中,樣本的密度將大幅提高,同時距離計算也變得容易。這時也許會有疑問,這樣降維之后不是會丟失原始數據的一部分信息嗎?這是因為在很多實際的問題中,雖然訓練數據是高維的,但是與學習任務相關也許僅僅是其中的一個低維子空間,也稱為一個低維嵌入,例如:數據屬性中存在噪聲屬性、相似屬性或冗余屬性等,對高維數據進行降維能在一定程度上達到提煉低維優質屬性或降噪的效果。
11.1 K近鄰學習
k近鄰算法簡稱kNN(k-Nearest Neighbor),是一種經典的監督學習方法,同時也實力擔當入選數據挖掘十大算法。其工作機制十分簡單粗暴:給定某個測試樣本,kNN基于某種距離度量在訓練集中找出與其距離最近的k個帶有真實標記的訓練樣本,然后給基于這k個鄰居的真實標記來進行預測,類似于前面集成學習中所講到的基學習器結合策略:分類任務采用投票法,回歸任務則采用平均法。接下來本篇主要就kNN分類進行討論。
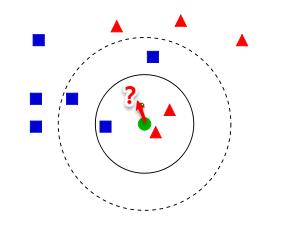
從上圖【來自Wiki】中我們可以看到,圖中有兩種類型的樣本,一類是藍色正方形,另一類是紅色三角形。而那個綠色圓形是我們待分類的樣本。基于kNN算法的思路,我們很容易得到以下結論:
- 如果K=3,那么離綠色點最近的有2個紅色三角形和1個藍色的正方形,這3個點投票,于是綠色的這個待分類點屬于紅色的三角形。
- 如果K=5,那么離綠色點最近的有2個紅色三角形和3個藍色的正方形,這5個點投票,于是綠色的這個待分類點屬于藍色的正方形。
可以發現:kNN雖然是一種監督學習方法,但是它卻沒有顯式的訓練過程,而是當有新樣本需要預測時,才來計算出最近的k個鄰居,因此kNN是一種典型的懶惰學習方法,再來回想一下樸素貝葉斯的流程,訓練的過程就是參數估計,因此樸素貝葉斯也可以懶惰式學習,此類技術在訓練階段開銷為零,待收到測試樣本后再進行計算。相應地我們稱那些一有訓練數據立馬開工的算法為“急切學習”,可見前面我們學習的大部分算法都歸屬于急切學習。
很容易看出:kNN算法的核心在于k值的選取以及距離的度量。k值選取太小,模型很容易受到噪聲數據的干擾,例如:極端地取k=1,若待分類樣本正好與一個噪聲數據距離最近,就導致了分類錯誤;若k值太大, 則在更大的鄰域內進行投票,此時模型的預測能力大大減弱,例如:極端取k=訓練樣本數,就相當于模型根本沒有學習,所有測試樣本的預測結果都是一樣的。一般地我們都通過交叉驗證法來選取一個適當的k值。
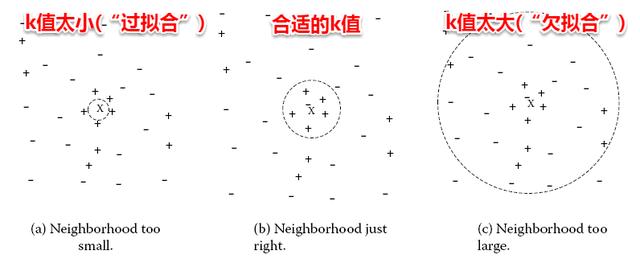
對于距離度量,不同的度量方法得到的k個近鄰不盡相同,從而對最終的投票結果產生了影響,因此選擇一個合適的距離度量方法也十分重要。在上一篇聚類算法中,在度量樣本相似性時介紹了常用的幾種距離計算方法,包括閔可夫斯基距離,曼哈頓距離,VDM等。在實際應用中,kNN的距離度量函數一般根據樣本的特性來選擇合適的距離度量,同時應對數據進行去量綱/歸一化處理來消除大量綱屬性的強權政治影響。
11.2 MDS算法
不管是使用核函數升維還是對數據降維,我們都希望原始空間樣本點之間的距離在新空間中基本保持不變,這樣才不會使得原始空間樣本之間的關系及總體分布發生較大的改變。**“多維縮放”(MDS)**正是基于這樣的思想,MDS要求原始空間樣本之間的距離在降維后的低維空間中得以保持。
假定m個樣本在原始空間中任意兩兩樣本之間的距離矩陣為D∈R(m*m),我們的目標便是獲得樣本在低維空間中的表示Z∈R(d'*m , d'< d),且任意兩個樣本在低維空間中的歐式距離等于原始空間中的距離,即||zi-zj||=Dist(ij)。因此接下來我們要做的就是根據已有的距離矩陣D來求解出降維后的坐標矩陣Z。

令降維后的樣本坐標矩陣Z被中心化,中心化是指將每個樣本向量減去整個樣本集的均值向量,故所有樣本向量求和得到一個零向量。這樣易知:矩陣B的每一列以及每一列求和均為0,因為提取公因子后都有一項為所有樣本向量的和向量。
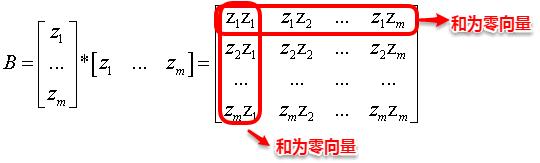
根據上面矩陣B的特征,我們很容易得到等式(2)、(3)以及(4):

這時根據(1)--(4)式我們便可以計算出bij,即bij=(1)-(2)(1/m)-(3)(1/m)+(4)*(1/(m^2)),再逐一地計算每個b(ij),就得到了降維后低維空間中的內積矩陣B(B=Z'*Z),只需對B進行特征值分解便可以得到Z。MDS的算法流程如下圖所示:

11.3 主成分分析(PCA)
不同于MDS采用距離保持的方法,主成分分析(PCA)直接通過一個線性變換,將原始空間中的樣本投影到新的低維空間中。簡單來理解這一過程便是:PCA采用一組新的基來表示樣本點,其中每一個基向量都是原來基向量的線性組合,通過使用盡可能少的新基向量來表出樣本,從而達到降維的目的。
假設使用d'個新基向量來表示原來樣本,實質上是將樣本投影到一個由d'個基向量確定的一個超平面上(即舍棄了一些維度),要用一個超平面對空間中所有高維樣本進行恰當的表達,最理想的情形是:若這些樣本點都能在超平面上表出且這些表出在超平面上都能夠很好地分散開來。但是一般使用較原空間低一些維度的超平面來做到這兩點十分不容易,因此我們退一步海闊天空,要求這個超平面應具有如下兩個性質:
- 最近重構性:樣本點到超平面的距離足夠近,即盡可能在超平面附近;
- 最大可分性:樣本點在超平面上的投影盡可能地分散開來,即投影后的坐標具有區分性。
這里十分神奇的是:最近重構性與最大可分性雖然從不同的出發點來定義優化問題中的目標函數,但最終這兩種特性得到了完全相同的優化問題:
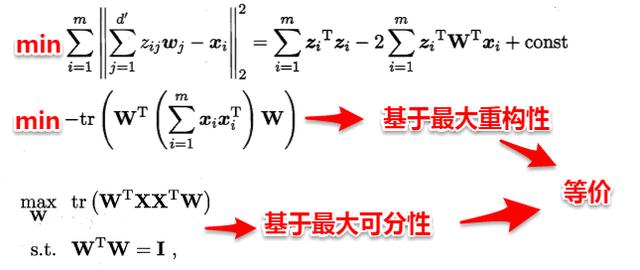
接著使用拉格朗日乘子法求解上面的優化問題,得到:

因此只需對協方差矩陣進行特征值分解即可求解出W,PCA算法的整個流程如下圖所示:

11.4 核化線性降維
說起機器學習你中有我/我中有你/水乳相融...在這里能夠得到很好的體現。正如SVM在處理非線性可分時,通過引入核函數將樣本投影到高維特征空間,接著在高維空間再對樣本點使用超平面劃分。這里也是相同的問題:若我們的樣本數據點本身就不是線性分布,那還如何使用一個超平面去近似表出呢?因此也就引入了核函數,即先將樣本映射到高維空間,再在高維空間中使用線性降維的方法。下面主要介紹**核化主成分分析(KPCA)**的思想。
若核函數的形式已知,即我們知道如何將低維的坐標變換為高維坐標,這時我們只需先將數據映射到高維特征空間,再在高維空間中運用PCA即可。但是一般情況下,我們并不知道核函數具體的映射規則,例如:Sigmoid、高斯核等,我們只知道如何計算高維空間中的樣本內積,這時就引出了KPCA的一個重要創新之處:即空間中的任一向量,都可以由該空間中的所有樣本線性表示。證明過程也十分簡單:

這樣我們便可以將高維特征空間中的投影向量wi使用所有高維樣本點線性表出,接著代入PCA的求解問題,得到:

化簡到最后一步,發現結果十分的美妙,只需對核矩陣K進行特征分解,便可以得出投影向量wi對應的系數向量α,因此選取特征值前d'大對應的特征向量便是d'個系數向量。這時對于需要降維的樣本點,只需按照以下步驟便可以求出其降維后的坐標。可以看出:KPCA在計算降維后的坐標表示時,需要與所有樣本點計算核函數值并求和,因此該算法的計算開銷十分大。

11.5 流形學習
流形學習(manifold learning)是一種借助拓撲流形概念的降維方法,流形是指在局部與歐式空間同胚的空間,即在局部與歐式空間具有相同的性質,能用歐氏距離計算樣本之間的距離。這樣即使高維空間的分布十分復雜,但是在局部上依然滿足歐式空間的性質,基于流形學習的降維正是這種**“鄰域保持”的思想。其中等度量映射(Isomap)試圖在降維前后保持鄰域內樣本之間的距離,而局部線性嵌入(LLE)則是保持鄰域內樣本之間的線性關系**,下面將分別對這兩種著名的流行學習方法進行介紹。
11.5.1 等度量映射(Isomap)
等度量映射的基本出發點是:高維空間中的直線距離具有誤導性,因為有時高維空間中的直線距離在低維空間中是不可達的。因此利用流形在局部上與歐式空間同胚的性質,可以使用近鄰距離來逼近測地線距離,即對于一個樣本點,它與近鄰內的樣本點之間是可達的,且距離使用歐式距離計算,這樣整個樣本空間就形成了一張近鄰圖,高維空間中兩個樣本之間的距離就轉為最短路徑問題。可采用著名的Dijkstra算法或Floyd算法計算最短距離,得到高維空間中任意兩點之間的距離后便可以使用MDS算法來其計算低維空間中的坐標。
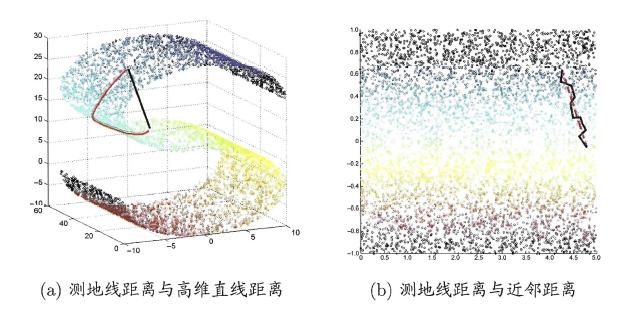
從MDS算法的描述中我們可以知道:MDS先求出了低維空間的內積矩陣B,接著使用特征值分解計算出了樣本在低維空間中的坐標,但是并沒有給出通用的投影向量w,因此對于需要降維的新樣本無從下手,書中給出的權宜之計是利用已知高/低維坐標的樣本作為訓練集學習出一個“投影器”,便可以用高維坐標預測出低維坐標。Isomap算法流程如下圖:

對于近鄰圖的構建,常用的有兩種方法:一種是指定近鄰點個數,像kNN一樣選取k個最近的鄰居;另一種是指定鄰域半徑,距離小于該閾值的被認為是它的近鄰點。但兩種方法均會出現下面的問題:
若鄰域范圍指定過大,則會造成“短路問題”,即本身距離很遠卻成了近鄰,將距離近的那些樣本扼殺在搖籃。 若鄰域范圍指定過小,則會造成“斷路問題”,即有些樣本點無法可達了,整個世界村被劃分為互不可達的小部落。
11.5.2 局部線性嵌入(LLE)
不同于Isomap算法去保持鄰域距離,LLE算法試圖去保持鄰域內的線性關系,假定樣本xi的坐標可以通過它的鄰域樣本線性表出:
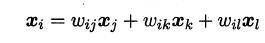
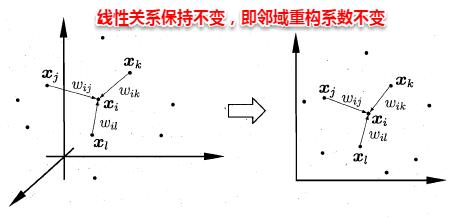
LLE算法分為兩步走,首先第一步根據近鄰關系計算出所有樣本的鄰域重構系數w:
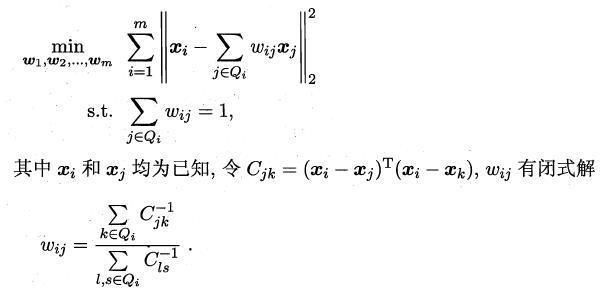
接著根據鄰域重構系數不變,去求解低維坐標:
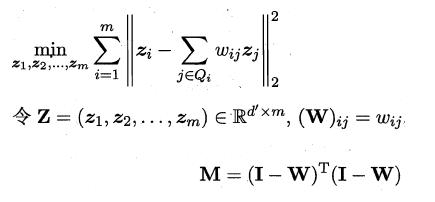
這樣利用矩陣M,優化問題可以重寫為:

M特征值分解后最小的d'個特征值對應的特征向量組成Z,LLE算法的具體流程如下圖所示:

11.6 度量學習
本篇一開始就提到維數災難,即在高維空間進行機器學習任務遇到樣本稀疏、距離難計算等諸多的問題,因此前面討論的降維方法都試圖將原空間投影到一個合適的低維空間中,接著在低維空間進行學習任務從而產生較好的性能。事實上,不管高維空間還是低維空間都潛在對應著一個距離度量,那可不可以直接學習出一個距離度量來等效降維呢?例如:咱們就按照降維后的方式來進行距離的計算,這便是度量學習的初衷。
首先要學習出距離度量必須先定義一個合適的距離度量形式。對兩個樣本xi與xj,它們之間的平方歐式距離為:
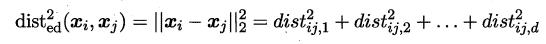
若各個屬性重要程度不一樣即都有一個權重,則得到加權的平方歐式距離:
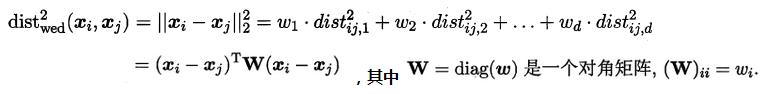
此時各個屬性之間都是相互獨立無關的,但現實中往往會存在屬性之間有關聯的情形,例如:身高和體重,一般人越高,體重也會重一些,他們之間存在較大的相關性。這樣計算距離就不能分屬性單獨計算,于是就引入經典的馬氏距離(Mahalanobis distance):
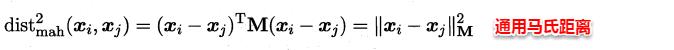
標準的馬氏距離中M是協方差矩陣的逆,馬氏距離是一種考慮屬性之間相關性且尺度無關(即無須去量綱)的距離度量。
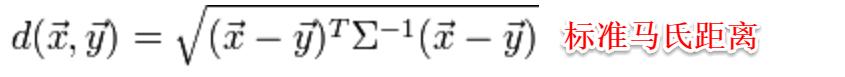
矩陣M也稱為“度量矩陣”,為保證距離度量的非負性與對稱性,M必須為(半)正定對稱矩陣,這樣就為度量學習定義好了距離度量的形式,換句話說:度量學習便是對度量矩陣進行學習。現在來回想一下前面我們接觸的機器學習不難發現:機器學習算法幾乎都是在優化目標函數,從而求解目標函數中的參數。同樣對于度量學習,也需要設置一個優化目標,書中簡要介紹了錯誤率和相似性兩種優化目標,此處限于篇幅不進行展開。
在此,降維和度量學習就介紹完畢。降維是將原高維空間嵌入到一個合適的低維子空間中,接著在低維空間中進行學習任務;度量學習則是試圖去學習出一個距離度量來等效降維的效果,兩者都是為了解決維數災難帶來的諸多問題。也許大家最后心存疑惑,那 KNN 呢?為什么一開頭就說了KNN算法,但是好像和后面沒有半毛錢關系?正是因為在降維算法中,低維子空間的維數d'通常都由人為指定,因此我們需要使用一些低開銷的學習器來選取合適的d',KNN這家伙懶到家了根本無心學習,在訓練階段開銷為零,測試階段也只是遍歷計算了距離,因此拿kNN來進行交叉驗證就十分有優勢了~同時降維后樣本密度增大同時距離計算變易,更為kNN來展示它獨特的十八般手藝提供了用武之地。
相關人工智能與異構計算的知識分享,歡迎關注我的公眾號【AI異構】



















游戲系統以及配置表...)