一、二項分布
- 二項分布來源于伯努利試驗 (事件發生概率 ) :
含義為獨立重復N次試驗后, 事件總共發生k次的概率
- 分布函數 二項分布記為
-
binopdf獲得事件共發生次的概率 -
binocdf為事件最多發生次的概率 -
binornd將生成一個服從二項分布 規模為 的隨機矩陣 - 二項分布的數字特征
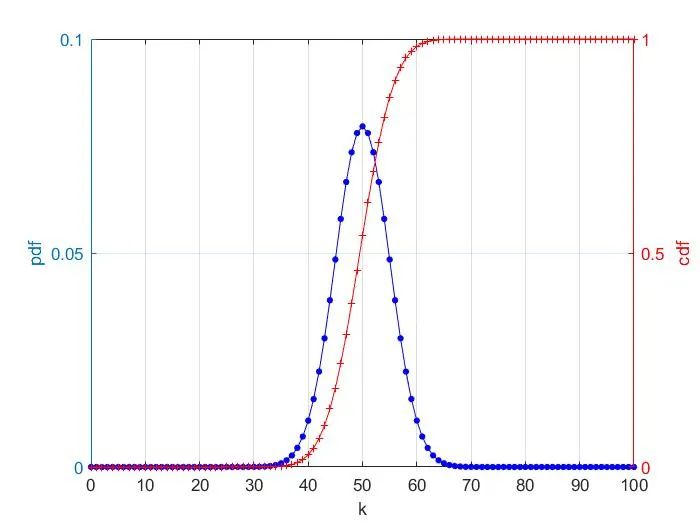
例:畫出情況下的二項分布概率特性曲線
N?=?100;?p?=?0.5;?????%?總試驗次數和單次試驗發生概率
k?=?0:N;???????%?所有可能的事件發生次數
pdf?=?binopdf(k,?N,?p);????%?繪制概率曲線
cdf?=?binocdf(k,?N,?p);????%?繪制分布曲線
h?=?plotyy(k,?pdf,?k,?cdf);???%?左右兩側不同的縱軸刻度代表兩個函數
繪制結果為:

進階繪圖技巧:
set函數的使用set(get(h(1),'Children'),'Color','b','Marker',?'.',?'MarkerSize',?13)
%?句中?get(h(1),'children')?表示獲取剛才第一條曲線繪制的所有子對象
%?然后將第一條曲線改為藍色?并且在采樣點加注實心點?不是只畫點
set(get(h(1),'Ylabel'),?'String','pdf')
%?句柄包含多個繪圖時?需要?get?出來再操作?此行改變了左側?Y?軸的標記名
set(h(2),'Ycolor',[1,?0,?0])
%?第二條曲線縱坐標軸顏色改為純紅色
set(get(h(2),'Children'),'Color','r','Marker','+','MarkerSize',4)
%?第二條曲線改為紅色并用來標注采樣點
set(get(h(2),?'Ylabel'),'String',?'cdf')
%?右側Y軸的標記名
xlabel('k')
grid?on
繪圖結果為:
二、正態分布
- 正態分布 為連續型隨機分布,期望 標準差 :
對應分布函數
normpdf) 獲得服從正態分布 的隨機變量概率密度函數在的取值。normcdf) 獲得上述正態分布隨機變量不超過的總概率normrnd將生成一個服從上述正態分 布,規模為 的隨機樣本構成的矩陣randn將生成一個服從標準正態分布 規模為 的隨機樣本構成的矩陣,事實上,我們可以利用這個矩陣可以構造任何正態分布隨機矩陣。
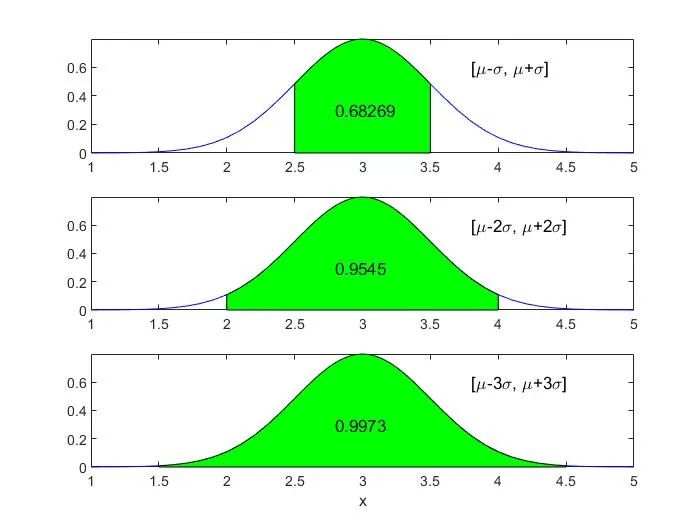
例:正態分布幾何表示
mu?=?3;?sigma?=?0.5;
x?=?mu?+?sigma*[-3:-1,1:3];?????????%?設置六個不同的采樣點
yf?=?normcdf(x,?mu,?sigma);?????????%?獲得六個點的cdf值
P?=?[yf(4)-yf(3),?yf(5)-yf(2),?yf(6)-yf(1)];????%?計算cdf的差值(內部區域面積)
xd?=?1:0.1:5;?yd?=?normpdf(xd,?mu,?sigma);?clf
for?k=1:3
???xx?=?x(4-k):sigma/10:x(3+k);
???yy?=?normpdf(xx,?mu,?sigma);
???%?對于三個不同的面積區間進行不同范圍的采樣,并獲得?pdf?函數的值
???subplot(3,?1,?k),?plot(xd,?yd,?'b');?????%?繪圖位于3行1列第k個位置
???hold?on,?fill([x(4-k),?xx,?x(3+k)],?[0,?yy,?0],?'g');?hold?off
???if?k<2
???????text(3.8,?0.6,?'[{\mu}-{\sigma},?{\mu}+{\sigma}]')
???else
???????kk?=?int2str(k);
???????text(3.8,?0.6,?['[{\mu}-',?kk,?'{\sigma},?{\mu}+',?kk,?'{\sigma}]'])
???end
???text(2.8,?0.3,?num2str(P(k)));?shg???%?填充區域內顯示面積
end
xlabel('x');?shg
繪圖結果為:
三、統計分析命令
- 分別計算矩陣各列的最大值或最小值,
- 若計算整個矩陣最大元素, 可用 或
- 分別計算矩陣各列的均值與中位值
- , 分別計算矩陣各列的樣本標準差與樣本方差
- 計算矩陣各列所組成列向量計算出的協方差矩陣, 注意到對應的分丹仍然是
- 計算矩陣x各列所組成列向量對應的相關系數
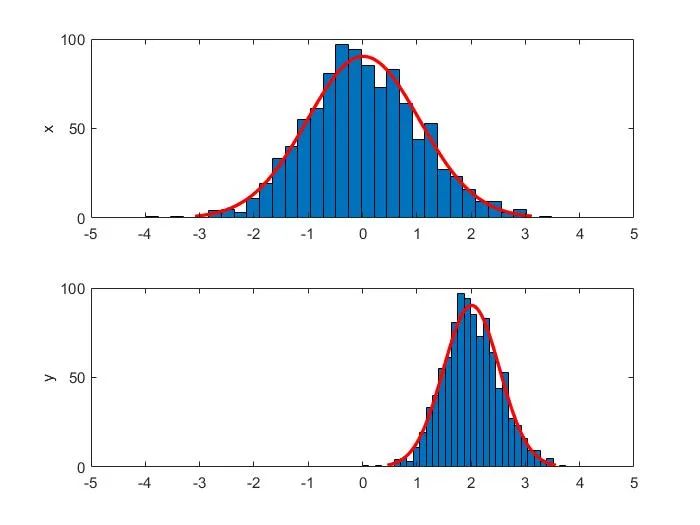
例:產生1000個服從的隨機數
mu?=?2;?s?=?0.5;
rng(22,?'v5normal')
x?=?randn(1000,?1);
y?=?s*x+mu;
subplot(2,?1,?1),?histfit(x),?axis([-5,?5,?0,?100]),?ylabel('x')
subplot(2,?1,?2),?histfit(y),?axis([-5,?5,?0,?100]),?ylabel('y')
四、多項式擬合
假設 我們獲取其函數曲線上的一組采樣點 利用數學方法確定或估計系數 的問題稱之為多項式擬合問題
一般來講,多項式擬合往往會與逼近或插值這兩種知識相結合。在采樣點準確,函數光滑的情況下,高階的擬合(即假設更大的 ) 往往效果更佳,但如果采樣信息有噪聲誤差, 過大的可能會讓結果失去擬合意義(一般設定 $n
p = ployfit(x, y, n)將通過數組和的數據進行擬合,擬合的階數或次數設定為自然數,返回多項式系數yy=polyval (p, x)可以將多項式系數回代,觀察擬合值
利用MATLAB函數計算采樣值向量與擬合值向量誤差的范數, 范數與范數,可以分析其平方殘差、絕對值殘差或一致逼近殘差的情況。
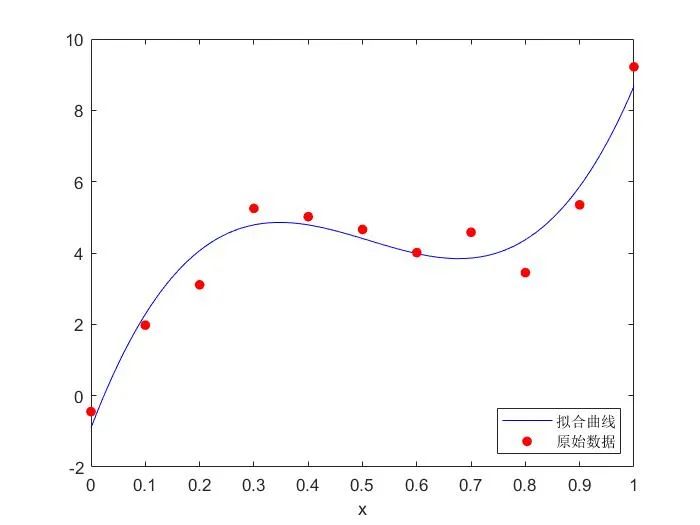
例:多項式擬合實例
x0?=?0:0.1:1;
y0?=?[-.447,?1.978,?3.11,?5.25,?5.02,?4.66,?4.01,?4.58,?3.45,?5.35,?9.22];?%?構造原始數據
n?=?3;P?=?polyfit(x0,?y0,?n)????????????%?多項式擬合
xx?=?0:0.01:1;?yy?=?polyval(P,?xx);????%?利用得到的多項式代回得到預測值
plot(xx,?yy,?'-b',?x0,?y0,?'.r',?'MarkerSize',?20);???????%?繪圖
legend('擬合曲線',?'原始數據',?'Location',?'SouthEast')
xlabel('x')
繪制結果為:
進階制表:
y1?=?polyval(P,?x0);
T?=?table(x0',?y0',?y1',?y1'-y0',?'VariableNames',?{'X',?'Y',?'Fit',?'FitError'})
表打印結果為:
T?=
??11×4?table
?????X???????Y?????????Fit???????FitError?
????___????______????________????_________
??????0????-0.447????-0.90431?????-0.45731
????0.1?????1.978??????2.2819???????0.3039
????0.2??????3.11??????4.0659??????0.95592
????0.3??????5.25??????4.7879?????-0.46211
????0.4??????5.02???????4.788?????-0.23204
????0.5??????4.66??????4.4063?????-0.25372
????0.6??????4.01???????3.983????-0.027002
????0.7??????4.58??????3.8583?????-0.72174
????0.8??????3.45??????4.3722??????0.92223
????0.9??????5.35???????5.865??????0.51503
??????1??????9.22??????8.6768?????-0.54316
1. 多項式擬合的最小二乘理解
polyfit函數的方法即解最小二乘問題 :
方法是構造
易得 在 時, 方程超定 (可能無解) , 此時最小二乘解可以通過 獲得
例:用最小二乘法獲得擬合結果
x0?=?(0:0.1:1)';
y0?=?[-.447,1.978,3.11,5.25,5.02,4.66,4.01,4.58,3.45,5.35,9.22]';
m?=?length(x0);
n?=?3;
X?=?zeros(m,n+1);?????????????????????%m個采樣點,n+1個未知系數
for?k=1:n
????X(:,?n-k+1)?=?(x0.^k);
end
X(:,?n+1)?=?ones(m,?1);
aT?=?(X\y0)'
輸出結果應與調用多項式擬合函數得到的P相同
aT?=
???56.6915??-87.1174???40.0070???-0.9043
2. 適用于特定問題的擬合或回歸方法
- 嶺回歸模型:本質上仍可化歸為最小二乘問題
其中, 表示擬合系數。
- Lasso模型:對擬合系數具有稀疏正則的模型:
- 最小絕對殘差 (LAR)模型:對離群值的處理有更好效果 :
實際問題中,線性擬合所使用的基函數也未必一定是多項式, 根據實際問題可以設置為三角函數、指數函數、正態分布的概率密度函數,以及混合定義的基底函數。











)







