【數據結構】圖的深度優先搜索

　　圖的深度優先搜索類似于樹的深度優先搜索。不同的是，圖中可能包括循環，即我們有可能重復訪問節點。為了避免訪問已經訪問過的節點，我們要使用一個布爾變量的數組。

　　例如，在下圖中，我們從節點2開始訪問。當訪問到節點0，我們尋找它的所有緊接節點。節點2也屬于節點0的鄰接節點。如果我們沒有標記訪問的節點，那么節點2 將會被重復訪問，這樣的話整個算法過程就不會停下來了。下圖的深度優先搜索是2，0，1，3

　　這種搜索算法所遵循的搜索策略是盡可能“深”地搜索一個圖。它的基本思想如下：首先訪問圖中某一起始頂點v，然后由v出發，訪問與v鄰接且未被訪問的任一頂點w1，再訪問與w1鄰接且未被訪問的任一頂點w2，......重復上述過程。當不能再繼續向下訪問時，一次退回到最近被訪問的頂點，若它還有鄰接頂點未被訪問過，則從該點開始繼續上述搜索過程，直到圖中所有頂點均被訪問過為止。

　　舉個例子：

　　

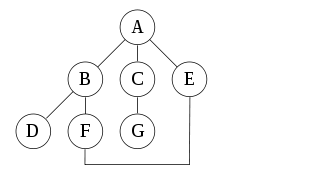
　　上圖一幅無向圖。我們從A點開始遍歷，并假設左邊的節點先被訪問到。那么訪問順序是A，搜索A所有可訪問的鄰接節點并選擇B，然后訪問B，搜索B所有可訪問的鄰接節點并選擇D，然后訪問D，搜索D的所有可訪問的鄰接節點。由于D只有一個鄰接節點B，而B已經被訪問過。所以回退到D的上級B（注意，不是訪問B，僅僅是回到上級）。然后再搜索B的所有可訪問的鄰接節點，AD已經被訪問過，所以訪問F。這個過程一直持續直到訪問過所有的節點。

　　選擇可訪問鄰接節點的時候，可以使用我們自己定義的順序。比如訪問A的鄰接節點的時候，可以先訪問B，也可以先訪問E。可根據需求靈活調整。

?

下述代碼是深度優先搜索的C++版本，有遞歸和迭代版本。圖的實現使用鄰接鏈表表示。STL的list被用來存儲鄰接節點。

#include<list>
#include<iostream>
using namespace std;class Graph {private:int V;list<int>* adj;void DfsUtil(int v, bool visited[]);public:Graph(int n);    //No of vertices~Graph();    //Pointer to an array containing adjacency listsvoid addEdge(int v, int w);    //function to add an edge to graphvoid Dfs(int s);    //Dfs traversal of the vertices reachable from vvoid DfsIter(int s);
};Graph::Graph(int v) {V = v;adj = new list<int>[V];
}Graph::~Graph() {delete []adj;adj = NULL;
}void Graph::addEdge(int v, int w) {adj[v].push_back(w);    //Add w to v's list
}void Graph::Dfs(int s) {bool* visited = new bool[V];for (int i = 0; i < V; i++)visited[V] = false;DfsUtil(s, visited);
}void Graph::DfsUtil(int v, bool visited[]) {//Mark the current node as the visited and print itvisited[v] = true;cout<<v<<" ";//Recur for all vertices adjacent to this vertexlist<int>::iterator i;for (i = adj[v].begin(); i != adj[v].end(); i++)if (!visited[*i])DfsUtil(*i, visited);
}void Graph::DfsIter(int v) {bool*  visited = new bool[V];for (int i = 0; i < V; i++)visited[i] = false;list<int> stack;stack.push_back(v);list<int>::iterator i;while (!stack.empty()) {v = stack.back();cout<<v<<" ";stack.pop_back();visited[v] = true;for(i = adj[v].begin(); i != adj[v].end(); i++)if (!visited[*i])stack.push_back(*i);} delete []visited;
}int main()
{// Create a graph given in the above diagramGraph g(4);g.addEdge(0, 1);g.addEdge(0, 2);g.addEdge(1, 2);g.addEdge(2, 0);g.addEdge(2, 3);g.addEdge(3, 3);cout << "Following is Depth First Traversal (starting from vertex 2) \n";g.DfsIter(2);return 0;
}

?

輸出：

Following is Depth First Traversal (starting from vertex 2)
2 0 1 3

?

參考資料：

　　1. http://www.geeksforgeeks.org/depth-first-traversal-for-a-graph/