
1、一元、多元函數導數與導數值計算
2、一元、多元函數高階導數的計算
3、抽象復合函數的一階、高階導數計算
4、全微分的計算
5、方向導數的計算
工具:WolframAlpha計算搜索引擎
位置:http://www.wolframalpha.com,打開網頁直接操作,其中windows app也可以通過Windows 10應用商店下載安裝!
特別提示:如果使用網頁版執行操作,不需要下載、安裝任何軟件,也不需要點任何鏈接,直接網頁打開的那個搜索文本編輯框(如下圖)輸入表達式就可以了!系列推文中除特別強調外,顯示的結果都能直接看到的!

手機:可以直接打開網頁操作,或者自行網絡搜索下載安裝WolframAlpha APP版本操作
執行界面:網頁、手機或平板等操作界面基本一致.
1、一元、多元函數一階導數與導數值的計算
例1 ?計算以下函數的導數,并求在處的導數值:
輸入表達式為
d/dx((x^3)cos(5x^2+e^(2x))-ln(3x^3-2x))執行后的結果如下圖所示.
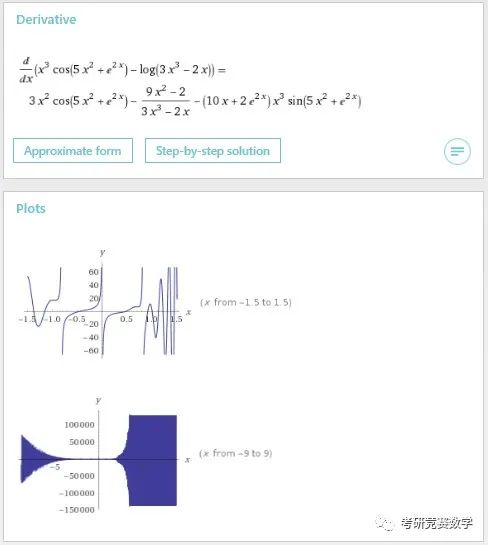
結果不僅顯示導數結果,也給出了函數在不同范圍內的圖形. 輸入表達式也可以直接以更自然的語言描述形式輸入,比如輸入:
derivative of (x^3)cos(5x^2+e^(2x))-ln(3x^3-2x)執行計算得到的結果一致.
在以上兩種輸入的表達式后面加上where x=1,比如輸入
derivative of (x^3)cos(5x^2+e^(2x))-ln(3x^3-2x) where x=1執行計算后即得到導數值為
例2 ?計算以下函數的一階偏導數和在處的偏導數值:
關于的偏導數計算輸入表達式為
d/dx(a sin(x^3+y^2)-(x+y^(1/2))^(1/2))執行后的結果為
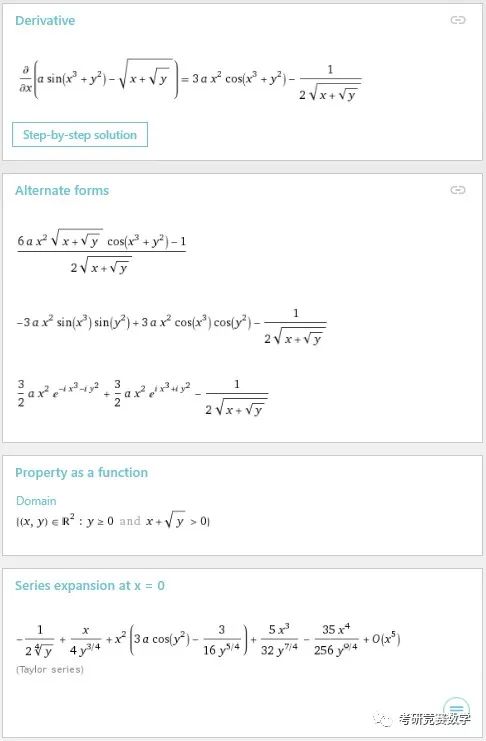
結果除了最上面給出導數結果之外,在下面還以不同的形式給出了導數結果描述. 另外給出了二元函數的定義域與關于變量的帶皮亞諾余項的麥克勞林公式.
在以上表達式后面加上where (x,y)=(1,1),即可得該點處的偏導數值. 即輸入
d/dx(a sin(x^3+y^2)-(x+y^(1/2))^(1/2)) where (x,y)=(1,1)執行計算后得到導數值為.
關于的偏導數計算輸入表達式只要將以上輸入表達式中的求導變量改為y就可以了. 即
d/dy(a sin(x^3+y^2)-(x+y^(1/2))^(1/2))執行后的結果除了導數結果不同外,其余顯示內容基本一致. 其中在處的一階導數值為.
【注】 ?以上求導變量也可以指定為求導變量,比如輸入
d/da(a sin(x^3+y^2)-(x+y^(1/2))^(1/2))則計算結果為,即對變量求導,并顯示導數結果圖形.
2、一元、多元函數高階導數的計算
例1 ?計算以下函數的50階導數:
輸入表達式為
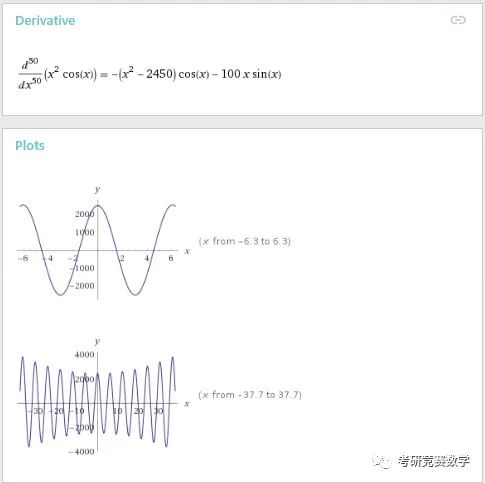
d^50/dx^50((x^2)cosx)執行后的結果顯示為
例2 ?求以下函數關于的三階偏導數與關于的二階偏導數的混合高階偏導數:
輸入表達式為
d^3/dx^3 d^2/dy^2 ((x^2+y^2)e^(x+y))執行后顯示結果.? 結果除了顯示偏導數外,還會顯示結果曲面圖、等值線圖,可能的其他表達形式以及方程的根分布情況,級數展開形式,不定積分及誒過與極小值點與極小值等信息,如下圖.

3、抽象復合函數的一階、高階導數計算
將上面具體函數求導的函數表達式換成抽象函數即可.
例1 ?計算下列函數的一階、二階導數:
輸入表達式為
d/dx (x^2)f(3x+4cosx), d^2/dx^2 (x^2)f(3x+4cosx)執行后的結果為

由于除了外還包含其他符號,所以結果以偏導數描述形式其輸入形式.
例2 ?計算以下函數的導數:
輸入表達式為
d^2/dx^2 f(x y, x^2-y^2), d/dx d/dy f(x y, x^2-y^2)執行后的結果為

4、全微分的計算
由于一元函數的微分就是導數乘以自變量微分
即完全可以直接歸結為導數的計算,下面僅僅介紹多元函數全微分的計算方法.
例 ?計算以下函數的全微分:
直接輸入表達式為
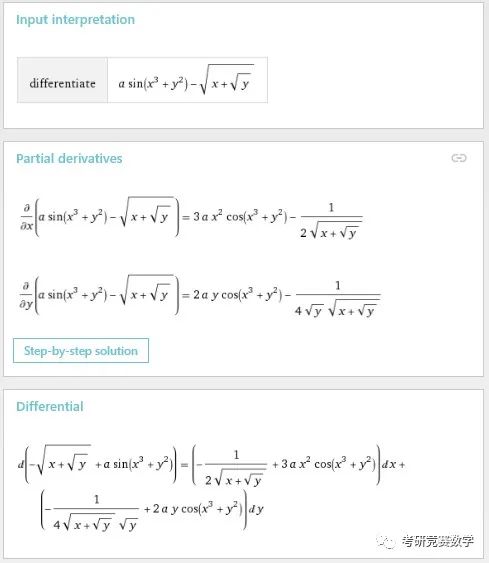
derivative of a sin(x^3+y^2)-(x+y^(1/2))^(1/2)自動識別變量為, ,執行計算后的結果不僅會得到全微分表達式,也會單獨列出兩個偏導數. 顯示結果如下:
其中derivative可以替換為differential. 也可以直接基于Wolfram語言,也即Mathematica中的命令來執行計算,比如輸入表達式
Dt(a sin(x^3+y^2)-(x+y^(1/2))^(1/2))則將表達式中的符號都識別為變量符號,執行計算得到全微分表達式. 如下圖.

只要令結果表達式中不是變量的符號,比如這里a它的微分令為0,即,得到的結果就是關于所有變量的微分表達式.
5、方向導數的計算
例1 ?計算以下函數指定方向的方向導數:
輸入表達式為
derivative of x e^(2y)+cos(x y) in the direction (3,-4)執行后的結果顯示為
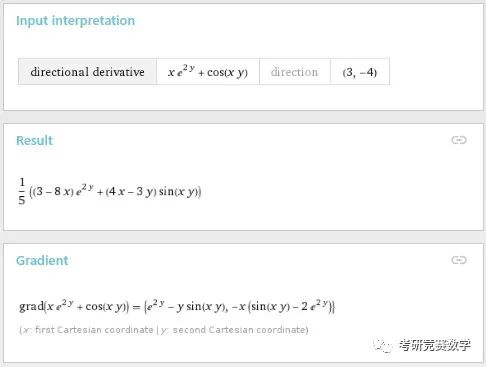
不僅給出了方向導數,也給出了函數的梯度向量.
例2 ?計算以下函數指定方向的方向導數:
輸入表達式為
derivative of f(x,y) in the direction (a,b)執行后的結果顯示為
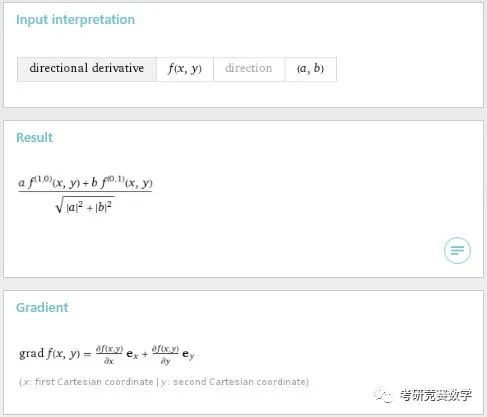
例3 ?計算以下函數指定方向和點處的方向導數:
輸入表達式為
derivative 3x^2+2y^2+z^2 in direction (-2,-2,1) at point (1,2,3)執行后的結果顯示為
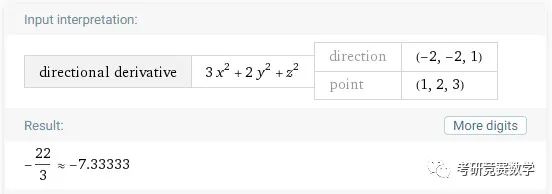
當然以上計算也可以直接依據求偏導數與方向導數計算公式,逐步計算代入得到結果.
微信公眾號:考研競賽數學(ID: xwmath)大學數學公共基礎課程分享交流平臺!支持咱號請點贊分享!

↓↓↓點查看更多相關內容


 JavaEE架構)

)














