理論物理極礎9：相空間流體和吉布斯-劉維爾定理

萊尼喜歡看河，尤其喜歡看漂浮物順流而下。他猜想漂浮物如何穿過礁石，如何陷入漩渦。但是河流整體，水量，流切變，河的分流和匯聚，這是萊尼所看不到的。

相空間流體

在經典力學里，注視一個特別的初始條件，再隨之在相空間走過特定軌跡，這是很自然的事情。但是還有一個更大的圖像，突出強調軌跡的總集合。這個更大的圖像可以直觀顯示所有可能的起點和所有可能的路徑。不要再拿著鉛筆點住相空間一點，然后沿著一條路徑畫線，而是做點更有雄心的事情。想象一下，你有無窮多支鉛筆，用它們在相空間均勻地點點（均勻在這里的意思是在\(q,p\)空間點的密度處處相等）。把這些點看做假想的填充相空間的流體的組成粒子。

每個點都按照哈密頓方程運動：

\begin{equation} \begin{split} & \dot{q}_i=\frac{\partial H}{\partial p_i}\\ & \dot{p}_i=-\frac{\partial H}{\partial q_i} \end{split} \label{eq1} \end{equation}

這樣，流體連綿不斷地流過相空間。

諧振子是說明相空間流體的好例子。在第8講，我們看到每個點做勻速圓周運動。（注意：我們談的是相空間，不是坐標空間，在坐標空間，諧振子做的是一維往復運動。）整個流體做剛性運動，繞著相空間原點做勻速圓周運動。

現在我們回到一般情況。如果坐標數目是\(N\)，則相空間就是\(2N\)維的。相空間流體以特定的方式流動。流動的特點之一是，每一點的能量值——\(H(q,p)\)的值——始終保持不變。能量相等的點組成一個平面，比如能量值為\(E\)的平面由以下方程描述：

\begin{equation}
H(q,p)=E
\label{eq2}
\end{equation}

對于每個\(E\)，都有一個關于\(2N\)個相空間變量的方程，因此可以定義一個\(2N-1\)維的面。換言之，每個\(E\)都對應一個面，所有的\(E\)對應的面可填充整個相空間。你可把相空間看做按方程\eqref{eq2}定義的等能線圖，如圖1。如果相空間流體的一點位于某等能面上，這點就會一直呆在這個等能面上。這就是能量守恒。

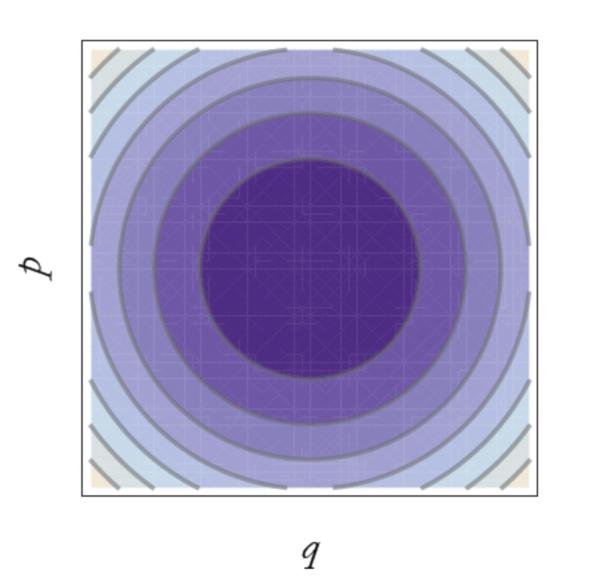
圖1 諧振子等能面

對于諧振子，相空間是二維的，能量面是圓，圓的方程為：

\begin{equation} \frac{\omega}{2}(q^2+p^2)=E \label{eq3} \end{equation}

對于一般的力學系統，能量面非常復雜，無法畫出來，但是原理是一樣的：能量面一層一層填充相空間，相空間流體流動過程中保持各點一直呆在初始時刻所在的能量面內。

簡短回顧

我們暫停一下，回顧一下第1講的內容。在第1講，我們討論過硬幣、色子，還有運動定律最基本的思想。我們描述這些定律用的方法，是用箭頭連著表示系統狀態的點，表示系統演化的過程和方向。我們還解釋過，有些定律是允許的，有些定律是禁止的，可允許的定律是可逆的。可允許的定律有什么特點？答案是每個點都有一個箭頭指向自己，也有一個箭頭從自己指向別的點。如果有一點，指向自己的箭頭多于從自己指向外部的箭頭，則相應的定律是不可逆的。同樣地，從自己指向外部的箭頭多于指向自己的箭頭，相應的定律也是不可逆的。這兩種情況都是禁止的。現在我們分析一下相空間流體流動的可逆性。

流和散度

我們考慮通常空間里流體流動的幾個簡單的例子。暫時先忘掉相空間，只考慮通常的三維空間（坐標軸分別為\(x,y,z\)）的普通流體。流動可用速度場描述。空間每一點的速度矢量都標記出來，所有這些速度矢量就組成速度場\(\vec{v}(x,yz)\)，如圖2所示。

圖2. 速度場

我們還可以用速度的分量描述速度場：\(v_x(x,y,z),v_y(x,y,z),v_z(x,y,z)\)。一點的速度也可能是依賴時間的，但是我們只考慮不依賴時間的情況，即只考慮定常流。

我們還假設流體是不可壓縮的，即一定量的流體總占據同樣的體積，也即流體密度（單位體積內的分子數）是均勻的并且是保持不變的。考慮如下小立方體盒子：

\begin{equation*} \begin{split} & x_0\leq x\leq x_0+dx \\ & y_0\leq y\leq y_0+dy \\ & z_0\leq z\leq z_0+dz \end{split} \end{equation*}

不可壓縮性意味著每個這么大盒子里的流體粒子數都是一定的，并且單位時間凈流入盒子的流體也是0（流入流出的流體正好相等）。單位時間從面\(x=x_0\)流入盒子的分子數目，正比于穿過此面的流速 \(v_x(x_0)\)。

如果\(v_x(x_0)=v_x(x_0+dx)\)，則從\(x=x_0\)處流入盒子的流體等于從\(x=x_0+dx\)處流出盒子的流體。但是，如果\(v_x\)隨位置變化，流入流出的流體就不相等，從這兩個面凈流入盒子的流體分子數正比于

\begin{equation*} -\frac{\partial v_x}{\partial x}dxdydz \end{equation*}

同樣的道理也適用于\(y_0\)和\(y_0+dy\)，也適用于\(z_0\)和\(z_0+dz\)。把這三項都加起來，即凈流入盒子的分子數為

\begin{equation*} -\left (\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}\right )dxdydz \end{equation*}

括號里面的各導數有一個專門的名字：矢量場\(\vec{v}(t)\)的散度，記為：

\begin{equation} \nabla \cdot \vec{v}=\left (\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}\right ) \label{eq4} \end{equation}

散度之名恰如其分，表示流體的分子外散而流，增大流體占據的體積。如果流體是不可壓縮的，流體的體積不變，因此散度必須為0。

理解不可壓縮性的一個方法是，認為流體的各分子，或是流體中的各點，都是不可壓縮的，不能壓縮進更小的體積，也不可以憑空消失或出現。發揮點想象力，你可以看出不卡壓縮性與可逆性非常類似。在第1講的各例子中，箭頭也定義一種流。在某種意義上說，至少在可逆情況下，這種流也是不可壓縮的。現在可以提出一個問題，相空間中的流動是不可壓縮的嗎？答案是，是的，如果系統滿足哈密頓方程的話。有一個定理表述了這種不可壓縮性，這個定理就是劉維爾定理。

劉維爾定理

我們再回到相空間中的流動，考慮相空間中每點流速的分量。相空間流體不是三維的，而是\(2N\)維的，坐標為\(q_i\)、\(p_i\)。因此速度場有\(2N\)個分量，\(N\)個\(q_i\)，\(N\)個\(p_i\)，分量記為\(v_{q_i}\)和\(v_{p_i}\)。

方程\eqref{eq4}所定義散度概念，很容易推廣至任意維空間，相空間流體的散度為以下\(2N\)項的和：

\begin{equation} \nabla \cdot \vec{v}=\sum_i \left (\frac{\partial v_{q_i}}{\partial q_i}+\frac{\partial v_{p_i}}{\partial p_i}\right ) \label{eq5} \end{equation}

如果流體是不可壓縮的，那么方程\eqref{eq5}比為0。要證明這一點，我們需要知道速度場的分量，即假想的相空間流體的組成粒子的速度。

相空間中任意一點的速度的分量為：

\begin{equation*} \begin{split} & v_{q_i}=\dot{q}_i\\ & v_{p_i}=\dot{p}_i \end{split} \end{equation*}

而且，\(\dot{q}\_i\) 和 \(\dot{p}\_i\)正是哈密頓方程中的量，根據方程\eqref{eq1}，有

\begin{equation} \begin{split} & v_{q_i}=\frac{\partial H}{\partial p_i}\\ & v_{p_i}=-\frac{\partial H}{\partial q_i} \end{split} \label{eq6} \end{equation}

把方程\eqref{eq6}帶入方程\eqref{eq5}，得

\begin{equation} \nabla \cdot \vec{v}=\sum_i \left (\frac{\partial }{\partial q_i}\frac{\partial H}{\partial p_i}-\frac{\partial }{\partial p_i}\frac{\partial H}{\partial q_i}\right ) \label{eq7} \end{equation}

二階導數，如\(\frac{\partial }{\partial p_i}\frac{\partial H}{\partial q_i}\)，結果與求導順序無關，因此方程\eqref{eq7}中括號中的兩項正好抵消，因此有：

\begin{equation*} \nabla \cdot \vec{v}=0 \end{equation*}

因此，相空間中流體是不可壓縮的，這在經典力學中被稱為劉維爾定理，盡管與法國數學家約瑟夫·劉維爾幾乎沒什么關系。這個定理是美國物理學家吉布斯于1903年首先發表的，因此也稱為吉布斯-劉維爾定理。

我們前面提到，流體不可壓縮意味著每個小盒子的凈流入量為0，這也是流體的不可壓縮性的定義。這個定義還有個等價的表述。想象某個時刻一定體積的流體，這團流體可以為任何形狀。追蹤流體中每一點的運動，過一段時間后，這團流體就會呈現出其他形狀，但是只要流體是不可壓縮的，這團流體的體積就保持不變，在任意時刻的體積都與初始時刻的體積相同。因此劉維爾定理可重新表述為：任意一團相空間流體的體積都不隨時間變化。

比如諧振子，相空間流體繞著原點做圓周運動，很明顯任意一團相空間流體的體積保持不變，甚至它們連形狀也不變。但是形狀不變是諧振子的特殊性質。現在我們看另一個例子。考慮如下形式的哈密頓量：

\begin{equation*} H=pq \end{equation*}

你很可能沒見過這個哈密頓量，但是這個哈密頓量完全可以存在的。我們先寫出運動方程：

\begin{equation*} \begin{split} & \dot{q}=q\\ & \dot{p}=-p \end{split} \end{equation*}

解出這個微分方程組，可以看出\(q\)隨時間指數增大，\(p\)以同樣的速率隨時間指數減小。換言之，流沿著\(p\)軸壓縮，而沿著\(q\)軸膨脹，壓縮的量與膨脹的量相同。每一團流體沿著\(q\)軸被拉伸，沿著\(p\)軸被擠壓。很明顯，流體團形狀極端扭曲，但是相空間體積不變。

劉維爾定理是與第1講中的可逆性最接近的類比。在量子力學里，劉維爾定理被代之以幺正性。

泊松括號

19世紀法國數學家思考力學的時候發明了這些極其漂亮的數學形式，他們在想些什么呢？（哈密頓例外，他是愛爾蘭人）他們是如何得到作用量原理、拉格朗日方程、哈密頓量、劉維爾定理？他們是在解物理題嗎？他們只是為了玩出漂亮的方程嗎？還是只是為了設計新的物理原理？我認為這些因素都有一點，但在各個方面都取得了極大成功。但是這些極大的成功直到20世紀量子力學被發現之后才變得清晰。看起來好像數代人之前的數學家機具洞察力，他們發明了百年之后量子概念的等價概念。

還沒完。還有一個力學形式理論，即泊松括號，以法國數學家泊松的名字命名，這好像也是個超越時代的理論。下面我們介紹泊松括號。考慮某個關于\(q_i\)和\(p_i\)的函數，這樣的函數有動能、勢能、角動量等等，當然還有其他各種我們可能感興趣的物理量。我們先不指明具體函數，記為\(F(q,p)\)。

我們現在細致考察\(F(q,p)\)。首先，它是相空間中的位置的函數。但是如果我們追蹤相空間中任何一點——體系的任何真實的軌跡——都對應一個函數值\(F\)，即\(F\)的值隨沿著軌跡而變。換言之，體系沿著某軌跡的運動使\(F\)稱為時間的函數。我們現在計算\(F\)如何隨著給定一點的運動而變，即計算\(F\)的時間導數：

\begin{equation*} \dot{F}=\sum_i \left ( \frac{\partial F}{\partial q_i}\dot{q}_i+\frac{\partial F}{\partial p_i}\dot{p}_i \right ) \end{equation*}

代入哈密頓方程，得：

\begin{equation} \dot{F}=\sum_i \left ( \frac{\partial F}{\partial q_i}\frac{\partial H}{\partial p_i}-\frac{\partial F}{\partial p_i}\frac{\partial H}{\partial q_i} \right ) \label{eq8} \end{equation}

我也不知道泊松如何發明了他的括號，我懷疑是方程\eqref{eq8}的右邊他寫煩了，決定用新的符號簡化一下。拿出兩個相空間的函數，\(G(q,p)\)和\(F(q,p)\)。先不管它們的物理意義，也不管是不是其中一個是否是哈密頓量。\(F\)和\(G\)的泊松括號定義為：

\begin{equation} \{F,G\}=\sum_i \left ( \frac{\partial F}{\partial q_i}\frac{\partial G}{\partial p_i}-\frac{\partial F}{\partial p_i}\frac{\partial G}{\partial q_i} \right ) \label{eq9} \end{equation}

泊松再寫方程\eqref{eq8}就簡潔了，可寫為：

\begin{equation} \dot{F}=\{F,H\} \label{eq10} \end{equation}

方程\eqref{eq10}神奇之處在于它的涵意極其豐富。任何物理量的時間導數都可以寫為該物理量與哈密頓量的泊松括號。甚至連哈密頓方程本身也包括在內。要看出這一點，令\(F\)為任何一個\(q\)，由方程\eqref{eq10}，有：

\begin{equation*} \dot{q}_k=\{q_k,H\} \end{equation*}

把上式中的泊松括號寫開，其實只有一項，即\(q_k\)對自身的求導那一項。由于\(\frac{dq_k}{dq_k}=1\)，于是泊松括號\(\{q_k,H\}\)恰好等于\(\frac{\partial H}{\partial p_k}\)，這正是哈密頓方程組中的第一個方程。同理，哈密頓方程組的第二個方程等價于

\begin{equation*} \dot{p}_k=\{p_k,H\} \end{equation*}

注意到在這個形式理論中，哈密頓方程組的泊松括號形式的這兩個方程是同號的，\(q\)和\(p\)分別對應的方程的符號差異隱藏在泊松括號的定義里。

法國人對優雅的迷戀回報豐厚。泊松括號成為量子力學里最基本的量：對易子。