-----------最小生成樹----------------

最小生成樹(Minimum Spanning Tree)

　　1:是一棵樹(是一種特殊的圖)

　　　　　　連通的,沒有回路 有V 個頂點 一定有 V-1條邊

? ? ?2:生成樹

　　　　　　包含了全部的頂點,所有的V-1條邊 ?都在圖里

剩下的三個土 ?都是第一個完全圖的生成樹

只要是 4個頂點 3條邊 ? 沒有回路 就是生成樹 ? ? 這3個圖 隨便的加一條邊 ?都會變成一個回路 ? 也就不是 最小生成樹了. ??

　　3:最小??

　　　　　　　　邊的權重之和最小

最小生成樹存在 ?和 ? 圖連同 ?是充分必要條件

?---------------------------------------------------------------------------------------------------------------------------

不論什么方法解決最小生成樹問題都離不開 貪心算法

什么是貪 : 每一步都要最好的 .

什么是好 : 權重最小的邊 .?

需要約束: ? ? ? ? ? ? ? ? ? ? ? ??

只能用圖里面的邊.

只能剛好用掉V-1條邊

不能有回路

貪心算法之一

Prim算法-讓一顆小樹長大

?用Dijkstra算法和Prim算法比較一下感覺幾乎一樣

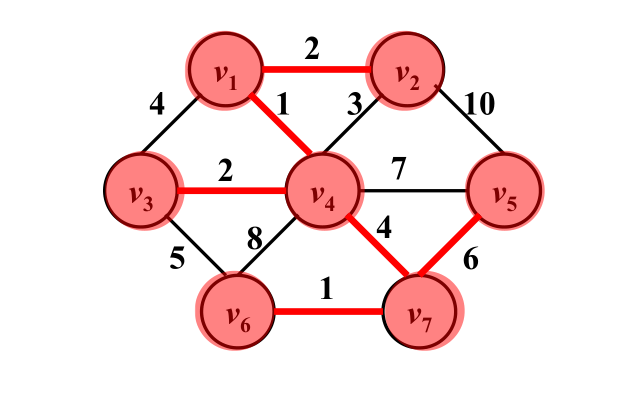
Prime算法 ?生成樹的順序是V1,V4,V2,V3,V7,V6,V5,

//                       Dijkstra算法
/*依鄙人之見,Dijkstra算法 就是走一個一定最小的步子,走完之后丈量一下去下一個地方需要多少步然后 給那個地方打上標簽
這時候     可能會出現  A->B  為80    但是 A->C->B  為   5的情況   所以 在走完第一步之后  在第一部的基礎上丈量完 然后走  離現在距離最近的點這個點 該點一定沒有 A 離源點近  但是改點是距離 A最近的     就這樣 逐步求最小  不停的修改
*/
void Dijkstra( Vertex s )  //  看來  再看一遍  寫筆記  很重要
{ while (1) {V =  未收錄頂點中dist 最小者;if (  這樣的V在 不存在 )break;collected[V] = true;for ( V 點 的每個鄰接點 W )if ( collected[W] == false )if ( dist[V]+E <V,W> < dist[W] ){dist[W] = dist[V] + E <V,W> ;path[W] = V;}}
}

?

//                    Prim算法

void Prim()
{MST=(s);while(1){V=未收錄頂點中dist最小者  // 和源點相鄰的就是權重 . 剩下的是正無窮.if(都被收錄了)break;dist[V]=0;//將V收錄進MST      for(V的 每個臨接點W){if(dist[W]!=0)  //沒有被收錄 的話
            {if(E(v,w)<dist[W]){dist[W]=E(v,w);parent[W]=V;}}}}if(MST中的頂點不到V個)   //就是  有獨立的點   不連通的圖.
        ERRor(生成樹不存在)
}

?

----------------圖比較稀疏----------------?

//                    Kruskal算法
//這個算法的核心就是    貪心了      將每一條邊 一個一個的收錄進去 (不能有回路)(變得個數是點的個數-1)void
void Kruskal(Graph G)
{MST={};   //生成一個空樹while(MST中不到V-1條邊&&E中還有邊){從E中取一條權重最小的邊E(v,w);  //用最小堆
        將E(v,w)從E中刪除;if(E(v,w)不再MST中構成回路)   //  用并查集
            將E(v,w)加入MTS;else徹底無視E(v,w);}if(MST中不到V-1條邊)Error("生成樹不存在");
}

?