R--線性回歸診斷（一）

線性回歸診斷--R

?【轉載時請注明來源】：http://www.cnblogs.com/runner-ljt/

??? Ljt ? 勿忘初心 ?無畏未來

? ? 作為一個初學者，水平有限，歡迎交流指正。

?

---

?

? 在R中線性回歸，一般使用lm函數就可以得到線性回歸模型，但是得到的模型到底合不合適？在我們使用所得到的線性模型之前就需要進行回歸診斷。

? ??線性回歸的診斷，主要是檢驗線性回歸模型的假設是否成立。

? ? 線性回歸模型 ? ?y=Θ₀+Θ₁x₁+Θ₂x₂+.......+Θ_mx_m+ε ? ?（自變量與因變量之間是線性關系）

? ? 基本假設：

（1）隨機干擾項?ε 服從零均值，同方差，零協方差（相互獨立）的正態分布

? ? ? ? ? ?E(ε_i)=0 ?; ??var(ε_i)=σ^{2 ??}; ^??cov(ε_i ,?εj)=0 ? ? ;

? ? ? ? ? ?ε_i~N(0,σ²)

（2）隨機干擾項?ε 與解釋變量間不相關

? ? ? ? ? ?cov(X_i , ε_i) =0

?

---

?

（一）顯著性檢驗

? （1）回歸方程顯著性 F 檢驗 ：?看自變量 X₁?, X₂?.....X_m ?從整體上對隨機變量Y是否有明顯的影響 。

? ? ? ? ? 原假設 H₀：Θ₁ =Θ₂=.....=Θ_m=0 ? ? ? ?（H_0?若被接受則表明隨機變量Y與X₁?, X₂?.....X_m?之間的關系由線性回歸模型表示不合適）

? ? ? ? ? P值<α ?: ?拒絕原假設 。即在顯著性水平?α 下，Y 與?X₁?, X₂?.....X_m 有顯著的線性關系，回歸方程是顯著的。（自變量全體對因變量產生線性影響）

?

? （2）回歸系數顯著性 t 檢驗：看單個的自變量?X_i 對Y是否有明顯影響。

? ? ? ? ? 原假設 ? H_0i?：Θ_i?=0 ? ? ? ? ? ?（H_0i?若被接受則表明自變量X_i 對因變量Y的線性效果不顯著）

? ? ? ? ??P值<α ?: ? 拒絕原假設 。即在顯著性水平?α 下，Y 與?X_i?有顯著的線性關系。

?

? ? ? ? ?對于一元線性回歸這兩種檢驗是等價的；

? ? ? ? ?對于多元線性回歸，這兩種檢驗是不等價的:

? ? ? ? ?F檢驗顯著，說明Y對自變量X₁?, X₂?.....X_m 整體的線性回歸效果是顯著的，但不等于Y對每個自變量X_i 的效果都顯著;反之，某個或某幾個X_i 的系數不顯著，回歸方程顯著性的F檢驗仍然有可能是顯著的。由于某些自變量不顯著，因而在多元回歸中并不是包含在回歸方程中的自變量越多越好，需要剔除對Y無顯著影響的自變量。

?

（二）擬合優度

? ? ? ? 擬合優度用于檢驗回歸方程對樣本觀測值的擬合程度。

? ? ? ? 樣本決定系數 R^2?= SSR/SST = 1 - SSE/SST ? ? ?（R²屬于[0,1]?）

? ? ? ? ? ? ? R² 越接近 1 ，表明回歸擬合的效果越好；

? ? ? ? ? ? ? R^2?越接近 0 ，表明回歸擬合的效果越差。

? ? ? ? 與F檢驗相比，R² 可以更清楚直觀地反映回歸擬合的效果，但是并不能作為嚴格的顯著性檢驗。需要指出的是，擬合優度并不是檢驗模型優劣的唯一標準，有時為了使模型從結構上有較合理的經濟解釋，在樣本量n 較大時，R² 等于0.7左右我們也給回歸模型以肯定態度。需要注意的是?R²與回歸方程匯中自變量的數目以及樣本量n有關，當樣本量n與自變量的個數接近時，R²易接近于1，其中隱含著一些虛假的成分。

?

---

?

下面結合實例對R語言中線性擬合函數lm的結果進行分析

?

?

> 
> 
> head(bank)y     x1     x2    x3     x4
1 1018.4  96259 2239.1 50760 1132.3
2 1258.9  97542 2619.4 39370 1146.4
3 1359.4  98705 2976.1 44530 1159.9
4 1545.6 100072 3309.1 39790 1175.8
5 1761.6 101654 3637.9 33130 1212.3
6 1960.8 103008 4020.5 34710 1367.0
> 
> fline<-lm(y~x1+x2+x3+x4,data=bank)
> summary(fline)Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = bank)Residuals:Min      1Q  Median      3Q     Max 
-487.35  -78.89   -2.65  137.02  403.78 Coefficients:Estimate Std. Error t value Pr(>|t|)    
(Intercept) -4.168e+03  1.193e+03  -3.495 0.002998 ** 
x1           5.842e-02  1.216e-02   4.805 0.000194 ***
x2           4.142e-01  3.218e-02  12.871 7.41e-10 ***
x3          -1.384e-02  8.520e-03  -1.624 0.123826    
x4          -7.062e-01  1.750e-01  -4.035 0.000959 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 217.7 on 16 degrees of freedom
Multiple R-squared:  0.9982,	Adjusted R-squared:  0.9978 
F-statistic:  2222 on 4 and 16 DF,  p-value: < 2.2e-16> 
> 

?

　　

回歸結果的診斷：

?（1）F-statistic

? ? ? ? ?回歸方程顯著性 F 檢驗中的F統計量，其P值<2.2e-16<0.05 ，表明Y 與?X₁?, X₂?,X₃,X₄有顯著的線性關系，回歸方程整體是顯著的。

?（2）Coefficients

? ? ? ? ?Estimate 即回歸系數的估計值，其對應的 P(>|t|)為各回歸系數t檢驗的P值。

? ? ? ? ?從回歸結果看，X3的P值為0.123826>0.05,表明X3對Y沒有顯著影響，應考慮刪除變量X3；其他三個變量的P值都<0.05,對Y 都有顯著的影響。

?

? ?---------以上兩個回歸檢驗的結果也表明，自變量整體對于因變量有顯著影響，并不表明每個自變量對因變量都有顯著影響。

?

?（3）Multiple R-squared ?; ? Adjusted R-squared

? ? ? ? ?分別表示 ‘擬合優度’ ?，‘修正的擬合優度’

? ? ? ? ?擬合優度值為 0.9982 ?很接近于 1 ，表明回歸方程對樣本觀測值的擬合程度較高。

?

---

?

?

相關圖形診斷：

? （1）殘差圖?

? ? ? ? ? 殘差圖分析法是一種直觀、方便的分析方法。它以殘差e_i?為縱坐標，以其他適宜的變量（如樣本擬合值）為橫坐標畫散點圖,主要用來檢驗是否存在異方差。

? ? ? ? ? 一般情況下，當回歸模型滿足所有假定時，殘差圖上的n個點的散布應該是隨機的，無任何規律。如果殘差圖上的點的散布呈現出一定趨勢（隨橫坐標的增大而增大或減小），則可以判斷回歸模型存在異方差。

? ? ? ? ? ?異方差：某一因素或某些因素隨著解釋變量觀測值的變化而對被解釋變量產生不同的影響，導致隨機誤差產生不同方差。

? ? ? ? ? ? ? ? ? ? ? ?當存在異方差時，普通最小二乘估計存在以下問題：

? ? ? ? ? ? ? ? ? ? ? ?（i） ?參數估計值雖然是無偏的，但不是最小方差線性無偏估計；

? ? ? ? ? ? ? ? ? ? ? ?（ii） 參數的顯著性檢驗失效；

? ? ? ? ? ? ? ? ? ? ? ?（iii） 回歸方程的應用效果極不理想。

?

? （2）Q-Q圖

? ? ? ? ? Q-Q圖主要用來檢驗樣本是否近似服從正態分布。

? ? ? ? ? 對于標準狀態分布而言，Q-Q圖上的點近似在Y=X直線附近。

?

? （3）標準化殘差方根散點圖

? ? ? ? ? 此圖類似于殘差圖，只是其縱坐標變為了標準化殘差的絕對值開方。

? ? ? ?

? （4）Cook距離圖

? ? ? ? ? 庫克距離用來判斷強影響點是否為Y的異常值點。

? ? ? ? ? 一般認為 ?當D<0.5時認為不是異常值點；當D>0.5時認為是異常值點。

? ??

> 
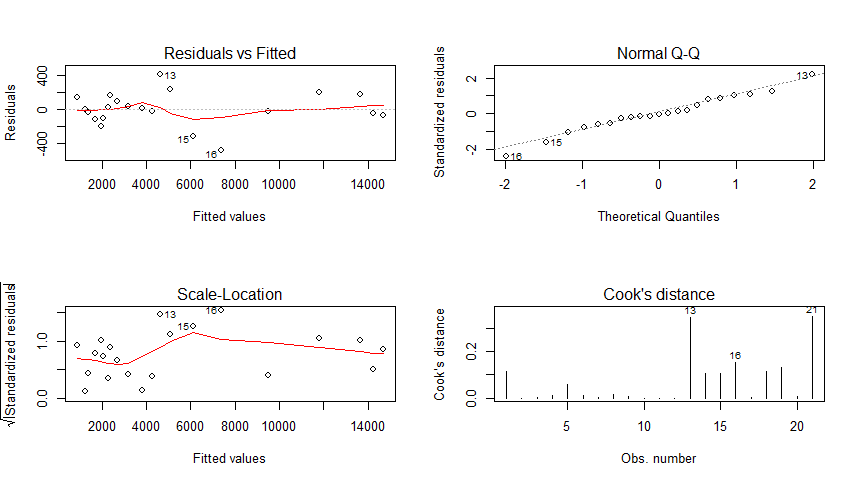
> par(mfrow=c(2,2))
> plot(fline,which=c(1:4))
> 

?

? ? ? ? ? ? ? ? ? ? ? ? ? ??

?

? ?從回歸的四個圖形結果來看：

? ? ? ? ? 殘差圖 ? Residuals vs Fitted ?: ?圖上的點基本服從隨機分布，可以認為不存在異方差的情況；

? ? ? ? ? 標準Q-Q圖 ?Normal Q-Q ? ? ? : ?圖上的點基本都在y=x直線附件，可認為樣本近似服從正態分布；

? ? ? ? ? 標準化殘差方根散點圖 Scale-Location：類似與殘差圖，點的分布基本是隨機的。

? ? ? ? ? 庫克距離圖 Cook‘s distance ? : ?最大的庫克距離為0.3左右，可以認為沒有異常值點。

? ? ? ? ? ? ??

? ?

? ??

?

?

?

?

?

?

?

?

?

?

?

?

?

?

---

?