1.概念

：大O符號是用來表達一個算法的復雜程度的，是一個數量級

2.代碼

a = 1
b = 2
c = 3
for i in range(n):for j in range(n):x = i*iy = j*jz = i*jfor k in range(n):m = a*k + 5v = k*kd = 100*c
e = c*d

3.分析

在上述代碼中，分配操作數分為四個操作數的總和。第一項是3，即前面三個賦值語句；第二項是3n^2,兩個嵌套循環，并且內層循環中有三個式子；第三項是2n,一個循環；第四個是2，兩個賦值語句。
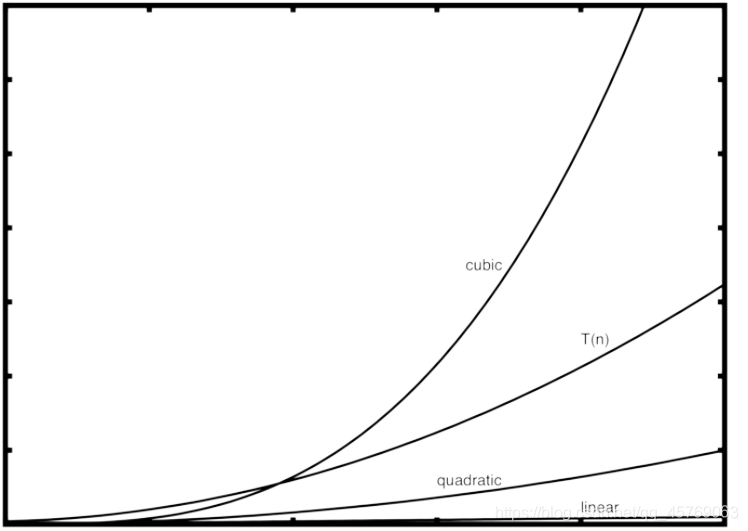
因此分配操作數T（n）=3+3n^2 + 2n + 2 = 3n^ 2+2n+5，當n變化到非常大時，其他項可以忽略不計，即O(n)=n^2

4.其它

1）python排序函數是需要成本的，即一般排序sort函數的復雜度是O(n^2)或者O(nlogn)

2)復雜度的計算，一般是根據是否有嵌套和每一個循環的步長以及循環前后的賦值語句來進行分配操作數的計算的，然后假設n無窮大時，看看哪一項對分配操作數的影響最大，一般是取高次項