題目鏈接:http://61.187.179.132/JudgeOnline/problem.php?id=2440
題意:給定K。求不是完全平方數(這里1不算完全平方數)的倍數的數字組成的數字集合S中第K小的數字是多少?
思路:首先,答案不超過2K,這個我看別人的知道的,我本以為答案會很大。。這樣二分就比較顯然了。二分之后就是判斷可行性。也就是求二分值n之內有多少個集合S中的數字。此時,我們可以反著想,就是計算有多少個數字不是S集合中的,也就是是完全平方數倍數的數字的個數。這個用容斥原理:
(1)加上一個的:n/4+n/9+n/25+……;
(2)減去兩個的:n/36+n/100+……;
就是這樣,但是這個容斥看起來我覺得復雜付還是蠻大的。下面說莫比烏斯函數:
利用莫比烏斯函數,我們直接求n之內有多少個是S集合中的:
?
int mou[N];
void init()
{
? ? i64 i,j;
? ? for(i=2;i<N;i++) if(!mou[i])
? ? {
? ? ? ? mou[i]=i;
? ? ? ? for(j=i*i;j<N;j+=i) mou[j]=i;
? ? }
? ? mou[1]=1;
? ? for(i=2;i<N;i++)
? ? {
? ? ? ? if(i%(mou[i]*mou[i])==0) mou[i]=0;
? ? ? ? else mou[i]=-mou[i/mou[i]];
? ? }
}
i64 n;
i64 cal(i64 n)
{
? ? i64 ans=0,i;
? ? for(i=1;i*i<=n;i++) if(mou[i]) ans+=mou[i]*n/i/i;
? ? return ans;
}
int main()
{
? ? init();
? ? rush()
? ? {
? ? ? ? RD(n);
? ? ? ? i64 low=1,high=inf,mid,ans;
? ? ? ? while(low<=high)
? ? ? ? {
? ? ? ? ? ? mid=(low+high)>>1;
? ? ? ? ? ? if(cal(mid)>=n) ans=mid,high=mid-1;
? ? ? ? ? ? else low=mid+1;
? ? ? ? }
? ? ? ? PR(ans);
? ? }
}

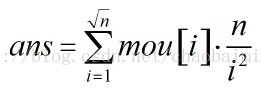






)









:視頻截圖)


