分塊入門

我貌似和所有的數據結構都有些誤會。。。。。。

在處理一些修改查詢問題的時候，我們可以利用分治的思想，比如說把一個線性的數據不斷分成一棵二叉樹，也就是我們所說的線段樹，這樣我們就可以在logn的時限里做到修改和查詢。同理我們也可以把數據分成一個只有兩層的樹（算上根節點三層），每個節點分成sqrt（該節點大小）個節點，這就是我們所說的分塊了。

這里我們主要講解分塊的思想：

話不多說先上一張圖：

?

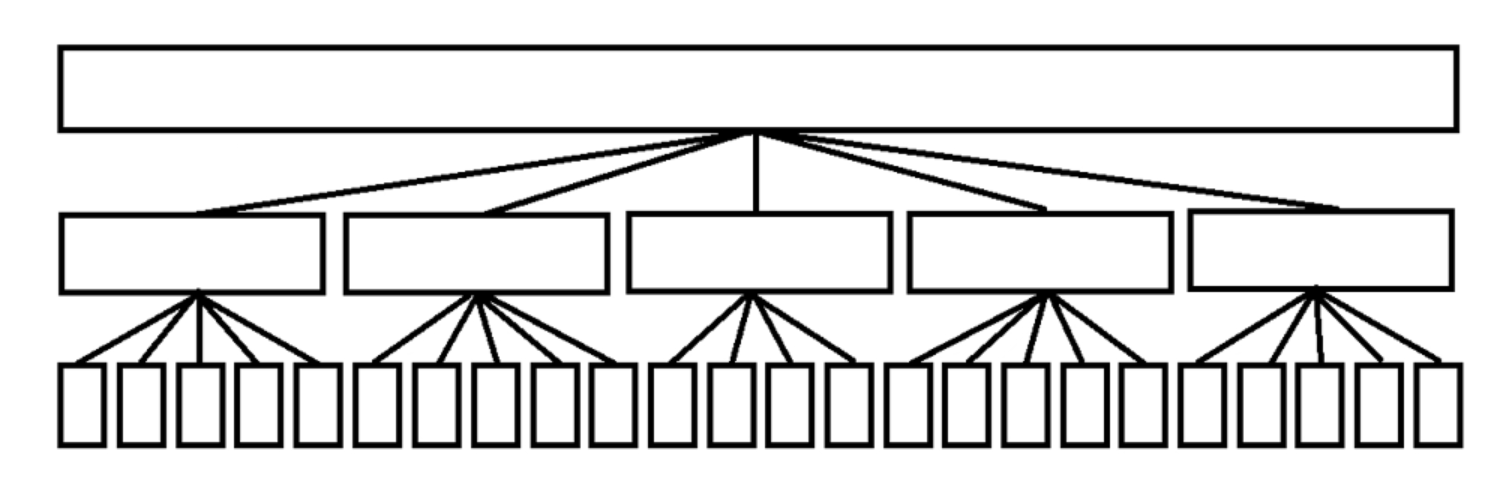
如圖，我們這就是一個分好塊的結構。

那么，這個結構有個什么用呢？很明顯，我們可以用它維護單點修改與查詢，區間的修改，查詢。。。

看上去有些眼熟，是不是，想起來了些什么？

沒錯，就是線段樹那幾個操作。那么現在我們繼續，可以發現分塊的修改和查詢操作都是O（sqrt（n））的。那還要分塊有個什么用？？

我們先來看這么一道題：

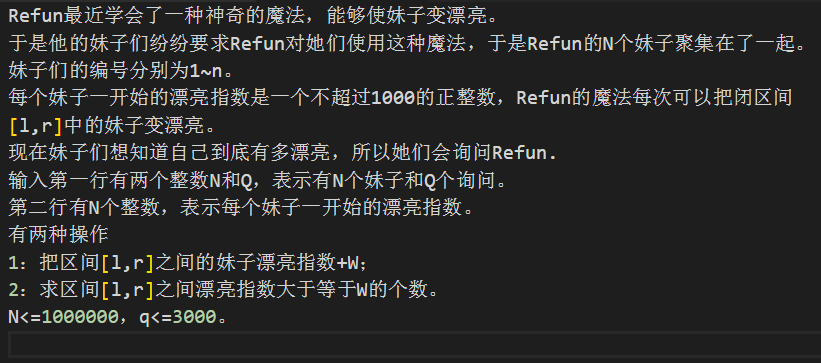
我們剛開始看的時候可能覺得可以用數據結構實現，什么線段樹主席樹平衡樹都可以想一想，不過一會你就會發現，它們都不可行，過了一會，你會發現有一種線段樹套平衡樹的方法或許可做，只不過代碼復雜度很高，而且估計要調不短的時間吧。這個時候就是分塊出場的時候了。

為什么這個題不能通過線段樹實現，原因就在于第二個操作過于煩人，線段樹維護的區間信息無法找出單點的，如果要查找一個區間中的所有點，無法得到一個讓人滿意的復雜度。那么為什么分塊就可以令人滿意了呢？？

首先我們說明幾個接下來經常會說的名詞：

整塊：查詢范圍內完全包括的塊，也就是范圍內第二層的塊。

零散塊：查詢范圍內除了整塊其他的部分，是第三層的塊，也就是一個一個的點。

接著聲明幾個變量：

那么我們再修改的時候，對于區間內所有的整塊，我們O(1)的打上加法標記即可。

?

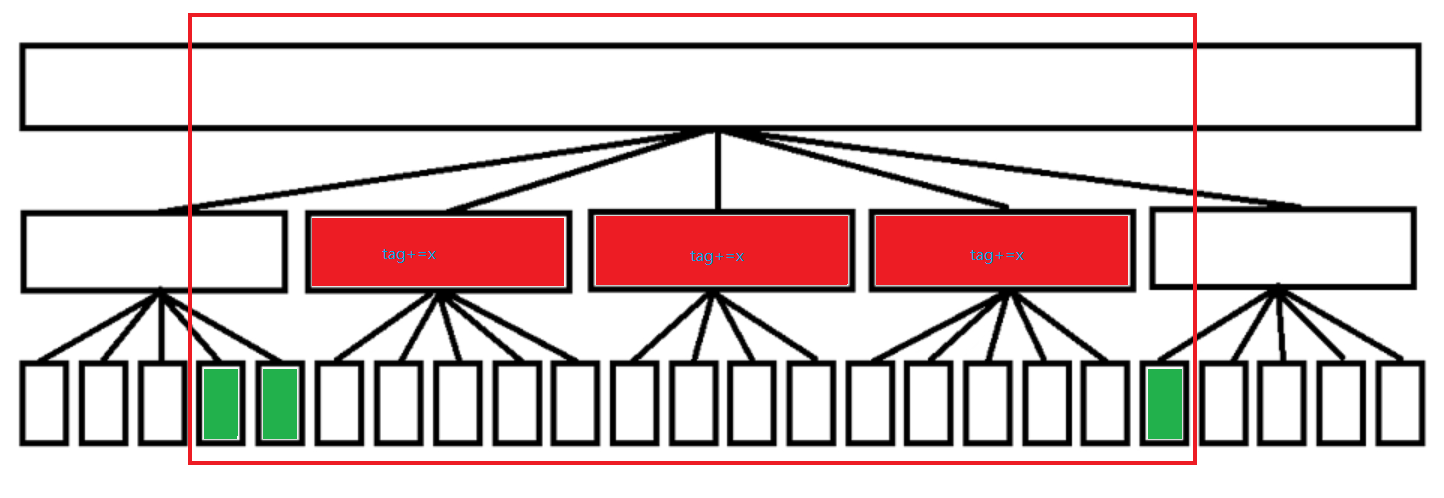
那么對于所有的零散塊呢？

?我們發現，我們最多有兩個部分的零散塊，其中每個部分里最多有不超過sqrt（n）個點，我們直接暴力枚舉下標修改即可，那么整個修改操作的復雜度就是O（sqrt（n））；

那么我們再查詢的時候，對于每個整塊，我們可以知道它是完全有序的，所以我們可以直接二分查找返回。對于零散塊，我們仍然選擇暴力枚舉，那么查詢操作的復雜度就是O（sqrt（nlogn））。

所以整個操作我們就可以在O（qsqrt（nlogn））的復雜度內完成了。

筆者秉承懂了算法不看模板的法則，自己手動實現了一下這個題目。接下來分塊講述一下代碼的意義：

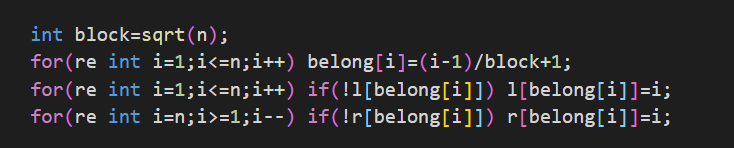
這一部分就是預處理并且分塊的部分，和塊的左右區間的處理。

然后在你的分塊主體開始之前，必須要有的一條語句：

這條語句就是先把b數組的每一個塊中的數據排好序，這樣要不然很有可能找的時候由于每一塊的b數組還沒有排序導致查找錯誤。

然后就是分塊的主體部分，我們分成修改和查詢分別看一下：

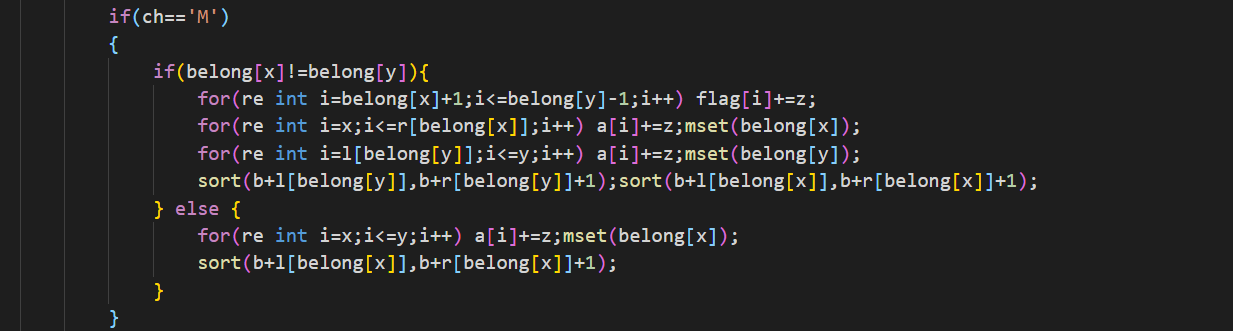
這個就是修改操作。要注意的是，在讀入的x和y點屬于同一個塊的時候我們要特殊操作。

如果不在同一個塊里，我們就遍歷包含的所有整塊，打上標記。然后對于左右那兩個零散塊，我們直接枚舉就可以了。為什么用的是a數組而不是b數組？因為b數組在排完序之后下標代表的意義是數的大小順序，而不是我們一開始讀入的順序，不能直接修改b數組。還有一個就是，這里筆者為了打上去方便，修改b數組的時候用了sort，這樣我們的復雜度就增加了一個sqrt（logn）但是我們使用歸并重構零散塊的話還是可以達到sqrt（n）的。對于 在同一個塊里的，我們也是直接暴力枚舉就可以了。

為什么這些零散塊可以暴力枚舉，復雜度不會很高么？不會的，在修改每一個零散塊的時候，我們最多也就修改sqrt（n）個點，所以并不會有特別高的額復雜度。

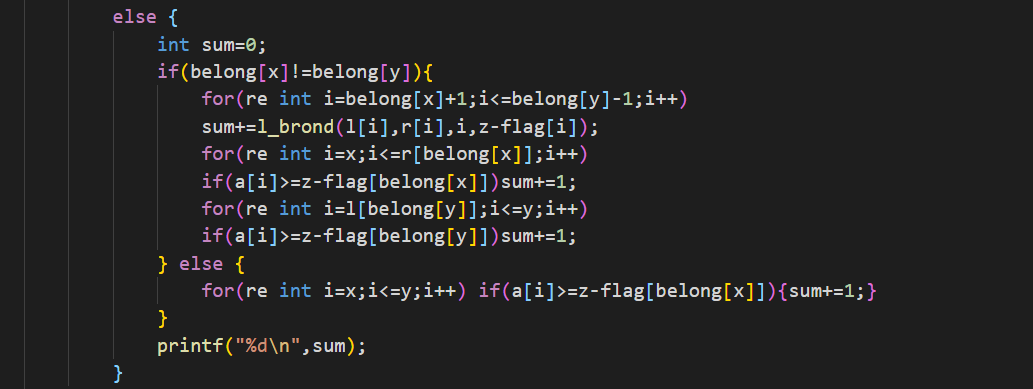
這個是查詢操作，怎么查找剛才都已經說過了，同樣零散塊我們就暴力枚舉即可。

那么這道題就這么完成了。

?純粹讓你用分塊完成的題目比較少，但是我們可以用這東西水一水分，畢竟這玩意比線段樹什么的好寫多了。

?