20172328 2018-2019《Java軟件結構與數據結構》第八周學習總結

概述 Generalization

本周學習了二叉樹的另一種有序擴展？是什么呢？你猜對了！ヾ(?°?°?)ﾉﾞ就是堆。本章將講解堆的鏈表實現and數組實現，以及往堆中添加元素或從堆中刪除元素的算法；還將介紹對的一些用途，包括基本使用和優先隊列。

教材學習內容總結 A summary of textbook

堆(heap)就是具有兩個附加屬性的一顆二叉樹:
- 第一點：它是一顆完全二叉樹，即葉子節點都在最后一層靠左側。
- 第二點：對每一結點，它小于(大于)或等于其左孩子和右孩子。
第二點中滿足大于的條件下形成的是一個最大堆（大頂堆），反之則為最小堆（小頂堆）。
最小堆將其最小元素存儲在該二叉樹的根處，且其跟的兩個孩子同樣還是最小堆。
堆中的操作：
addElement操作：
- addElement方法將給定的Comparable元素添加到堆的恰當位置處，且維持該堆的完全性屬性和有序屬性。
  - Little Tip：完全樹你還記得嗎？完全二叉樹就是所有葉子都位于h或者h-1層，其中h為log2（n），且n為樹中的元素數目，h層的所有葉子都位于該樹的左邊，那么該樹被認為是完全的。
- 堆就是一棵完全的二叉樹，所以對于插入的新結點只存在一個正確的位置。要么是h層左邊的下一個空位置，要么是h+1層左邊的第一個位置（如果h層為滿的話）。
- 將新結點定位到正確的位置后，我們就必須對這個堆進行排序來保持其有序屬性。方法就是對樹中的最末一片葉子進行跟蹤記錄，在一個addElement方法后，最末結點就被設定為插入結點。也就是通過上溯樹來保證樹的有序性.
removeMin操作：
- removeMin方法將刪除最小堆中的最小元素并返回它，由于最小元素是存儲在最小堆的根處，所以我們需要返回儲存在根處的元素并用堆中的另一元素替換它。
- 要維持該樹的完全性，就是把儲存在樹中最末一片葉子上的元素用來替換根元素。
- 將存儲在最末一片葉子上的元素移動到根處，就必須對該堆進行重新排序來維持該堆的排序屬性。
- 要維持該堆的排序屬性，就要從根結點下溯樹。具體過程是將該新根元素與其較小的孩子進行比較，且如果孩子更小就將它們互換，沿著樹向下繼續這一過程，直至該元素要么位于某一葉子中，要么比它的兩個孩子都小。
findMin操作：
- findMin將返回一個指向最小堆中最小元素的引用，由于最小堆的最小元素就在根處，所以直接返回存儲在根處的元素即可。
使用堆——堆排序heapSort：
- 堆排序是對簡單選擇排序的一種改進。
- 改進著眼點：如何減少關鍵字的比較次數
  - 簡單選擇排序在一趟排序中僅選出最小關鍵字，但是沒有把一趟比較結果保存下來，因而比較次數較多。
  - 堆排序在選出最小關鍵字同時，也找出較小的關鍵字，從而減少了后面選擇中的比較次數，提高了整個排序效率。
左右子樹都是大頂堆，如何調整根結點，使得整棵樹成為一個堆？
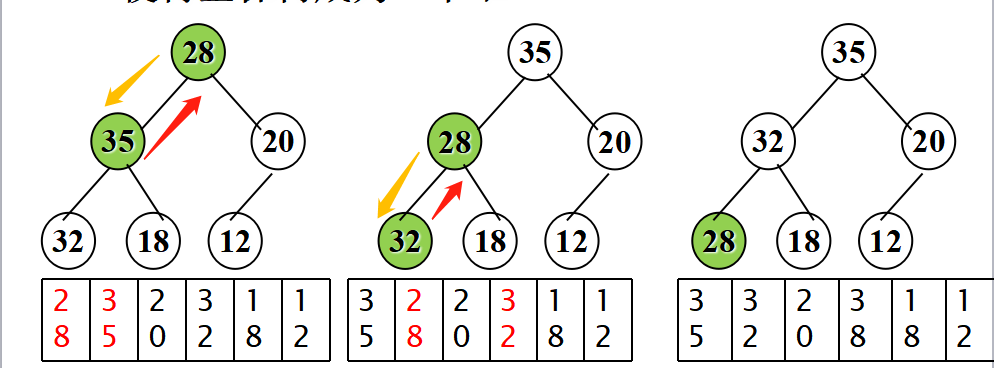
堆調整 —— 篩選過程
- 調整過程中，總是將根結點（被調整結點）與左右孩子比較；
- 不滿足堆條件時，將根結點與左右孩子中較大者交換；
- 這個調整過程一直進行到所有子樹都是堆或者交換到葉子為止。
- 這個從堆頂到葉子的調整過程稱為“篩選”。
對堆進行篩選完畢之后我們就要為保持其有序性而開始排序。
堆排序-排序過程
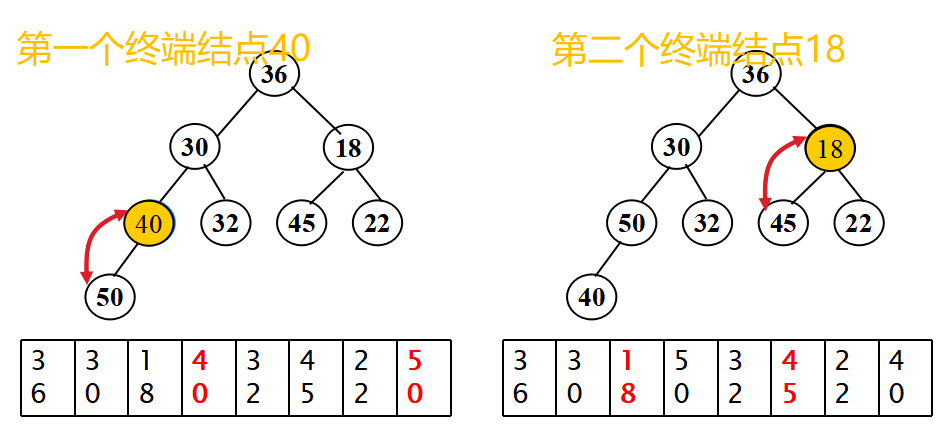
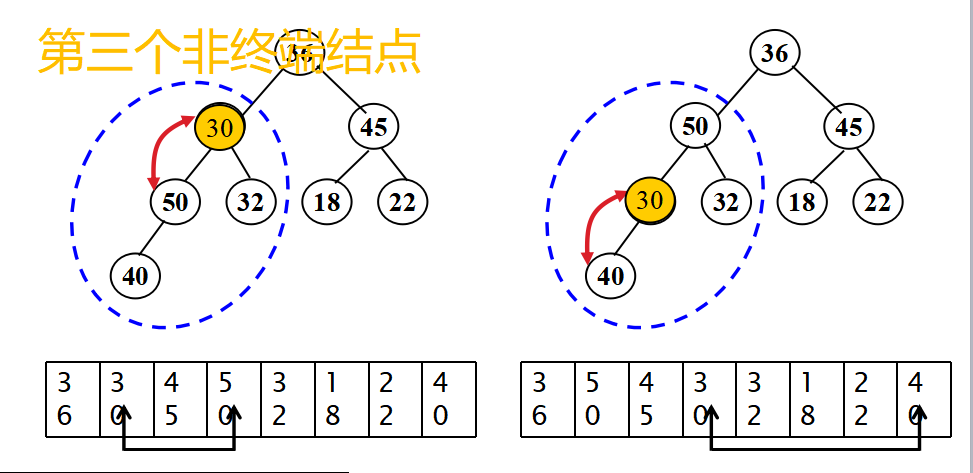
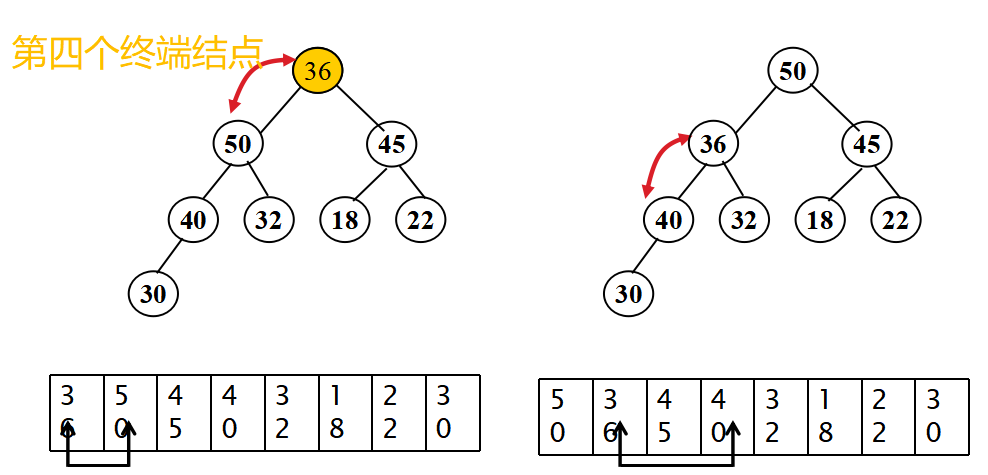
- 從無序序列的第[n/2]個元素開始（對應于完全二叉樹的最后一個非終端結點）進行篩選；
- 當解決一個非終端結點（非葉子結點）的有序問題后，把此非終端結點看做一個葉子，然后繼續上溯，找到倒數第二個非終端結點，繼續進行有序替換，知道整個堆有序為止。
heapSort的復雜度為O（nlogn）
使用堆：優先級隊列
優先級隊列（Priority queue）就是遵循兩個排序規則的集合。
- 首先，具有更高優先級的項目在先。
- 其次，具有相同優先級的項目使用先進先出方法來確定其排序。
  - Little Tip:雖然最小堆根本就不是一個隊列，但是它卻提供了一個高效的優先級隊列實現。
用鏈表實現堆：
- 因為我們要求在插入元素后能夠向上遍歷該樹，所以堆中的結點必須存儲在指向其雙親的指針。所以我們從創建一個HeapNode類開始我們的鏈表實現，該類對BinaryTreeNode進行了拓展并添加了一個雙親指針。
- 鏈表實現的實例數據由指向HeapNode且稱為lastNode的單個引用組成，這樣我們就能夠跟蹤記錄該堆中最末一片葉子。public HeapNode lastNode;
- addElement操作：
  - 在恰當的位置添加一個新元素
  - 對堆進行重排序以維持其排序屬性
  - 將lastNode指針重新設定指向新的最末結點
- removeMin操作：
  - 用存儲在最末結點處的元素替換存儲在根處的元素
  - 對堆進行重排序
  - 返回原始的根元素
- findMin操作：
  - 該方法僅僅返回一個指向存儲在堆根處元素的引用，因此復雜度為O（1）。
用數組實現堆：
- 用數組實現堆不再需要創建一個HeapNode類對，而是通過用數組來保存堆中的數據。
- 在二叉樹的數組實現中，樹的根位于位置0處，對于每一結點n，n的左孩子將位于數組的2n+1處，右孩子將位于數組的2n+2處。
- addElement操作：
  - 在恰當的位置添加一個新元素
  - 對堆進行重排序以維持其排序屬性
  - 將count遞增1.
- removeMin操作：
  - 用存儲在最末結點處的元素替換存儲在根處的元素
  - 對堆進行重排序
  - 返回原始的根元素
- findMin操作：
  - 返回指向存儲在堆的根處或數組0位置處的元素。
總結：鏈表實現和數組實現的addElement方法和removeElement方法時間復雜度都是O（logn）。但是，數組的實現還是更高效一些，因為在addElement操作中數組實現不用去確定插入雙親的結點，在removeElement操作中數組實現不需要確定新的最末一片葉子。

教材學習中的問題和解決過程 Problem and countermeasure

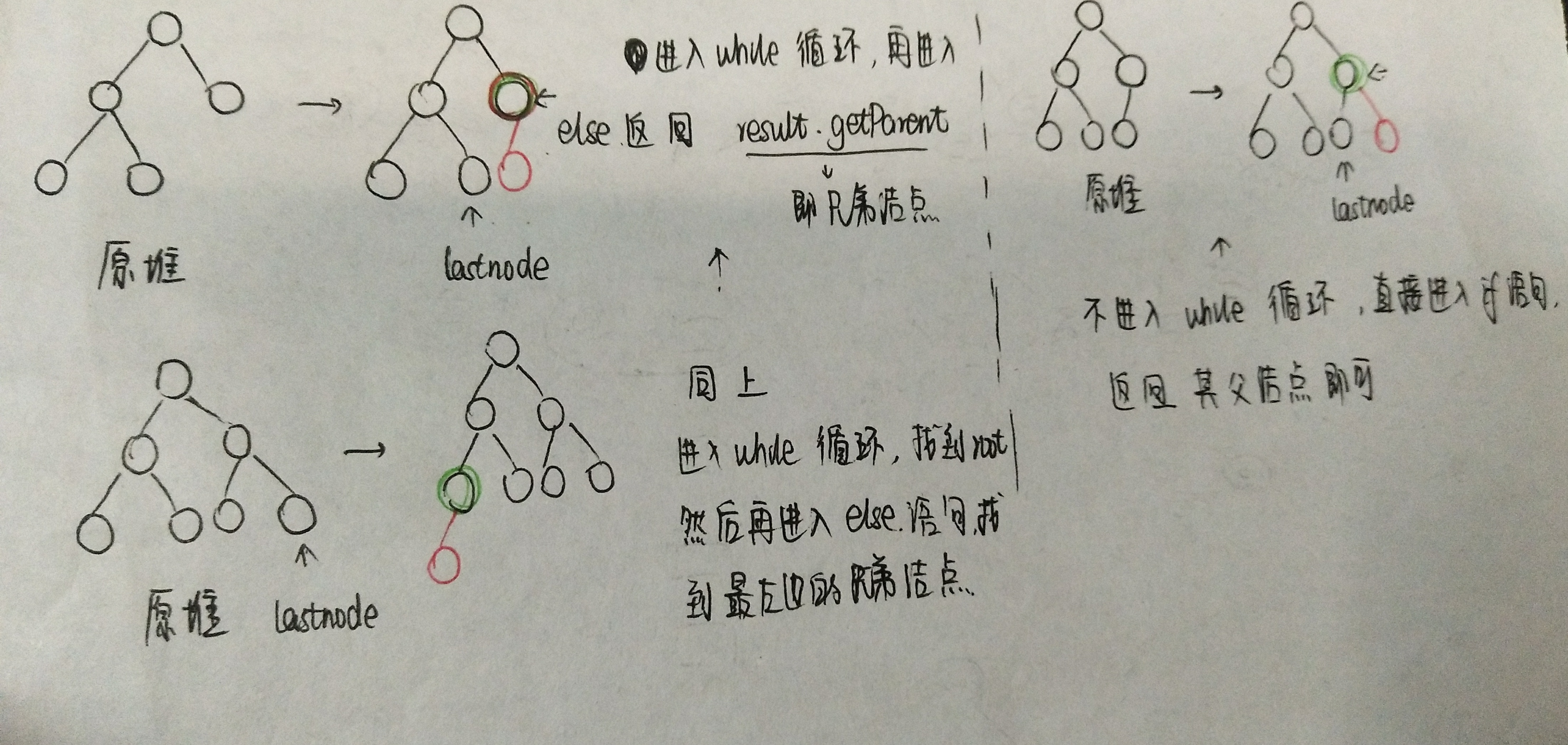
問題1：周四晚上看用鏈表實現堆的添加操作代碼。剛剛看懂小伙伴仇夏來找我討論，討論了一會瞬間覺得自己沒有真正看懂，那段奇妙的代碼如下：

private HeapNode<T> getNextParentAdd(){HeapNode<T> result = lastNode;while ((result != root) && (result.getParent().getLeft() != result))result = result.getParent();if (result != root)if (result.getParent().getRight() == null)result = result.getParent();else{result = (HeapNode<T>)result.getParent().getRight();while (result.getLeft() != null)result = (HeapNode<T>)result.getLeft();}elsewhile (result.getLeft() != null)result = (HeapNode<T>)result.getLeft();return result;}

這段代碼是返回將要插入結點的雙親結點的方法，當時我和仇夏討論的是有兩種情況。因為我們知道插入操作為了保證樹的完全性，所以要在h層的從左開始數的第一個空結點插入或者在h+1層的最左邊插入（如果樹是滿的話），但是在循環體中不滿足我們的要求。

問題1的解決：
問題的重點是“下一個將要插入結點的雙親結點”,之前一直理解的是新插入結點的雙親結點，所以當然不對。在理解正確之后，畫出幾種插入的可能情況，再跟著上述代碼理解幾遍，就慢慢清晰明朗了。
問題2：之前在學習棧的時候感覺一直在和堆一起被提起，所以堆和棧之間到底是什么關系？
問題2的解決：
簡單的說： Java把內存劃分成兩種：一種是棧內存，一種是堆內存。
在函數中定義的一些基本類型的變量和對象的引用變量都在函數的棧內存中分配。當在一段代碼塊定義一個變量時，Java就在棧中為這個變量分配內存空間，當超過變量的作用域后，Java會自動釋放掉為該變量所分配的內存空間，該內存空間可以立即被另作他用。
堆內存用來存放由new創建的對象和數組。在堆中分配的內存，由Java虛擬機的自動垃圾回收器來管理。
堆和棧的區別比較：
- 1.棧(stack)與堆(heap)都是Java用來在Ram中存放數據的地方。與C++不同，Java自動管理棧和堆，程序員不能直接地設置棧或堆。
- 2.棧的優勢是，存取速度比堆要快，僅次于直接位于CPU中的寄存器。但缺點是，存在棧中的數據大小與生存期必須是確定的，缺乏靈活性。另外，棧數據可以共享，詳見第3點。堆的優勢是可以動態地分配內存大小，生存期也不必事先告訴編譯器，Java的垃圾收集器會自動收走這些不再使用的數據。但缺點是，由于要在運行時動態分配內存，存取速度較慢。
- 3.Java中的數據類型有兩種。一種是基本類型(primitive types), 共有8種，即int, short, long, byte, float, double, boolean, char(注意，并沒有string的基本類型)。這種類型的定義是通過諸如int a = 3; long b = 255L;的形式來定義的，稱為自動變量。值得注意的是，自動變量存的是字面值，不是類的實例，即不是類的引用，這里并沒有類的存在。如int a = 3; 這里的a是一個指向int類型的引用，指向3這個字面值。這些字面值的數據，由于大小可知，生存期可知(這些字面值固定定義在某個程序塊里面，程序塊退出后，字段值就消失了)，出于追求速度的原因，就存在于棧中。

代碼實現時的問題作答 Exercise

問題1：用堆實現隊列？樹中給的堆是由數組和鏈表實現的,那么我們應該用ArrayHeap還是Linkedheap實現呢？又該如何實現？
問題1的解決：首先，我們知道在第十章中隊列的實現可以由鏈表或者循環數組實現，并且堆可以由鏈表和數組實現，因此是否可以推出隊列可以由數組實現的堆或者鏈表實現的堆來實現呢？
首先，我先用鏈表實現的堆來實現隊列。通過在enqueue方法中調用addElement方法，就能夠實現隊列的入隊，但是在入隊后進行了堆的插入中的排序？隊列是符合先進先出原則的，那么我就修改了堆中的插入方法，將其中的排序刪掉。同理，當出隊時也不應該去考慮排序的問題。但是當我刪除掉刪除的排序后，再執行刪除隊列中前兩個元素，我卻發現刪除的并不一定是隊列的前兩個值，反而刪除掉了最開始跟的值和最末一個葉子，這是由堆的性質決定的。所以想要保持先進先出，我們就要找到堆頂的左孩子然后刪除。所以我們需要改變一下堆中的排序方法。鏈表的實現方法很麻煩，而且要改變刪除的排序算法需要考慮很多種情況，在做了兩小時還是不能完整正確的情況下，讓我們把目光投向數組。
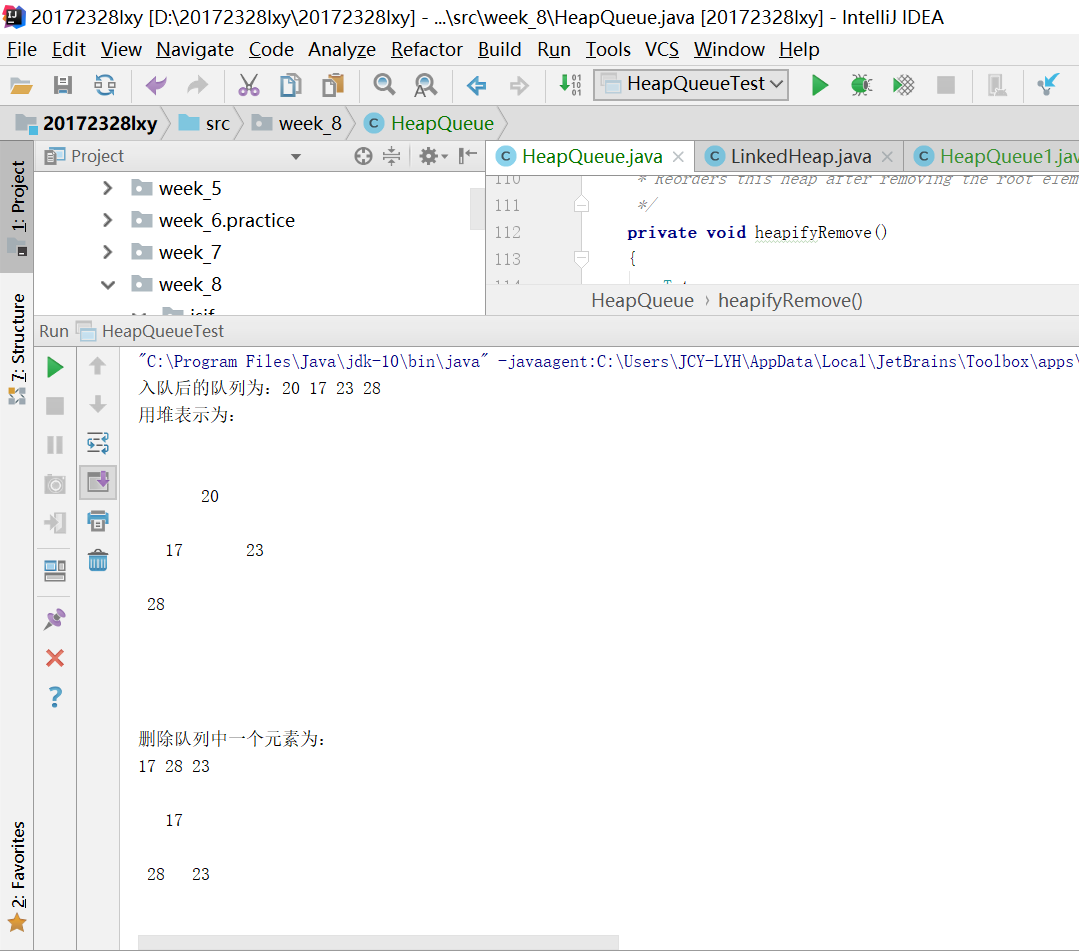
數組中只需要將刪除后的最末結點變成null就可以達到效果。

上周測試活動錯題改正 Correction

1.In removing an element from a binary search tree, another node must be ___________ to replace the node being removed.
A .duplicated
B .demoted
C .promoted
D .None of the above
正確答案選 B。當在二叉查找樹上刪除一個結點時，后面的結點需要向上移動來補全。當時，以為越靠近根結點說明深度越低，所以是降級了；但是看完答案好像人家的意思是向上補全。題意理解不準確哈哈
2.In removing an element from a binary search tree, another node must be demoted to replace the node being removed.
A .True
B .Flase
正確答案選 A ，和第一題一模一樣好嗎？哭
3.One of the uses of trees is to provide simpler implementations of other collections.
A .True
B .Flase
正確答案選 B 。這道題確實是我自己不太懂的。通過搜索得知，java中樹的應用主要有：菜單樹，還有權限樹，商品分類列表也是樹結構。在這幾章的學習中，好像確實沒有通過樹來簡單實現其他集合，樹提供的方便性可以用于查找、排序等等。
4.Insertion sort is an algorithm that sorts a list of values by repetitively putting a particular value into its final, sorted, position.
A .true
B .false
正確答案選 B ，我當時選了A。我覺得還是題意理解的問題。我理解的題意是“插入排序是一種重復的將特殊值插入后面，然后排序，然后安置的算法”我覺得插入排序就是這樣一個流程，所以我也不知道出現了什么問題。

碼云鏈接

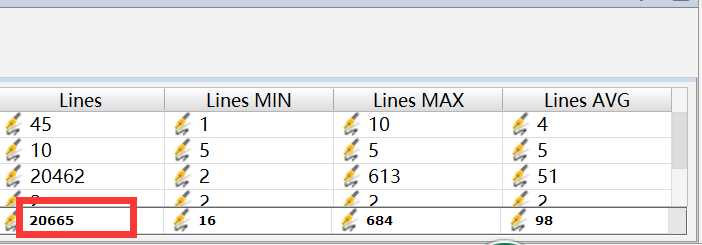
代碼量（截圖）

結對及互評Group Estimate

點擊進入結對小伙伴20172301郭愷的博客
點擊進入結對小伙伴20172304段志軒的博客

點評模板：

博客中值得學習的或問題：
- 20172301：這周的實驗四完全沒有思路，是最后看了郭愷同學的作業勉強理解了然后寫的。所以說，佩服佩服。對鏈表堆和數組堆的優缺點分析的很透徹。
- 20172304：圖很多，但是排版有點混亂，不是特別美觀可以繼續改進。內容還是有點少，沒有上周博客好喲！一起繼續加油！

其他（感悟、思考等，可選）Else

Crossing miles of frustrations and rivers a raging,picking up stones I found along the way.

怕不輕松，怕太輕松。
再也不用覺得工作日長，因為每天好像都是工作日。想忙里偷閑就忙里偷閑，想抓緊做事就抓緊做事。

我將每天告訴自己：請對專業課程更加虔誠一點。

學習進度條Learning List

	代碼行數（新增/累積）	博客量（新增/累積）	學習時間（新增/累積）
目標	5000行	30篇	400小時
第一周	0/0	1/1	8/8
第二周	621/621	1/2	12/20
第三周	678/1299	1/3	10/30
第四周	2734/4033	1/4	20/50
第五周	1100/5133	1/5	20/70
第六周	1574/6707	2/7	15/85
第七周	1803/8510	1/8	20/105
第八周	2855/11365	2/10	25/130