一些奇妙的線段樹操作

學過數據結構和會做題完全是兩個概念orz

各種各樣的題目都應該見識一下

簡單的目錄：

最大連續長度

吉司機線段樹

線段樹合并/分裂

最大連續長度問題

典型題目：HDU 3911?（$Black$ $And$ $White$）

題目大意：有一個長度為$n$（$1\le n\le 10^5$）的$01$序列$a_i$，現在有$m$個操作：將區間$[l_i,r_i]$反轉（$01$互換），或詢問區間$[l_i,r_i]$中$1$最多連續出現多少次

區間的反轉很顯然可以用懶標記解決，細節就不再贅述了（比如打完標記向上更新啥的一開始我就忘了orz）

難辦的是區間內的最大連續長度，原因在于，兩段小區間如何合并成一個大區間并不容易想到

先考慮最大連續長度可能的來源

僅在左半區間
僅在右半區間
橫跨兩個小區間

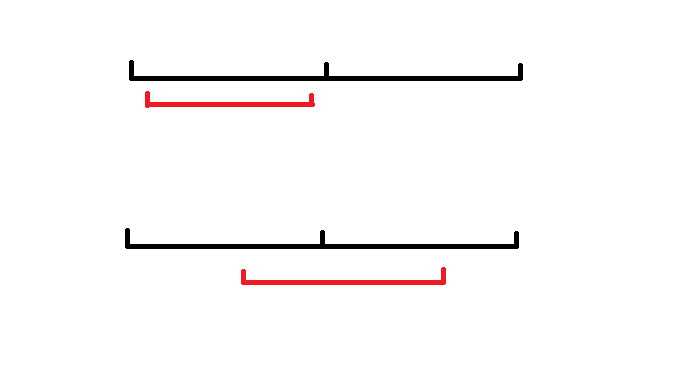
我們可以多記錄一東西：除了當前區間內的最大連續長度，再記錄當前區間內從最左端、最右端開始的最大連續長度

這樣，如果我們想把兩個小區間合并，得到的連續長度相當于是（左半區間從右端開始的最大長度+右半區間從左端開始的最大長度）

這兩個新加的記錄值也是容易合并的：求最左端開始的最大連續長度，如果左半區間全是相同數字，那么可以與右半區間的最左端合并，否則就是左半區間的最大連續長度；求最右端開始的亦是如此

所以本題的啟示是，加入一些新的記錄值來幫助計算

#include <cstdio>
#include <cmath>
#include <cstring>
#include <cstdlib>
using namespace std;inline int max(int a,int b)
{return (a>b?a:b);
}
inline int min(int a,int b)
{return (a<b?a:b);
}
inline void swap(int &a,int &b)
{int tmp=a;a=b,b=tmp;
}const int MAX=100005;int n,m;
int c[MAX<<1];int sz;
int left[MAX<<2][2],right[MAX<<2][2],mid[MAX<<2][2];
int tag[MAX<<2];inline void Calc(int k,int a,int b)
{int len=(b-a+1)>>1;for(int i=0;i<2;i++){left[k][i]=left[k<<1][i]+(left[k<<1][i]==len?left[(k<<1)+1][i]:0);right[k][i]=right[(k<<1)+1][i]+(right[(k<<1)+1][i]==len?right[k<<1][i]:0);mid[k][i]=max(mid[k<<1][i],mid[(k<<1)+1][i]);//#1mid[k][i]=max(mid[k][i],right[k<<1][i]+left[(k<<1)+1][i]);}
}inline void Build(int k,int a,int b)
{if(a==b){left[k][c[a]]=right[k][c[a]]=mid[k][c[a]]=1;return;}Build(k<<1,a,(a+b)>>1);Build((k<<1)+1,((a+b)>>1)+1,b);Calc(k,a,b);
}inline void Update(int k,int a,int b)
{if(!tag[k])return;swap(left[k][0],left[k][1]);swap(right[k][0],right[k][1]);swap(mid[k][0],mid[k][1]);tag[k]=0;if(a!=b){tag[k<<1]^=1;tag[(k<<1)+1]^=1;}
}inline void Modify(int k,int l,int r,int a,int b)
{Update(k,a,b);if(a>r || b<l)return;if(a>=l && b<=r){tag[k]^=1;Update(k,a,b);return;}Modify(k<<1,l,r,a,(a+b)>>1);Modify((k<<1)+1,l,r,((a+b)>>1)+1,b);Calc(k,a,b);
}inline int Query(int k,int l,int r,int a,int b)
{Update(k,a,b);if(a>r || b<l)return 0;if(a>=l && b<=r)return mid[k][1];int half=(a+b)>>1;if(r<=half)return Query(k<<1,l,r,a,half);if(l>half)return Query((k<<1)+1,l,r,half+1,b);int midv=max(Query(k<<1,l,r,a,half),Query((k<<1)+1,l,r,half+1,b));midv=max(midv,min(right[k<<1][1],half-l+1)+min(left[(k<<1)+1][1],r-half));return midv;
}int main()
{
//    freopen("input.txt","r",stdin);while(~scanf("%d",&n)){memset(left,0,sizeof(left));memset(right,0,sizeof(right));memset(mid,0,sizeof(mid));memset(tag,0,sizeof(tag));memset(c,0,sizeof(c));for(int i=1;i<=n;i++)scanf("%d",&c[i]);sz=1;while(sz<n)sz<<=1;Build(1,1,sz);scanf("%d",&m);while(m--){int op,x,y;scanf("%d%d%d",&op,&x,&y);if(op==1)Modify(1,x,y,1,sz);elseprintf("%d\n",Query(1,x,y,1,sz));}}return 0;
}

View Code

吉司機線段樹

這種做法有一種明顯的標志：有一種操作是用$min(a_i,w)$來取代$a_i$

經典模板題：HDU 5306（$Gorgeous$ $Sequence$）

感謝這篇題解：https://www.cnblogs.com/shenben/p/6641984.html

做法的精髓是，不僅記錄當前節點表示的區間中的最大值$x$和區間和$sum$（不然只是普通的線段樹了），同時記錄區間中最大值的出現次數$cnt$和嚴格次大值$y$

現在我們考慮如何處理題目中的$0$修改

首先通過遞歸，定位到某個嚴格包含在區間中的線段$t_k$，然后根據具體情況分為三種處理方式

$t[k].x\le w$，即區間內的最大值也小于$w$，那么區間內的所有元素都不會改變，直接退出即可
$t[k].y<w<t_k.x$，即區間內僅有最大值大于$w$，那么區間內的$t[k].cnt$個最大值都需要變成$w$，同時對$t[k].sum$做出更新（$t[k].sum-=t[k].cnt\times (t[k].x-w)$，注意強制轉換成long long）
$t[k].y\le w$，即區間內有超過一種值大于等于$w$（如果$t[k].y==w$歸于第2類，那么$t[k].cnt$不會更新），無法直接更新，需要向下繼續遞歸結束后再重新計算來更新

同時我們發現，所有的更新僅限于第$2$類，其并沒有進行到底，所以每個節點的$t[k].x$都有類似懶標記的作用，在修改與查詢的過程中應當將這個懶標記向下更新

這個做法的復雜度沒找到推導...雖然有人說$O(NlogN)$，但還是覺得$O(N(logN)^2)$更靠譜點

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;typedef long long ll;
const int MAX=1000005;struct Node
{int x,y,cnt;ll sum;Node(int a=0,int b=0,int c=-1,ll d=0LL){x=a,y=b,cnt=c,sum=d;}
};int n,m;
int val[MAX<<1];
Node t[MAX<<2];inline void Update(int k)
{int left=k<<1,right=left+1;t[k].sum=t[left].sum+t[right].sum;if(t[left].x==t[right].x){t[k].x=t[left].x;t[k].y=max(t[left].y,t[right].y);t[k].cnt=t[left].cnt+t[right].cnt;}else{if(t[left].x<t[right].x)swap(left,right);t[k].x=t[left].x;t[k].y=max(t[left].y,t[right].x);t[k].cnt=t[left].cnt;}
}inline void Build(int k,int a,int b)
{if(a==b){t[k]=Node(val[a],-1,1,val[a]);return;}Build(k<<1,a,(a+b)>>1);Build((k<<1)+1,((a+b)>>1)+1,b);Update(k);
}inline void Dec(int k,int x)
{if(t[k].x<=x)return;t[k].sum-=(ll)t[k].cnt*(t[k].x-x);t[k].x=x;
}inline void Pushdown(int k)
{Dec(k<<1,t[k].x);Dec(k<<1|1,t[k].x);
}inline void Modify(int k,int l,int r,int a,int b,int w)
{if(a>r || b<l)return;if(a>=l && b<=r)//***
    {if(t[k].x<=w)return;if(t[k].y<w)//***
        {Dec(k,w);return;}}Pushdown(k);Modify(k<<1,l,r,a,(a+b)>>1,w);Modify(k<<1|1,l,r,((a+b)>>1)+1,b,w);Update(k);
}inline int Max(int k,int l,int r,int a,int b)
{if(a>r || b<l)return 0;if(a>=l && b<=r)return t[k].x;Pushdown(k);return max(Max(k<<1,l,r,a,(a+b)>>1),Max(k<<1|1,l,r,((a+b)>>1)+1,b));
}inline ll Sum(int k,int l,int r,int a,int b)
{if(a>r || b<l)return 0;if(a>=l && b<=r)return t[k].sum;Pushdown(k);return Sum(k<<1,l,r,a,(a+b)>>1)+Sum(k<<1|1,l,r,((a+b)>>1)+1,b);
}int main()
{
//    freopen("input.txt","r",stdin);int T;scanf("%d",&T);while(T--){scanf("%d%d",&n,&m);for(int i=1;i<=n;i++)scanf("%d",&val[i]);int sz=1;while(sz<n)sz<<=1;Build(1,1,sz);while(m--){int op,x,y,w;scanf("%d%d%d",&op,&x,&y);if(op==0){scanf("%d",&w);Modify(1,x,y,1,sz,w);}if(op==1)printf("%d\n",Max(1,x,y,1,sz));if(op==2)printf("%lld\n",Sum(1,x,y,1,sz));}for(int i=1;i<=n;i++)val[i]=0;for(int i=1;i<sz+n;i++)t[i]=Node();}return 0;
}

View Code

一道更加綜合的題：BZOJ 4695?（最假女選手）

這道題目就是上一題的加強版了，不僅有區間取$min$，還有區間加，區間取$max$

所以我們不僅要保存區間和、最大值、次大值、最大值出現次數，還要保存最小值、次小值、最小值出現次數、區間加的懶標記（貌似最后一個可以不用？有時間研究一下...）

雖然大家保存的節點結構都差不多，但后面的標記傳遞還是有點差距的（我的寫法雖然常數巨大，但是竟然能省略很多細節）

首先考慮區間加（操作$1$）

跟普通的線段樹區間加是一樣的操作：先定位，然后給$tag$加上這個數，并改變$sum$；每次將要訪問下層節點的時候，將$tag$向下傳遞

但是這道題中tag的存在感比普通的區間加中的要強很多，因為對于每個線段樹節點，最值、次最值都是相對值，真實的值需要加上這個節點的$tag$（這個在操作$2$、$3$出現）

然后是區間取$min$（操作$3$） <-跟上一題一樣，講起來方便

先遞歸到嚴格區間內，然后分三步操作（比較的時候記得加上$tag$）

但是這里存在比上一題麻煩的地方：修改區間最大、次大值的同時，我們還有可能改變區間的最小、次小值

別的大佬們在這里就直接討論了，但我寫的時候沒有想那么多（懷疑常數出現在這里）

我們先考慮一下，在什么時候才會從操作$3$的遞歸進入對單點的修改？

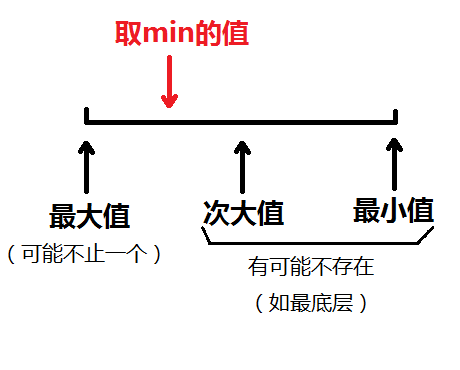
這下，最小、次小值改變的條件就清晰一些了

如果存在次小值，且最大值等于次小值，次小值改變，最小值不變
如果不存在次小值（即區間內全是最大值，此時最小值也是最大值），那么最小值改變，次小值仍不存在
否則（即次小值存在且小于最大值），最小值、次小值都不改變

區間取$max$（操作$2$）是這個的鏡像操作，別寫岔就行了

要記得將$tag$、小值、大值向下傳遞（與前一題差不多），并在遞歸后更新節點（我寫的巨丑，也是大常數的來源...有必要再學習一下別人的代碼）

這題跑了$46000+MS$，快反向登頂了，哎...

#include <cstdio>
#include <cstring>
#include <cmath>
#include <ctime>
#include <algorithm>
using namespace std;typedef long long ll;
const int MAX=500005;
const int INF=1<<30;struct Node
{ll sum;int tag,len;int fst[2],sec[2],cnt[2];Node(){fst[0]=sec[0]=-INF;fst[1]=sec[1]=INF;cnt[0]=cnt[1]=sum=tag=len=0;}Node(int x){fst[0]=fst[1]=x;sec[0]=-INF,sec[1]=INF;cnt[0]=cnt[1]=len=1;sum=x,tag=0;}
};int n,m,sz=1;
int val[MAX<<1];
Node t[MAX<<2];inline void Update(int k)
{Node l=t[k<<1],r=t[k<<1|1];t[k].sum=l.sum+r.sum;for(int i=0;i<2;i++){     l.fst[i]=l.fst[i]+l.tag-t[k].tag;l.sec[i]=l.sec[i]+l.tag-t[k].tag;r.fst[i]=r.fst[i]+r.tag-t[k].tag;r.sec[i]=r.sec[i]+r.tag-t[k].tag;if(l.fst[i]==r.fst[i]){t[k].fst[i]=l.fst[i];if(i==0)t[k].sec[i]=max(l.sec[i],r.sec[i]);elset[k].sec[i]=min(l.sec[i],r.sec[i]);t[k].cnt[i]=l.cnt[i]+r.cnt[i];}else{if(i==0 && l.fst[i]<r.fst[i])swap(l,r);if(i==1 && l.fst[i]>r.fst[i])swap(l,r);t[k].fst[i]=l.fst[i];if(i==0)t[k].sec[i]=max(l.sec[i],r.fst[i]);elset[k].sec[i]=min(l.sec[i],r.fst[i]);t[k].cnt[i]=l.cnt[i];}}
}inline void Build(int k,int r,int a,int b)
{if(a>r)return;if(a==b){t[k]=Node(val[a]);return;}Build(k<<1,r,a,(a+b)>>1);Build(k<<1|1,r,((a+b)>>1)+1,b);Update(k);t[k].len=t[k<<1].len+t[k<<1|1].len;
}inline void DecMax(int k,ll w)
{w-=t[k].tag;if(t[k].fst[0]<=w)return;t[k].sum-=(ll)t[k].cnt[0]*(t[k].fst[0]-w);if(t[k].fst[0]==t[k].sec[1])t[k].sec[1]=w;if(t[k].fst[0]==t[k].fst[1])t[k].fst[1]=w;t[k].fst[0]=w;
}inline void DecMin(int k,ll w)
{w-=t[k].tag;if(t[k].fst[1]>=w)return;t[k].sum-=(ll)t[k].cnt[1]*(t[k].fst[1]-w);if(t[k].fst[1]==t[k].sec[0])t[k].sec[0]=w;if(t[k].fst[1]==t[k].fst[0])t[k].fst[0]=w;t[k].fst[1]=w;
}inline void DecTag(int k)
{if(t[k].tag==0)return;for(int i=0;i<2;i++){t[k].fst[i]+=t[k].tag;t[k].sec[i]+=t[k].tag;}if(k<sz){t[k<<1].tag+=t[k].tag;t[k<<1].sum+=(ll)t[k].tag*t[k<<1].len;t[k<<1|1].tag+=t[k].tag;t[k<<1|1].sum+=(ll)t[k].tag*t[k<<1|1].len;}t[k].tag=0;
}inline void Down(int k)
{DecTag(k);DecMax(k<<1,t[k].fst[0]);DecMin(k<<1,t[k].fst[1]);DecMax(k<<1|1,t[k].fst[0]);DecMin(k<<1|1,t[k].fst[1]);
}inline void Add(int k,int l,int r,int a,int b,int w)
{if(a>r || b<l)return;if(a>=l && b<=r){t[k].tag+=w;t[k].sum+=(ll)t[k].len*w;return;}Down(k);Add(k<<1,l,r,a,(a+b)>>1,w);Add(k<<1|1,l,r,((a+b)>>1)+1,b,w);Update(k);
}inline void ModifyMax(int k,int l,int r,int a,int b,int w)
{if(a>r || b<l)return;if(a>=l && b<=r){if(t[k].fst[1]+t[k].tag>=w)return;if(t[k].sec[1]+t[k].tag>w){DecMin(k,w);return;}}Down(k);ModifyMax(k<<1,l,r,a,(a+b)>>1,w);ModifyMax(k<<1|1,l,r,((a+b)>>1)+1,b,w);Update(k);
}inline void ModifyMin(int k,int l,int r,int a,int b,int w)
{if(a>r || b<l)return;if(a>=l && b<=r){if(t[k].fst[0]+t[k].tag<=w)return;if(t[k].sec[0]+t[k].tag<w){DecMax(k,w);return;}}Down(k);ModifyMin(k<<1,l,r,a,(a+b)>>1,w);ModifyMin(k<<1|1,l,r,((a+b)>>1)+1,b,w);Update(k);
}inline ll QuerySum(int k,int l,int r,int a,int b)
{if(a>r || b<l)return 0LL;if(a>=l && b<=r)return t[k].sum;Down(k);return QuerySum(k<<1,l,r,a,(a+b)>>1)+QuerySum(k<<1|1,l,r,((a+b)>>1)+1,b);
}inline int QueryMax(int k,int l,int r,int a,int b)
{if(a>r || b<l)return -INF;if(a>=l && b<=r)return t[k].fst[0]+t[k].tag;Down(k);return max(QueryMax(k<<1,l,r,a,(a+b)>>1),QueryMax(k<<1|1,l,r,((a+b)>>1)+1,b));
}inline int QueryMin(int k,int l,int r,int a,int b)
{if(a>r || b<l)return INF;if(a>=l && b<=r)return t[k].fst[1]+t[k].tag;Down(k);return min(QueryMin(k<<1,l,r,a,(a+b)>>1),QueryMin(k<<1|1,l,r,((a+b)>>1)+1,b));
}int main()
{
//    freopen("input.txt","r",stdin);
//    freopen("my.txt","w",stdout); scanf("%d",&n);for(int i=1;i<=n;i++)scanf("%d",&val[i]);while(sz<n)sz<<=1;Build(1,n,1,sz);scanf("%d",&m);while(m--){int op,x,y,w;scanf("%d%d%d",&op,&x,&y);if(op<4)scanf("%d",&w);if(op==1)Add(1,x,y,1,sz,w);if(op==2)ModifyMax(1,x,y,1,sz,w);if(op==3)ModifyMin(1,x,y,1,sz,w);if(op==4)printf("%lld\n",QuerySum(1,x,y,1,sz));if(op==5)printf("%d\n",QueryMax(1,x,y,1,sz));if(op==6)printf("%d\n",QueryMin(1,x,y,1,sz));}return 0;
}

View Code

線段樹合并

這個一開始學起來真的有點困難...稍微有點抽象

在我的感覺中，是處理有關元素的有序性的問題的

例如將兩個區間$[1,8]$的統計元素出現次數的線段樹合并

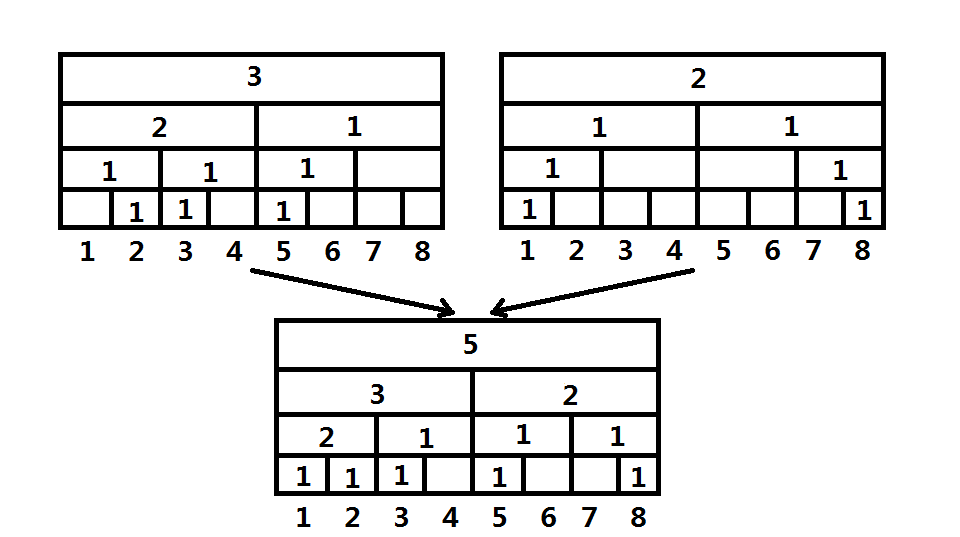
我們先想想如何實現

為了防止空間爆炸，我們寫的線段樹必然是動態開點的，那么便有一大優勢：可以類似可持久化線段樹一樣，通過將新節點的兒子指向已經存在的某節點來重復利用

在這個基礎上考慮將兩棵線段樹對于一個區間的兩個節點$x$、$y$合并成一個新節點

若$x$、$y$都為空，則合并后也為空
若$x$、$y$其中一個為空，那么可以直接指向不為空的節點（因為與空樹合并，原本的結構不變）
若$x$、$y$都不為空，那么分為左、右兒子繼續向下遞歸，最后在將左右的統計值相加

（其實還是有很多細節的，最好學習寫法比較好的代碼，比如后面引用到的）

這樣下來，復雜度是怎么樣的呢？

首先一般情況，如果一顆數值區間為$[1,n]$的線段樹是由$n$條鏈依次合并成的，那么就跟可持久化線段樹一樣，是$O(NlogN)$的時間復雜度

但是總有特例吧，比如下圖，兩棵線段樹在葉節點互補（意會一下）

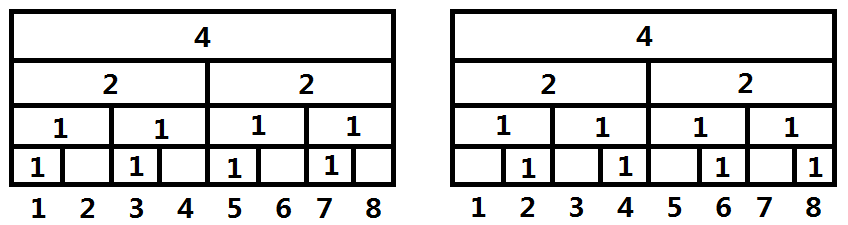
這樣的一次合并是$O(N)$的

但是不要著急，如果想構成這樣的情形，首先這兩個樹應當分別構造，且如果想讓單次合并的消耗盡量大，在葉節點處應當同樣互補

這樣總的算下來，時間復雜度是$O(N+2\times \frac{N}{2}+4\times \frac{N}{4}+...)=O(NlogN)$，可以放心食用

由于合并大多伴隨著開點，所以空間復雜度也是$O(NlogN)$，應當注意不要MLE

說了這么多，具體代碼怎么實現比較好，又有什么用呢？

且看這道題目：BZOJ 2212?（$POI2011$，$Tree Rotations$）

我完全看的是這篇題解：胡小兔：神奇的操作——線段樹合并（例題: BZOJ2212）

具體題目分析和代碼實現都無可挑剔，我就不做無用功了

但是僅僅做出這一道題離熟練掌握還差距很大

再來一道題目：BZOJ 4552 （$TJoi2016$ & $HEoi2016$，排序）

準備學習一下這份代碼：fjzzq2002：線段樹合并與分裂

這道題目更加綜合一些，不僅要求線段樹的合并，還有分裂

其實在掌握合并的基礎上，分裂也是容易處理的

加入我們想在以$root$為根的線段樹上將第$p$個元素（包含第$p$個）分裂成一顆新樹，就可以類似主席樹上找第$k$大的遞歸處理

對于當前節點$x$（$t_x$表示，節點$x$覆蓋的區間共有多少元素）

若$t_{l_i}\le p$，那么第$p$個元素一定在$x$的左兒子中，將$r_x$直接割給新樹
若$t_{l_i}>p$，那么第$p$個元素一定在$x$的右兒子中
若已經到達底端，則此時$x$就是以$root$為根的線段樹中第$p$個元素，將$x$割給新樹（在這里，我的實現是將$t_x$清零，將新樹中對于節點$t_{cur}$賦成$1$）

然后可以刪去一些分裂中被割走的節點：如果對于當前節點$x$，$t_{l_x}==0$，即左子樹為空，那么令$l_x=0$以免之后的合并訪問到這個沒必要經過的節點；對于$r_x$同理

在這題中，除去了線段樹的合并與分裂（總體應該是$O(NlogN)$，但是具體不會證），我們還需要一種數據結構告訴我們應該合并哪些線段樹

一開始的想法是用一顆區間賦值線段樹給合并后的每一段打上懶標記，但是如果想要從一段合并區間到另一段，感覺上需要在樹上累加，應該是$O(logN)$的跳轉，細節還很多

zzq給出的思路是用set，排序的依據是區間的左端點

這樣一來，我們對每次排序的$[op,x,y]$操作，能夠直接二分$O(logN)$的找出左右端點所在的合并區間，然后再通過$iterator$遍歷將線段樹合并

（不過我對set十分陌生，一開始將s.lower_bound(x)寫成lower_bound(s.begin(),s.end(),x)，應該是不能這樣用的）

他是set<int>，我寫的是set<pair<int,int> >，細節還非常的繁瑣...應當學習一下他的處理方法

除去set的部分，我的代碼還是能看的

#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <algorithm>
#include <set>
using namespace std;typedef pair<int,int> pii;
const int MAX=100005;
const int LOG=100;int tot;
int l[MAX*LOG],r[MAX*LOG],t[MAX*LOG],rev[MAX*LOG];inline int Build(int x,int a,int b)
{int cur=++tot;t[cur]=1;if(a==b)return cur;int mid=(a+b)>>1;if(x<=mid)l[cur]=Build(x,a,mid);elser[cur]=Build(x,mid+1,b);return cur;
}inline int Merge(int x,int y,int a,int b)
{if(!x || !y)return x+y;int cur=++tot,mid=(a+b)>>1;l[cur]=Merge(l[x],l[y],a,mid);r[cur]=Merge(r[x],r[y],mid+1,b);t[cur]=t[l[cur]]+t[r[cur]];return cur;
}inline void Update(int x)
{if(!t[l[x]])l[x]=0;if(!t[r[x]])r[x]=0;
}inline int Split(int x,int a,int b,int p)
{int cur=++tot,mid=(a+b)>>1;if(a==b){t[cur]=t[x];t[x]=0;return cur;}if(t[l[x]]>=p){l[cur]=Split(l[x],a,mid,p);r[cur]=r[x];r[x]=0;}elser[cur]=Split(r[x],mid+1,b,p-t[l[x]]);Update(x);Update(cur);t[x]=t[l[x]]+t[r[x]];t[cur]=t[l[cur]]+t[r[cur]];return cur;
}inline int Locate(int x,int a,int b,int p)
{if(a==b)return a;int mid=(a+b)>>1;if(t[l[x]]>=p)return Locate(l[x],a,mid,p);elsereturn Locate(r[x],mid+1,b,p-t[l[x]]);
}int n,m,sz=1;
int val[MAX];
set<pii> s;int main()
{
//    freopen("input.txt","r",stdin);
//    freopen("output.txt","w",stdout);scanf("%d%d",&n,&m);while(sz<n)sz<<=1;for(int i=1;i<=n;i++){scanf("%d",&val[i]);s.insert(pii(i,Build(val[i],1,sz)));}for(int i=1;i<=m;i++){int op,x,y;scanf("%d%d%d",&op,&x,&y);set<pii>::iterator beg=s.lower_bound(pii(x,0));if((*beg).first>x || beg==s.end())beg--;set<pii>::iterator end=s.lower_bound(pii(y,0));if((*end).first>y || end==s.end())end--;int idx1=(*beg).second,left1=(*beg).first,idx2=(*end).second,left2=(*end).first;if(idx1==idx2){s.erase(beg);int p1=x-left1+1,p2=y-left1+2;int rp1=t[idx1]-(x-left1)+1,rp2=t[idx1]-(y-left1);int left,right,mid;if(!rev[idx1]){left=idx1,mid=Split(idx1,1,sz,p1),right=Split(mid,1,sz,p2-p1+1);if(t[left])s.insert(pii(left1,left));if(t[right])s.insert(pii(y+1,right));s.insert(pii(x,mid));}else{left=idx1,mid=Split(idx1,1,sz,rp2),right=Split(mid,1,sz,rp1-rp2+1);if(t[left])s.insert(pii(y+1,left));if(t[right])s.insert(pii(left1,right));rev[left]=rev[right]=1;s.insert(pii(x,mid));}rev[mid]=op;continue;}int num1=left1+t[idx1]-x,num2=y-left2+1;int p1=t[idx1]-num1+1,p2=num2+1;int rp1=num1+1,rp2=t[idx2]-num2+1;int begn,endn,rem1,rem2,newn;if(!rev[idx1])begn=Split(idx1,1,sz,p1),rem1=idx1;elsebegn=idx1,rem1=Split(idx1,1,sz,rp1),rev[rem1]=1;//
        if(!rev[idx2])endn=idx2,rem2=Split(idx2,1,sz,p2);elseendn=Split(idx2,1,sz,rp2),rem2=idx2,rev[rem2]=1;//
        newn=Merge(begn,endn,1,sz);set<pii>::iterator it=beg;it++;while(it!=end)newn=Merge(newn,(*it).second,1,sz),it++;s.erase(beg,end);s.erase(end);if(t[rem1])s.insert(pii(left1,rem1));if(t[rem2])s.insert(pii(y+1,rem2));s.insert(pii(x,newn));rev[newn]=op;}int q;scanf("%d",&q);set<pii>::iterator it=s.lower_bound(pii(q,0));if((*it).first>q || it==s.end())//
        it--;int x=(*it).second,left=(*it).first;int p=(rev[x]?t[x]-(q-left):q-left+1);printf("%d\n",Locate(x,1,sz,p));return 0;
}

View Code

這題還有一種玩法是$O(N(logN)^2)$的二分+線段樹區間修改，網上大部分都是這樣的題解，也是一種有趣的思路吧

#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;const int MAX=100005;int n,m,q;
int val[MAX],op[MAX],ql[MAX],qr[MAX];
int c[MAX];int sz=1;
int t[MAX<<2],len[MAX<<2],tag[MAX<<2];inline void Build(int k,int l,int r)
{if(l==r){if(l<=n){t[k]=c[l];len[k]=1;}return;}int mid=(l+r)>>1;Build(k<<1,l,mid);Build(k<<1|1,mid+1,r);t[k]=t[k<<1]+t[k<<1|1];len[k]=len[k<<1]+len[k<<1|1];
}inline void Update(int x)
{if(!tag[x])return;t[x<<1]=(tag[x]>0?len[x<<1]:0);tag[x<<1]=tag[x];t[x<<1|1]=(tag[x]>0?len[x<<1|1]:0);tag[x<<1|1]=tag[x];tag[x]=0;
}inline int Query(int k,int l,int r,int a,int b)
{if(a>r || b<l)return 0;if(a>=l && b<=r)return t[k];Update(k);int mid=(a+b)>>1;return Query(k<<1,l,r,a,mid)+Query(k<<1|1,l,r,mid+1,b);
}inline void Add(int k,int l,int r,int a,int b,int w)
{if(a>r || b<l)return;if(a>=l && b<=r){tag[k]=w;t[k]=(w>0?len[k]:0);return;}Update(k);int mid=(a+b)>>1;Add(k<<1,l,r,a,mid,w);Add(k<<1|1,l,r,mid+1,b,w);t[k]=t[k<<1]+t[k<<1|1];//
}int Check(int x)
{memset(tag,0,sizeof(tag));for(int i=1;i<=n;i++)c[i]=(val[i]<=x);Build(1,1,sz);for(int i=1;i<=m;i++){int x=ql[i],y=qr[i],num=Query(1,x,y,1,sz);if(op[i]==0){Add(1,x,x+num-1,1,sz,1);Add(1,x+num,y,1,sz,-1);}else{Add(1,x,y-num,1,sz,-1);Add(1,y-num+1,y,1,sz,1);}}return Query(1,q,q,1,sz);
}int main()
{
//    freopen("input.txt","r",stdin);
//    freopen("output.txt","w",stdout);scanf("%d%d",&n,&m);while(sz<n)sz<<=1;for(int i=1;i<=n;i++)scanf("%d",&val[i]);for(int i=1;i<=m;i++)scanf("%d%d%d",&op[i],&ql[i],&qr[i]);scanf("%d",&q);int l=1,r=n,mid;while(l<r){mid=(l+r)>>1;if(Check(mid))r=mid;elsel=mid+1;}if(!Check(l))l++;printf("%d\n",l);return 0;
}