為什么學后綴數組
后綴數組是一個比較強大的處理字符串的算法,是有關字符串的基礎算法,所以必須掌握。?
學會后綴自動機(SAM)就不用學后綴數組(SA)了?不,雖然SAM看起來更為強大和全面,但是有些SAM解決不了的問題能被SA解決,只掌握SAM是遠遠不夠的。?
……
有什么SAM做不了的例子??
比如果求一個串后綴的lcp方面的應用,這是SA可以很方便的用rmq來維護,但是SAM還要求lca,比較麻煩,還有就是字符集比較大的時候SA也有優勢。
現在這里放道題,看完這個blog可能就會做了!:?
你可想想這道題:你有一個01串S,然后定義一個前綴最右邊的位置就是這個前綴的結束位置。現在有q多個詢問,每個詢問結束位置在l~r中不同前綴的最長公共后綴是多長??
|S|,q≤100000|S|,q≤100000?
時限4s
而下面是我對后綴數組的一些理解
構造后綴數組——SA
先定義一些變量的含義
Str :需要處理的字符串(長度為Len)?
Suffix[i] :Str下標為i ~ Len的連續子串(即后綴)?
Rank[i] : Suffix[i]在所有后綴中的排名?
SA[i] : 滿足Suffix[SA[1]] < Suffix[SA[2]] …… < Suffix[SA[Len]],即排名為i的后綴為Suffix[SA[i]] (與Rank是互逆運算)?
好,來形象的理解一下?
后綴數組指的就是這個SA[i],有了它,我們就可以實現一些很強大的功能(如不相同子串個數、連續重復子串等)。如何快速的到它,便成為了這個算法的關鍵。而SA和Rank是互逆的,只要求出任意一個,另一個就可以O(Len)得到。?
現在比較主流的算法有兩種,倍增和DC3,在這里,就主要講一下稍微慢一些,但比較好實現以及理解的倍增算法(雖說慢,但也是O(Len logLen))的。
進入正題——倍增算法
倍增算法的主要思想?:對于一個后綴Suffix[i],如果想直接得到Rank比較困難,但是我們可以對每個字符開始的長度為2k2k的字符串求出排名,k從0開始每次遞增1(每遞增1就成為一輪),當2k2k大于Len時,所得到的序列就是Rank,而SA也就知道了。O(logLen)枚舉k?
這樣做有什么好處呢??
設每一輪得到的序列為rank(注意r是小寫,最終后綴排名Rank是大寫)。有一個很美妙的性質就出現了!第k輪的rank可由第k - 1輪的rank快速得來!?
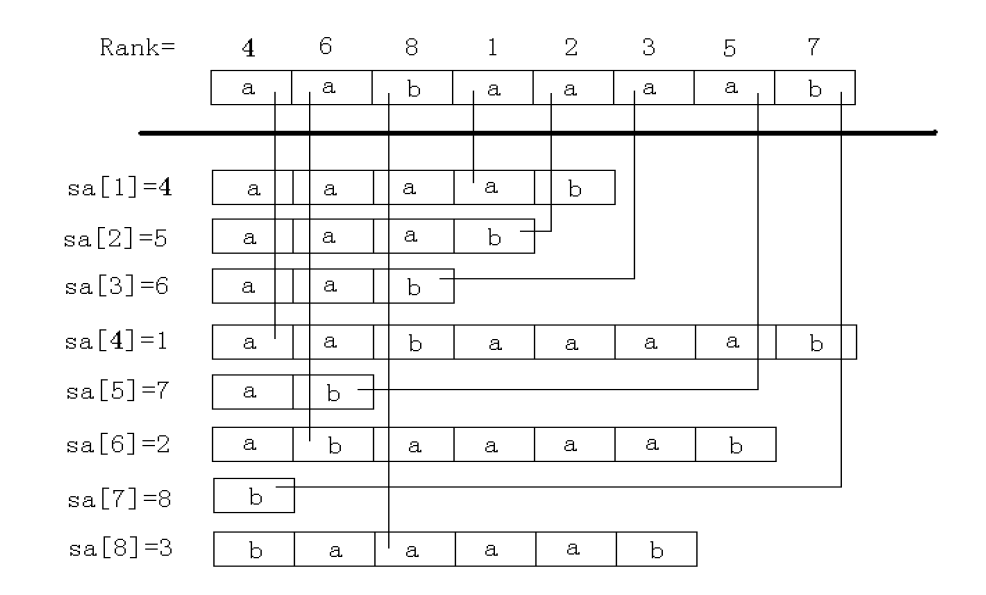
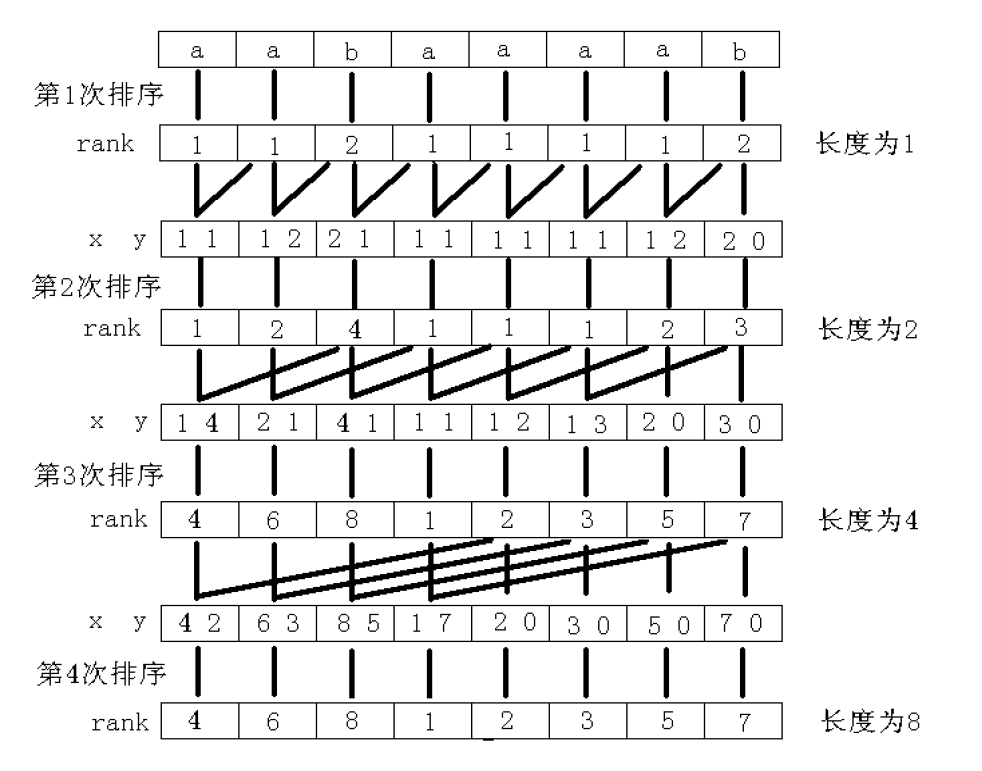
為什么呢?為了方便描述,設SubStr(i, len)為從第i個字符開始,長度為len的字符串我們可以把第k輪SubStr(i,?2k2k)看成是一個由SubStr(i,?2k?12k?1)和SubStr(i +?2k?12k?1,?2k?12k?1)拼起來的東西。類似rmq算法,這兩個長度而2k?12k?1的字符串是上一輪遇到過的!當然上一輪的rank也知道!那么吧每個這一輪的字符串都轉化為這種形式,并且大家都知道字符串的比較是從左往右,左邊和右邊的大小我們可以用上一輪的rank表示,那么……這不就是一些兩位數(也可以視為第一關鍵字和第二關鍵字)比較大小嗎!再把這些兩位數重新排名就是這一輪的rank。?
我們用下面這張經典的圖理解一下:?
相信只要理解字符串的比較法則(跟實數差不多),理解起來并不難。#還有一個細節就是怎么把這些兩位數排序?這種位數少的數進行排序毫無疑問的要用一個復雜度為長度*排序數的個數的優美算法——基數排序(對于兩位數的數復雜度就是O(Len)的)。?
基數排序原理?: 把數字依次按照由低位到高位依次排序,排序時只看當前位。對于每一位排序時,因為上一位已經是有序的,所以這一位相等或符合大小條件時就不用交換位置,如果不符合大小條件就交換,實現可以用”桶”來做。(敘說起來比較奇怪,看完下面的代碼應該更好理解,也可以上網查有關資料)?
好了SA和Rank(大寫R)到此為止就處理好了。(下面有詳解代碼!)。但我們發現,只有這兩樣東西好像沒什么用,為了處理重復子串之類的問題,我們就要引入一個表示最長公共前綴的新助手Height數組!
構造最長公共前綴——Height
同樣先是定義一些變量
Heigth[i] : 表示Suffix[SA[i]]和Suffix[SA[i - 1]]的最長公共前綴,也就是排名相鄰的兩個后綴的最長公共前綴?
H[i] : 等于Height[Rank[i]],也就是后綴Suffix[i]和它前一名的后綴的最長公共前綴?
而兩個排名不相鄰的最長公共前綴定義為排名在它們之間的Height的最小值。?
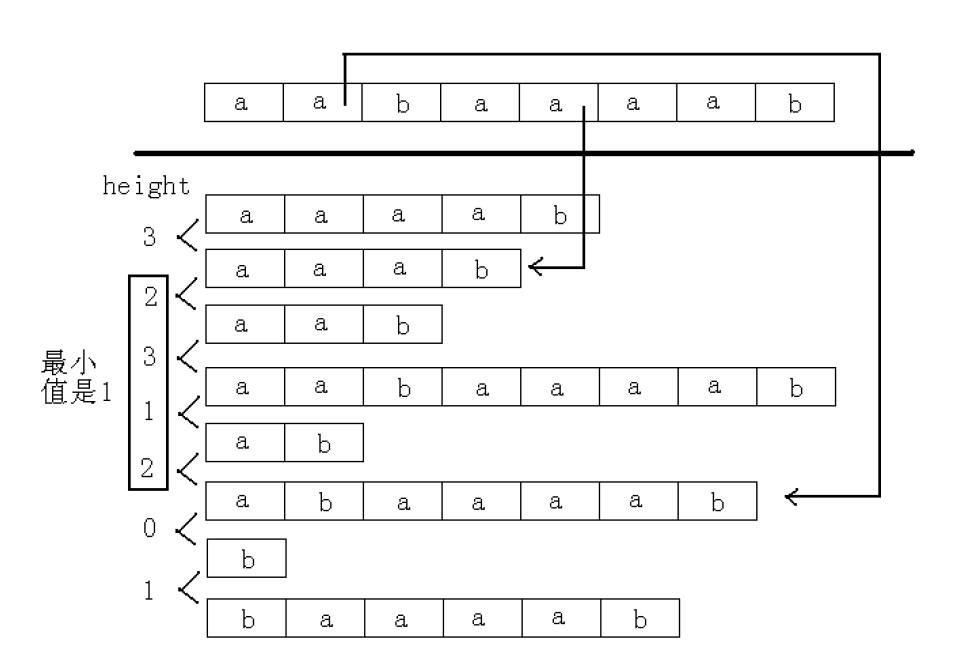
跟上面一樣,先形像的理解一下:?
高效地得到Height數組
如果一個一個數按SA中的順序比較的話復雜度是O(N2N2)級別的,想要快速的得到Height就需要用到一個關于H數組的性質。?
H[i] ≥ H[i - 1] - 1!?
如果上面這個性質是對的,那我們可以按照H[1]、H[2]……H[Len]的順序進行計算,那么復雜度就降為O(N)了!?
讓我們嘗試一下證明這個性質?: 設Suffix[k]是排在Suffix[i - 1]前一名的后綴,則它們的最長公共前綴是H[i - 1]。都去掉第一個字符,就變成Suffix[k + 1]和Suffix[i]。如果H[i - 1] = 0或1,那么H[i] ≥ 0顯然成立。否則,H[i] ≥ H[i - 1] - 1(去掉了原來的第一個,其他前綴一樣相等),所以Suffix[i]和在它前一名的后綴的最長公共前綴至少是H[i - 1] - 1。?
仔細想想還是比較好理解的。H求出來,那Height就相應的求出來了,這樣結合SA,Rank和Height我們就可以做很多關于字符串的題了!
代碼——Code


1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 const int N=100010; 6 int n,m,rank[N],sa[N],buc[N],id[N],height[N]; 7 char s[N]; 8 /*------------------------------------------------------------ 9 rank[i] 第i個后綴的排名; 10 sa[i] 排名為i的后綴位置; 11 buc[i] 計數排序輔助數組; 12 height[i] 排名為i的后綴與排名為(i-1)的后綴的LCP; 13 id[i] 倍增中后半段字符串位置(計數排序中的第二關鍵字); 14 s為原串 15 ------------------------------------------------------------*/ 16 inline void qsort(){ 17 //rank第一關鍵字,id第二關鍵字。 18 for(int i=0;i<=m;++i) buc[i]=0; 19 for(int i=1;i<=n;++i) ++buc[rank[id[i]]]; 20 for(int i=1;i<=m;++i) buc[i]+=buc[i-1]; 21 for(int i=n;i>=1;--i) sa[buc[rank[id[i]]]--]=id[i]; 22 //計數排序,把新的二元組排序 23 } 24 //通過二元組兩個下標的比較,確定兩個子串是否相同 25 inline int cmp(int x,int y,int l){return id[x]==id[y]&&id[x+l]==id[y+l];} 26 int main() { 27 scanf("%s",s+1); 28 n=strlen(s+1); 29 for(int i=1;i<=n;++i) rank[i]=s[i],id[i]=i; 30 m=127,qsort();//一開始是以單個字符為單位,所以(m = 127) 31 for(int l=1,p=1,i;p<n;l<<=1,m=p){ 32 //l 當前一個子串的長度; m 當前離散后的排名種類數 33 //當前的id(第二關鍵字)可直接由上一次的sa的得到 34 //更新sa值,并用id暫時存下上一輪的rank(用于cmp比較) 35 for(p=0,i=n-l+1;i<=n;++i) id[++p]=i;//長度越界,第二關鍵字為0 36 for(i=1;i<=n;++i) if (sa[i]>l) id[++p]=sa[i]-l; 37 qsort(),swap(rank,id),rank[sa[1]]=p=1; 38 //用已經完成的SA來更新與它互逆的rank,并離散rank 39 for(i=2;i<=n;++i) rank[sa[i]]=cmp(sa[i],sa[i-1],l)?p:++p; 40 } 41 //LCP 這個知道原理后就比較好理解程序 42 int j,k=0; 43 for(int i=1;i<=n;height[rank[i++]]=k) 44 for(k=k?k-1:k,j=sa[rank[i]-1];s[i+k]==s[j+k];++k); 45 return 0; 46 }
4個比較基礎的應用
Q1:一個串中兩個串的最大公共前綴是多少??
A1:這不就是Height嗎?用rmq預處理,再O(1)查詢。?
?
Q2:一個串中可重疊的重復最長子串是多長??
A2:就是求任意兩個后綴的最長公共前綴,而任意兩個后綴的最長公共前綴都是Height 數組里某一段的最小值,那最長的就是Height中的最大值。?
?
Q3:一個串種不可重疊的重復最長子串是多長??
A3:先二分答案,轉化成判別式的問題比較好處理。假設當前需要判別長度為k是否符合要求,只需把排序后的后綴分成若干組,其中每組的后綴之間的Height 值都不小于k,再判斷其中有沒有不重復的后綴,具體就是看最大的SA值和最小的SA值相差超不超過k,有一組超過的話k就是合法答案。?
?
A4:一個字符串不相等的子串的個數是多少??
Q4:每個子串一定是某個后綴的前綴,那么原問題等價于求所有后綴之間的不相同的前綴的個數。而且可以發現每一個后綴Suffix[SA[i]]的貢獻是Len - SA[i] + 1,但是有子串算重復,重復的就是Heigh[i]個與前面相同的前綴,那么減去就可以了。最后,一個后綴Suffix[SA[i]]的貢獻就是Len - SA[k] + 1 - Height[k]。?
對于后綴數組更多的應用這里就不詳細闡述,經過思考后每個人都會發現它的一些不同的用途,它的功能也許比你想象中的更強大!
最開始的那道題
先搬下來。。。
你可想想這道題:你有一個01串S,然后定義一個前綴最右邊的位置就是這個前綴的結束位置。現在有很多個詢問,每q個詢問結束位置在l~r中不同前綴的最長公共后綴是多長??
|S|,q≤100000|S|,q≤100000?
時限4s
簡單思路:首先可以把字符串反過來就是求后綴的最長公共前綴了,可以用SA求出height數組,然后用rmq預處理之后就是求兩個位置間的最小值。然后對于一個區間,顯然只有在SA數組中相鄰的兩個串可以貢獻答案。?
對于區間詢問的問題可以用莫隊處理,然后考慮加入一個后綴應該怎么處理,我們可以維護一個按SA數組排序的鏈表。假設我們先把所有位置的SA全部加入,然后按順序刪除,重新按順序加入時就可以O(1)完成修改。那么按照這個思路我們可以用固定左端點的并查集,做到只加入,不刪除,然后用O(nn??√+nlogn)O(nn+nlogn)的復雜度完成這道題。
*可能后面的處理方式比較麻煩,如果直接用splay維護區間中的后綴的話可以做到O(nn??√logn)O(nnlogn),這個方法就比較直觀,而SAM在個問題上還是有點無力的。這題只是為了說明SA相比于SAM還是有他的獨到之處,特別是在處理后綴的lcp之類的問題上。
結束
?






矩陣中的路徑)












