
猴子吃果凍
?
4-EM算法原理及利用EM求解GMM參數過程
1.極大似然估計
原理:假設在一個罐子中放著許多白球和黑球,并假定已經知道兩種球的數目之比為1:3但是不知道那種顏色的球多。如果用放回抽樣方法從罐中取5個球,觀察結果為:黑、白、黑、黑、黑,估計取到黑球的概率為p;
假設p=1/4,則出現題目描述觀察結果的概率為:(1/4)4?*(3/4) = 3/1024
假設p=3/4,則出現題目描述觀察結果的概率為:(3/4)4?*(1/4) = 81/1024
由于81/1024 > 3/1024,因此任務p=3/4比1/4更能出現上述觀察結果,所以p取3/4更為合理
以上便為極大似然估計的原理
定義如下圖:(圖片來自浙江大學概率論課程課件)


2.知曉了極大似然估計的原理之后,我們可以利用極大似然估計的原理來解決如下問題:
即,若給定一圈樣本x1,x2.....xn,已知他們服從高斯分布N(μ,σ),要求估計參數均值μ,標準差σ
(1) 高斯分布的概率密度為:
![]()
(2) 利用上述極大似然估計的原理,構建似然函數為:
![]()
(3) 為例求解方便我們取對數似然:
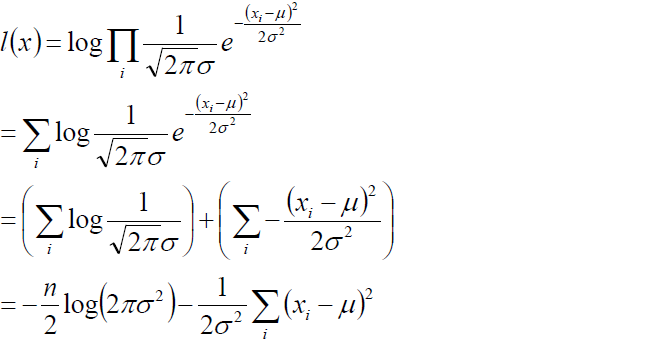
(4) 我們的目標是求上述l(x)的最大值,對上式,分別關于μ,σ求二階導數,很容易證明2次倒數均小于0 ,所以上述函數關于μ,和σ均為凹函數,極大值點滿足一階導數等于0,故通過對μ,和σ求偏導并且倒數為0 我們即可得到如下等式:
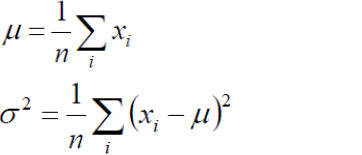
3.EM算法原理推導
3.1 EM算法與極大似然估計的區別于聯系(直接飲用李航-統計學習方法中的內容)
概率模型有時即含有觀測變量,又含有隱變量或潛在變量,如果概率模型的變量都是觀測變量,那么給定數據,可以直接用極大似然估計法,或者貝葉斯估計法估計模型參數。但是當模型含有隱量時,就不能簡單的用這些估計方法,EM算法就是含有隱變量的概率模型參數的極大似然估計法
什么是隱變量?
舉例:比如現要在一所學校中隨機選取1000個人測量身高,最終我們會得到一個包含1000個身高數據的數據集,此數據集就稱為觀測變量,那這1000個學生中,既有男生又有女生,我們在選取完成以后并不知道男生和女生的比例是多少?此時這1000名學生中男生的占比以及女生的占比就稱為隱變量
3.2 有了上述簡單的認識之后,下邊解決EM算法的推導過程
在對EM算法原理進行推導之前,先用一個實例理解一下下文中θ所表示的意義:
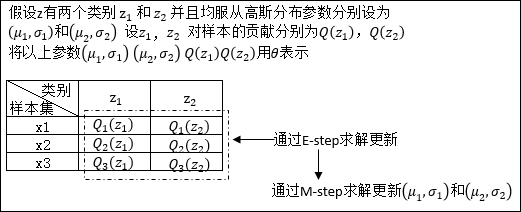
假設現有樣本集T= {x1,x2?.....xm},包含m個獨立樣本,其中每個樣本對應的類別z(這里的類別z就可以類比3.1中的男生女生兩種性別去理解)是未知的,所以很難直接用極大似然法去求解。
以x1為例:x1發生的概率可以表示為:![]() ,θ表示的就是我們要估計的參數的一個總稱后續證明過程中的Q(z)也是θ中的一個參數。舉例,如果每一個類別z均符合高斯分布,那么θ中還會包含均值μ和標準差σ,如果對θ的理解不是不到
,θ表示的就是我們要估計的參數的一個總稱后續證明過程中的Q(z)也是θ中的一個參數。舉例,如果每一個類別z均符合高斯分布,那么θ中還會包含均值μ和標準差σ,如果對θ的理解不是不到
整個數據集T的似然函數可以表示為:
![]()
為了便于計算我們取對數似然得:
![]()
對上上述函數log中有求和運算,求解困難,故我們可以對其形式進行轉化,轉化為易于我們求解的方式如下式: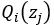 表示第i個樣本第j個類別的概率,則
表示第i個樣本第j個類別的概率,則![]() 表示
表示![]() 的期望
的期望
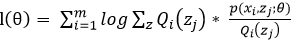
log函數是一個凹函數,故利用jenson不等式的原理可以得出期望的函數值大于等于函數值的期望,故表達如下:

![]() 在上述不等式的等號成立時和
在上述不等式的等號成立時和![]() 是等價的,也就是說后式的最大值即為前式的最大值。當log函數的圖像是一條直線時等號成立,故
是等價的,也就是說后式的最大值即為前式的最大值。當log函數的圖像是一條直線時等號成立,故![]() 為常數時,等號成立。 ? ?
為常數時,等號成立。 ? ?
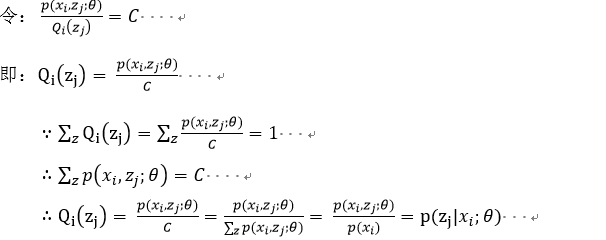
#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#
E-step:即就是上述的![]()
M-step:在E-step的基礎上求使得上述函數值的期望取得最大值的參數θ的取值
?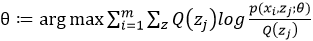
#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#-#
對上述E-step和M-step不斷進行迭代,知道我們估計的模型參數收斂(即變化趨近于一個定值)我們即可得到最適合觀測數據集的模型參數,者便是EM算法
4.利用EM原理推導GMM(混合高斯模型)
隨機變量X是有K個高斯分布混合而成,取各個高斯分布的概率為φ1,φ2...φK,第i個高斯分布的均值為μi,方差為Σi。若觀測到隨機變量X的一系列樣本x1,x2...xn,試估計參數φ,μ,Σ。? ??
? 第一步:依據3中E-step估計φ用wj(i)?表示,意義是對第i個樣本第j個高斯分布的貢獻率(即第j個高斯分布的占比)
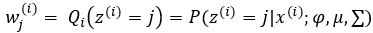
第二步:依據3中的M-step估計μ,和σ ?用? 表示σ2
表示σ2
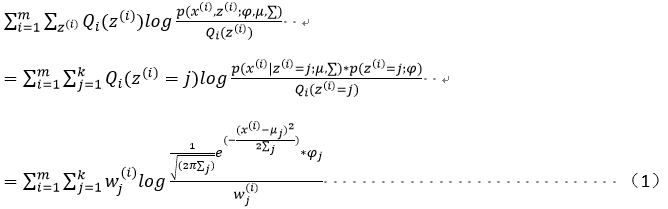
對上述關于μ求偏導得:

對(2)式為0 可得:
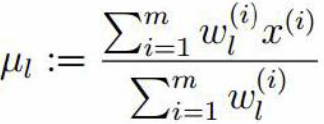
同理對方差求偏導,并令導入為0 可得:
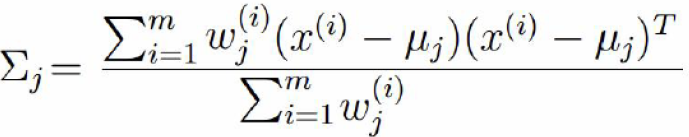
對于φj?由于?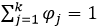 ,故對于φj?必須采用添加極值的方式求解,需構建拉個朗日方程進行求解。
,故對于φj?必須采用添加極值的方式求解,需構建拉個朗日方程進行求解。
觀察(1)式,log函數中可以看成是一個常數與φj相乘。由對數函數求導法則指,在求導之后,常數項終被抵消,如f(x) = lnax 關于x求導結果與g(x)=lnx關于x求導結果相同,故對于(1)式在構建拉個朗日函數時,直接去掉log函數中的常數項,如下:
由于φj?為正在log函數中已有現值,故這里無需構建不等式約束
![]()
對朗格朗日函數關于φj求導并取倒數為0 可得:
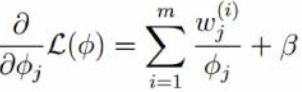
![]()
![]()
5.用實例理解GMM的參數估計過程
5.1 在正式引入GMM(混合高斯模型)前我們以下述情景的求解為例,用實例看先熟悉以下參數更新的過程
情景:假設從商場隨機選取10位顧客,測量這10位顧客的身高,這些顧客中既包含男性顧客也包含女性顧客,現在我們已知測量數據,T=[x1,x2.....x10]為我們測試的身高數據,即為可觀測數據集。并且知道男性女性顧客的身高均服從高斯分布N(μ1,σ1),N(μ2,σ2),估計參數μ1,σ1,μ2,σ2?,以及男女比例?α1,α2;
高斯分布的概率密度函數為:
![]()
(1)對于測試數據x1?其產生的概率我們可以表示為:
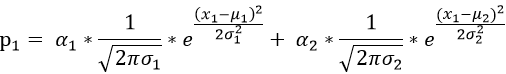
我們用γ(i,k)來表示男性或者女性在生成數據x1??時所做的貢獻(γ(i,k)就相當于我們初始給定的α1,α2)。或者說表示單由男性或者女性產生數據xi的概率,前后兩個說法所想表達的意思是相同的,那么就有:
?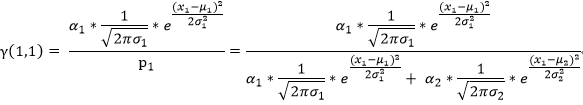
?
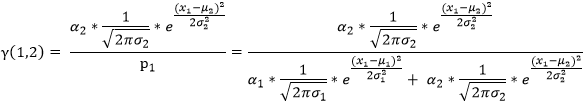
?
(2)對于測試數據x2?其產生的概率我們可以表示為:
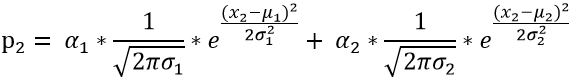
同(1)可知:
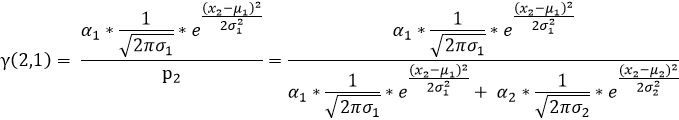
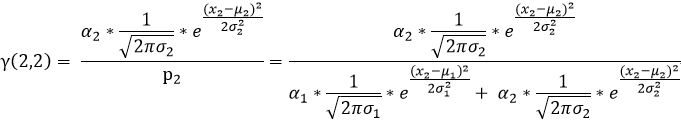
(3)依次按照上述(1)(2)的規律我們就可以求出如下表格中的所有值,表中標綠的在上述(1)(2)步已求出
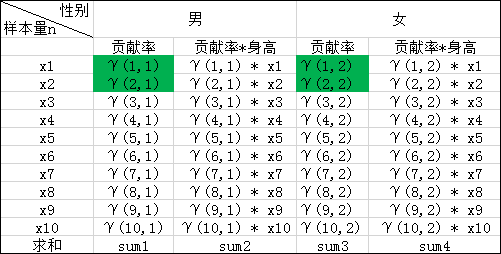
我們在上文2中的(4)已經推導出來了μ和σ2的計算公式,故
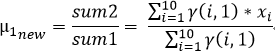 ? ?
? ?
? ?
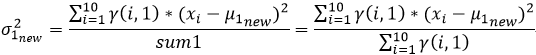

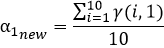 ?
?
? ?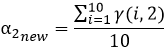
對于上述α1,α2計算方式的理解:α1,α2表示的是同一次實驗,或者說針對同一個樣本,兩類數據來源(男性,女性)對樣本結果的貢獻率,那么對于每一個樣本來說他們的男性和女性的貢獻率都應該是恒定的,故我們采用取平均的方式更新α1,α2;
(4)用計算出來的μ1new,μ2new ? ? ?σ21new ???σ22new ??α1new,α2new?再次重復迭代上述(1)(2)(3)步驟,直到μ1new,μ2new ? ? ?σ21new ???σ22new ??α1new,α2new?收斂我們即得到的關于本次觀測數據最合適的參數
5.2 有了上述實例以后,我們直接給出GMM的推廣式:(下述式子的正面過程見4中GMM的證明過程)
隨機變量X是有K個高斯分布混合而成,取各個高斯分布的概率為φ1,φ2...φK,第i個高斯分布的均值為μi,方差為Σi。若觀測到隨機變量X的一系列樣本x1,x2...xn,試估計參數φ,μ,Σ。
第一步:(如上述實例中(1)和(2))

第二步:(如上述實例中的(3))
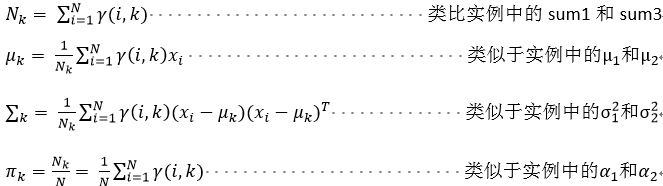
?

















)


)