Canny邊緣檢測

聲明：閱讀本文需要了解線性代數里面的點乘（圖像卷積的原理），高等數學里的二元函數的梯度，極大值定義，了解概率論里的二維高斯分布

1.canny邊緣檢測原理和簡介

2.實現步驟

3.總結

一、 Canny邊緣檢測算法的發展歷史

　　Canny算子是28歲的John?Canny在1986年提出的，該文章發表在PAMI頂級期刊(1986.?A computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 8, 1986, pp. 679-698)。現在老大爺目前（61歲）在加州伯克利做machine learning,主頁(http://www.cs.berkeley.edu/~jfc/)，大爺就是大爺。

　　邊緣檢測是從圖像中提取有用的結構信息的一種技術，如果學過信息論就會知道，一面充滿花紋的墻要比一面白墻的信息量大很多，沒學過也沒關系，直觀上也能理解：充滿花紋的圖像要比單色圖像信息更豐富。為什么要檢測邊緣?因為我們需要計算機自動的提取圖像的底層（紋理等）或者高層（時間地點人物等）的信息，邊緣可以說是最直觀、最容易發現的一種信息了。Canny提出了一個對于邊緣檢測算法的評價標準，包括：

1)??????? 以低的錯誤率檢測邊緣，也即意味著需要盡可能準確的捕獲圖像中盡可能多的邊緣。

2)??????? 檢測到的邊緣應精確定位在真實邊緣的中心。

3)??????? 圖像中給定的邊緣應只被標記一次，并且在可能的情況下，圖像的噪聲不應產生假的邊緣。

　　簡單來說就是，檢測算法要做到：邊緣要全，位置要準，抵抗噪聲的能力要強。?

　　接下來介紹最經典的canny邊緣檢測算法，很多邊緣檢測算法都是在此基礎上進行改進的，學習它有利于一通百通。

二、實現步驟

　　step1：高斯平滑濾波

沒有哪張圖片是沒有噪聲的。————魯迅

　　濾波是為了去除噪聲，選用高斯濾波也是因為在眾多噪聲濾波器中，高斯表現最好（表現怎么定義的？最好好到什么程度？），你也可以試試其他濾波器如均值濾波、中值濾波等等。一個大小為(2k+1)x(2k+1)的高斯濾波器核（核一般都是奇數尺寸的）的生成方程式由下式給出：

? ?‘

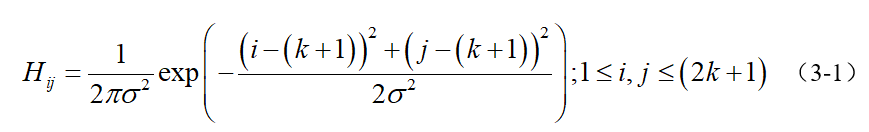　　下面是一個sigma = 1.4，尺寸為3x3的高斯卷積核的例子，注意矩陣求和值為1（歸一化）：

　　舉個例子：若圖像中一個3x3的窗口為A，要濾波的像素點為e，則經過高斯濾波之后，像素點e的亮度值為：

?　　其中*為卷積符號，sum表示矩陣中所有元素相加求和，簡單說，就是濾波后的每個像素值=其原像素中心值及其相鄰像素的加權求和。圖像卷積是圖像處理中非常重要且廣泛使用的操作，一定要理解好。

其中高斯卷積核的大小將影響Canny檢測器的性能。尺寸越大，去噪能力越強，因此噪聲越少，但圖片越模糊，canny檢測算法抗噪聲能力越強，但模糊的副作用也會導致定位精度不高，一般情況下，推薦尺寸5*5，3*3也行。

　　step2：?計算梯度強度和方向

邊緣的最重要的特征是灰度值劇烈變化，如果把灰度值看成二元函數值，那么灰度值的變化可以用二元函數的”導數“（或者稱為梯度）來描述。由于圖像是離散數據，導數可以用差分值來表示，差分在實際工程中就是灰度差，說人話就是兩個像素的差值。一個像素點有8鄰域，那么分上下左右斜對角，因此Canny算法使用四個算子來檢測圖像中的水平、垂直和對角邊緣。算子是以圖像卷積的形式來計算梯度，比如Roberts，Prewitt，Sobel等，這里選用Sobel算子來計算二維圖像在x軸和y軸的差分值（這些數字的由來？），將下面兩個模板與原圖進行卷積，得出x和y軸的差分值圖，最后計算該點的梯度G和方向θ

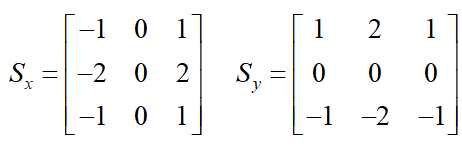
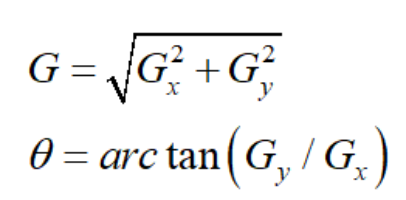
　　計算梯度的模和方向屬于高等數學部分的內容，如果不理解應該補習一下數學基本功，圖像處理經常會用到這個概念。

　　這部分我實現了下，首先了解opencv的二維濾波函數：dst=cv.filter2D(src, ddepth, kernel[, dst[, anchor[, delta[, borderType]]]])?

　　dst：　　輸出圖片

　　src：　　輸入圖片

　　ddepth：輸出圖片的深度, 詳見?combinations,如果填-1，那么就跟與輸入圖片的格式相同。

　　kernel：? ?單通道、浮點精度的卷積核。

　　以下是默認參數：

　　anchor：內核的基準點(anchor)，其默認值為(-1,-1)表示位于kernel的中心位置。基準點即kernel中與進行處理的像素點重合的點。舉個例子就是在上面的step1中，e=H*A得到的e是放在原像素的3*3的哪一個位置，一般來說都是放在中間位置，設置成默認值就好。

　　delta ：在儲存目標圖像前可選的添加到像素的值，默認值為0。（沒用過）

　　borderType：像素向外逼近的方法，默認值是BORDER_DEFAULT,即對全部邊界進行計算。（沒用過）

　　上代碼

 1 import cv2
 2 import numpy as np
 3 import matplotlib.pyplot as plt
 4 
 5 
 6 img=cv2.imread("images/luxun.png",cv2.IMREAD_GRAYSCALE)  # 讀入圖片
 7 sobel_x = np.array([[-1, 0, 1],[-2,0,+2],[-1, 0, 1]])    # sobel的x方向算子
 8 sobel_y = np.array([[1, 2, 1],[0,0,0],[-1, -2, -1]])     # sobel的x方向算子
 9 sobel_x=cv2.flip(sobel_x,-1)          # cv2.filter2D()計算的是相關，真正的卷積需要翻轉，在進行相關計算。
10 sobel_x=cv2.flip(sobel_y,-1)
11 # cv2.flip()第二個參數：等于0：沿著x軸反轉。大于0：沿著y軸反轉。小于零：沿著x軸，y軸同時反轉
12 
13 # 卷積 opencv是用濾波器函數實現的
14 img_x=cv2.filter2D(img,-1, sobel_x)
15 img_y=cv2.filter2D(img,-1, sobel_y)
16 # 畫圖 plt不支持中文，但是可以通過以下方法設置修復
17 plt.rcParams['font.sans-serif']=['SimHei']
18 plt.rcParams['axes.unicode_minus'] = False
19 
20 plt.subplot(221), plt.imshow(img_x, 'gray'),plt.title('sobel_x')
21 plt.subplot(222), plt.imshow(img_y, 'gray'),plt.title('sobel_y')
22 plt.subplot(223), plt.imshow(img_y+img_x, 'gray'),plt.title('sobel')
23 plt.subplot(224), plt.imshow(img, 'gray'),plt.title('原圖')
24 plt.show()

View Code

　　運行效果：

　　　　需要注意一點：在圖像處理領域，卷積運算的定義是先將核關于x軸和y軸反轉，然在做相關運算。然而工程實踐中往往跳過反轉，用相關運算代替卷積（比如opencv）。如果你需要嚴格的卷積運算，應該注意原函數的具體實現方式。sobel算子天生關于中心對稱，所以反轉與否并不影響結果（我在代碼里用cv2.flip（）進行了反轉操作）。

　　　　在之后的實現中，我發現用opencv自帶的濾波函數算出來的梯度是歸一化到（0-255）的，引入其他的庫也很麻煩，因此自己寫了個簡單的二位卷積函數來實現梯度計算。所以上面的圖適合看效果，并不適合在程序中使用，卷積函數的代碼如下：

 1 def conv2d(src,kernel):  # 輸入必須為方形卷積核
 2     # 本函數仍然是相關運算，沒有反轉。如果非要嚴格的卷積運算，把下面一行代碼的注釋取消。
 3     #kernel=cv2.flip(kernel,-1)
 4     [rows,cols] = kernel.shape
 5     border=rows//2                                  # 向下取整 獲得卷積核邊長
 6     [rows,cols]=src.shape
 7     dst = np.zeros(src.shape)                       # 采用零填充再卷積，卷積結果不會變小。
 8     # print("圖像長：",rows,"寬：",cols,"核邊界",border)
 9     # print(border,rows-border,border,cols-border)
10     temp=[]
11     for i in range(border,rows-border):
12         for j in range(border,cols-border):
13             temp=src[i-border:i+border+1,j-border:j+border+1]  # 從圖像獲取與核匹配的圖像
14             # 切片語法：索引位置包括開頭但不包括結尾 [start: end: step]
15             dst[i][j]=(kernel*temp).sum()  # 計算卷積
16     return dst

View Code

?　　　　小技巧：用plt顯示二維矩陣，鼠標移到某個像素就會顯示坐標（x，y）和灰度值，浮點數也可以顯示。這可以很方便的看某個數據（像素點）是否有問題。

　　　　梯度和幅值的計算效果如下：

?　　　　　　能看出來sobel算子計算的邊緣很粗很亮，比較明顯，但是不夠精確，我們的目標是精確到一個像素寬，至于梯度相位就很難看出什么特征，并且梯度相位實際上是為了下一步打基礎的。下面附上代碼：

1 img_x=conv2d(img,sobel_x)  # 使用我自己的寫的卷積計算梯度
2 img_y=conv2d(img,sobel_y)
3 G=np.sqrt(img_x*img_x+img_y*img_y)  # 梯度幅值
4 theta=np.arctan(img_y,(img_x+0.0000000000001))*180/np.pi  # 化為角度，分母+極小值是為了避免除以0
5 # plt.imshow(theta, 'gray'),plt.title('梯度相位')
6 plt.imshow(G, 'gray'),plt.title('梯度幅值')
7 plt.show()

View Code

　　step3:非極大值抑制

　　　　　　sobel算子檢測出來的邊緣太粗了，我們需要抑制那些梯度不夠大的像素點，只保留最大的梯度，從而達到瘦邊的目的。這些梯度不夠大的像素點很可能是某一條邊緣的過渡點。按照高數上二位函數的極大值的定義，即對點（x0，y0）的某個鄰域內所有（x，y）都有f（x，y）≤(f（x0，y0），則稱f在（x0，y0）具有一個極大值，極大值為f（x0，y0）。簡單方案是判斷一個像素點的8鄰域與中心像素誰更大，但這很容易篩選出噪聲，因此我們需要用梯度和梯度方向來輔助確定。

　　　　　　如下圖所示，中心像素C的梯度方向是藍色直線，那么只需比較中心點C與dTmp1和dTmp2的大小即可。由于這兩個點的像素不知道，假設像素變化是連續的，就可以用g1、g2和g3、g4進行線性插值估計。設g1的幅值M(g1)，g2的幅值M(g2),則M(dtmp1)=w*M(g2)+(1-w)*M(g1)? ，其w=distance(dtmp1,g2)/distance(g1,g2)? 。也就是利用g1和g2到dTmp1的距離作為權重，來估計dTmp1的值。w在程序中可以表示為tan（θ）來表示，具體又分為四種情況（下面右圖）討論。

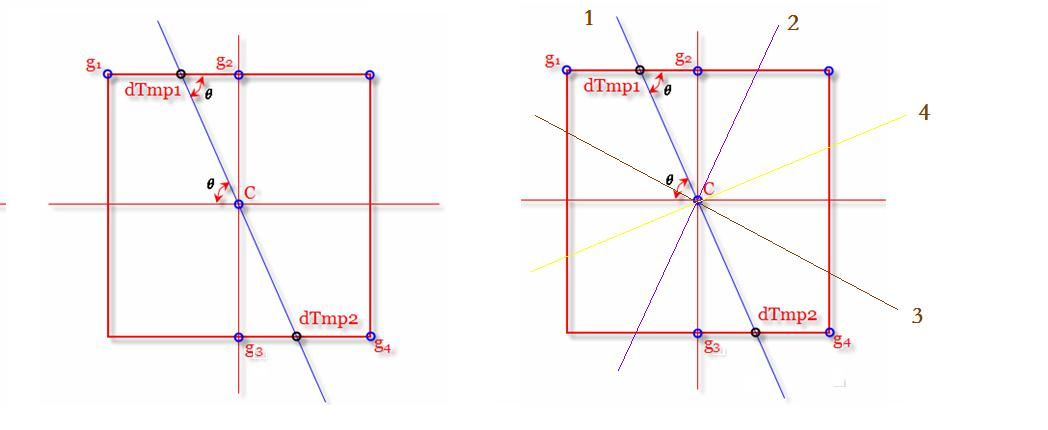
　　　　　　如下圖，經過非極大值抑制可以很明顯的看出去除了很多點，邊緣也變得很細。在程序實現中，要注意opencv的默認坐標系是從左到右為x軸，從上到下是y軸，原點位于左上方，計算g1、g2、g3、g4的位置的時候，一定要小心（坑了我很久）。經過非極大值抑制可以看出來圖片的邊緣明顯變細，很多看起來黑色的部分其實有值的，只是因為值太小了看不清楚，而這些黑色的部分可能是噪聲或者其他原因造成的局部極大值，下一步我們就要用雙閾值來限定出強邊緣和弱邊緣，盡可能的減少噪聲的檢出。代碼附上：

 1 # step3:非極大值抑制
 2 anchor=np.where(G!=0)  # 獲取非零梯度的位置
 3 Mask=np.zeros(img.shape)
 4 
 5 for i in range(len(anchor[0])):
 6     x=anchor[0][i]
 7     y=anchor[1][i]
 8     center_point=G[x,y]
 9     current_theta=theta[x,y]
10     dTmp1=0
11     dTmp2=0
12     W=0
13     if current_theta>=0 and current_theta<45:
14         #        g1         第一種情況
15         # g4  C  g2
16         # g3
17         g1 = G[x + 1, y - 1]
18         g2 = G[x + 1, y]
19         g3 = G[x - 1, y + 1]
20         g4 = G[x - 1, y]
21         W=abs(np.tan(current_theta*np.pi/180))  # tan0-45范圍為0-1
22         dTmp1= W*g1+(1-W)*g2
23         dTmp2= W*g3+(1-W)*g4
24 
25     elif current_theta>=45 and current_theta<90:
26         #     g2 g1         第二種情況
27         #     C
28         # g3  g4
29 
30         g1 = G[x + 1, y - 1]
31         g2 = G[x, y - 1]
32         g3 = G[x - 1, y + 1]
33         g4 = G[x, y + 1]
34         W = abs(np.tan((current_theta-90) * np.pi / 180))
35         dTmp1= W*g1+(1-W)*g2
36         dTmp2= W*g3+(1-W)*g4
37 
38     elif current_theta>=-90 and current_theta<-45:
39         # g1  g2            第三種情況
40         #     C
41         #     g4 g3
42         g1 = G[x - 1, y - 1]
43         g2 = G[x, y - 1]
44         g3 = G[x + 1, y + 1]
45         g4 = G[x, y + 1]
46         W = abs(np.tan((current_theta-90) * np.pi / 180))
47         dTmp1= W*g1+(1-W)*g2
48         dTmp2= W*g3+(1-W)*g4
49 
50     elif current_theta>=-45 and current_theta<0:
51         # g3                第四種情況
52         # g4  C  g2
53         #        g1
54         g1 = G[x + 1, y + 1]
55         g2 = G[x + 1, y]
56         g3 = G[x - 1, y - 1]
57         g4 = G[x - 1, y]
58         W = abs(np.tan(current_theta * np.pi / 180))
59         dTmp1= W*g1+(1-W)*g2
60         dTmp2= W*g3+(1-W)*g4
61 
62     if dTmp1<center_point and dTmp2<center_point:   # 記錄極大值結果
63             Mask[x,y]=center_point
64 #Mask=(Mask-Mask.min())/(Mask.max()-Mask.min())*256 #歸一化
65 plt.imshow(Mask,'gray'),plt.title('Mask')
66 plt.show()

View Code

　　step4：用雙閾值算法檢測和連接邊緣

?　　　　　　雙閾值法非常簡單，我們假設兩類邊緣：經過非極大值抑制之后的邊緣點中，梯度值超過T1的稱為強邊緣，梯度值小于T1大于T2的稱為弱邊緣，梯度小于T2的不是邊緣。可以肯定的是，強邊緣必然是邊緣點，因此必須將T1設置的足夠高，以要求像素點的梯度值足夠大（變化足夠劇烈），而弱邊緣可能是邊緣，也可能是噪聲，如何判斷呢？當弱邊緣的周圍8鄰域有強邊緣點存在時，就將該弱邊緣點變成強邊緣點，以此來實現對強邊緣的補充。實際中人們發現T1:T2=2:1的比例效果比較好，其中T1可以人為指定，也可以設計算法來自適應的指定，比如定義梯度直方圖的前30%的分界線為T1，我實現的是人為指定閾值。檢查8鄰域的方法叫邊緣滯后跟蹤，連接邊緣的辦法還有區域生長法等等。強邊緣、弱邊緣、綜合效果、和opencv的canny函數對比如下：

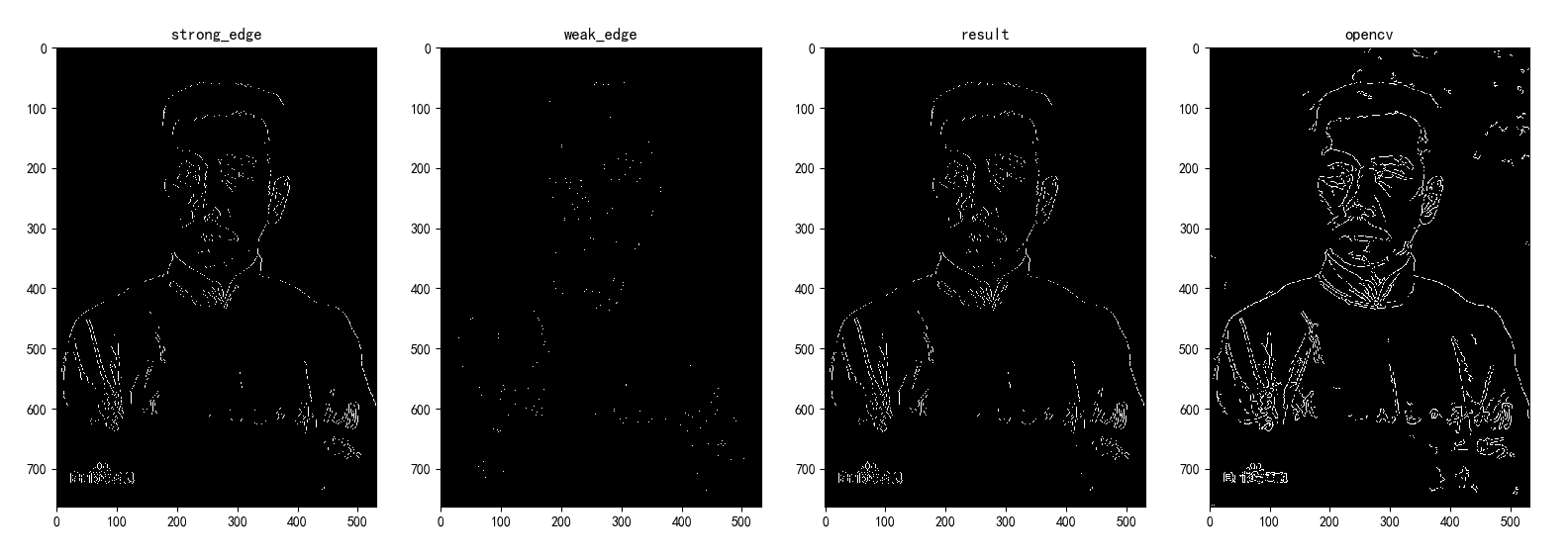
三、總結

　　　　實現結果還是很打擊的，我檢測到的邊緣過于斷續，沒有opencv實現的效果好。查了一下opencv的源碼，這里猜測兩個可能的原因：源碼里梯度的方向被近似到四個角度之一（0，45，90，135），但我用線性插值的的結果是梯度方向更精確，而過于精確-->過于嚴格-->容易受到噪聲干擾，所以在非極大值抑制這之后，我比opencv少了更多的點，最終導致了邊緣不夠連續；第二個原因可能是邊緣連接算法效果不夠好，把圖象放大來看，我產生的邊緣傾向于對角線上連接，而opencv的邊緣傾向于折線連接，因此opencv的邊緣更完整連續，而我的邊緣更細，更容易斷續。

　　　　限于時間，暫時研究到這里，希望各位多多指正！感謝所有我參考過的博客和文檔！

  1 import cv2
  2 import numpy as np
  3 import matplotlib.pyplot as plt
  4 
  5 # 畫圖 plt不支持中文，但是可以通過以下方法設置修復
  6 plt.rcParams['font.sans-serif']=['SimHei']
  7 plt.rcParams['axes.unicode_minus'] = False
  8 
  9 def conv2d(src,kernel):  # 輸入必須為方形卷積核
 10     # 本函數仍然是相關運算，沒有反轉。如果非要嚴格的卷積運算，把下面一行代碼的注釋取消。
 11     #kernel=cv2.flip(kernel,-1)
 12     [rows,cols] = kernel.shape
 13     border=rows//2                                  # 向下取整 獲得卷積核邊長
 14     [rows,cols]=src.shape
 15     dst = np.zeros(src.shape)                       # 采用零填充再卷積，卷積結果不會變小。
 16     # print("圖像長：",rows,"寬：",cols,"核邊界",border)
 17     # print(border,rows-border,border,cols-border)
 18     temp=[]
 19     for i in range(border,rows-border):
 20         for j in range(border,cols-border):
 21             temp=src[i-border:i+border+1,j-border:j+border+1]  # 從圖像獲取與核匹配的圖像
 22             # 切片語法：索引位置包括開頭但不包括結尾 [start: end: step]
 23             dst[i][j]=(kernel*temp).sum()  # 計算卷積
 24     return dst
 25 
 26 
 27 # step0:讀入圖片
 28 img=cv2.imread("images/luxun.png",cv2.IMREAD_GRAYSCALE)  # 讀入圖片
 29 
 30 # step1:高斯濾波
 31 img=cv2.GaussianBlur(img,(5,5),0)
 32 
 33 # step2:計算梯度強度和方向
 34 sobel_x = np.array([[-1, 0, 1],[-2,0,+2],[-1, 0, 1]])   # sobel的x方向算子
 35 sobel_y = np.array([[1, 2, 1],[0,0,0],[-1, -2, -1]])    # sobel的y方向算子
 36 
 37 # img_x=cv2.filter2D(img,-1, sobel_x)  # 這個濾波器會將卷積結果歸一化到0-255，無法計算梯度方向。
 38 # img_y=cv2.filter2D(img,-1, sobel_y)  # 而真正的圖像卷積可能會出現負數，因此只能自己寫個卷積。
 39 img_x=conv2d(img,sobel_x)  # 使用我自己的寫的卷積計算梯度
 40 img_y=conv2d(img,sobel_y)
 41 G=np.sqrt(img_x*img_x+img_y*img_y)  # 梯度幅值
 42 theta=np.arctan(img_y,(img_x+0.0000000000001))*180/np.pi  # 化為角度，分母+極小值是為了避免除以0
 43 
 44 # plt.imshow(theta, 'gray'),plt.title('梯度相位')
 45 # plt.imshow(G, 'gray'),plt.title('梯度幅值')
 46 # plt.show()
 47 # exit()
 48 
 49 # step3:非極大值抑制
 50 anchor=np.where(G!=0)  # 獲取非零梯度的位置
 51 Mask=np.zeros(img.shape)
 52 for i in range(len(anchor[0])):
 53     x=anchor[0][i]  # 取出第i個非零梯度的x坐標
 54     y=anchor[1][i]
 55     center_point=G[x,y]
 56     current_theta=theta[x,y]
 57     dTmp1=0
 58     dTmp2=0
 59     W=0
 60     if current_theta>=0 and current_theta<45:
 61         #        g1         第一種情況
 62         # g4  C  g2
 63         # g3
 64         g1 = G[x + 1, y - 1]
 65         g2 = G[x + 1, y]
 66         g3 = G[x - 1, y + 1]
 67         g4 = G[x - 1, y]
 68         W=abs(np.tan(current_theta*np.pi/180))  # tan0-45范圍為0-1
 69         dTmp1= W*g1+(1-W)*g2
 70         dTmp2= W*g3+(1-W)*g4
 71 
 72     elif current_theta>=45 and current_theta<90:
 73         #     g2 g1         第二種情況
 74         #     C
 75         # g3  g4
 76         g1 = G[x + 1, y - 1]
 77         g2 = G[x, y - 1]
 78         g3 = G[x - 1, y + 1]
 79         g4 = G[x, y + 1]
 80         W = abs(np.tan((current_theta-90) * np.pi / 180))
 81         dTmp1= W*g1+(1-W)*g2
 82         dTmp2= W*g3+(1-W)*g4
 83     elif current_theta>=-90 and current_theta<-45:
 84         # g1  g2            第三種情況
 85         #     C
 86         #     g4 g3
 87         g1 = G[x - 1, y - 1]
 88         g2 = G[x, y - 1]
 89         g3 = G[x + 1, y + 1]
 90         g4 = G[x, y + 1]
 91         W = abs(np.tan((current_theta-90) * np.pi / 180))
 92         dTmp1= W*g1+(1-W)*g2
 93         dTmp2= W*g3+(1-W)*g4
 94     elif current_theta>=-45 and current_theta<0:
 95         # g3                第四種情況
 96         # g4  C  g2
 97         #        g1
 98         g1 = G[x + 1, y + 1]
 99         g2 = G[x + 1, y]
100         g3 = G[x - 1, y - 1]
101         g4 = G[x - 1, y]
102         W = abs(np.tan(current_theta * np.pi / 180))
103         dTmp1= W*g1+(1-W)*g2
104         dTmp2= W*g3+(1-W)*g4
105 
106     if dTmp1<center_point and dTmp2<center_point:   # 記錄極大值結果
107             Mask[x,y]=center_point
108 # plt.imshow(Mask,'gray'),plt.title('Mask')
109 # plt.show()
110 # exit()
111 
112 # step4:雙閾值選取
113 high_threshold=100
114 low_threshold=high_threshold/2
115 strong_edge=np.zeros(G.shape)   # 強邊緣
116 weak_edge=np.zeros(G.shape)     # 弱邊緣
117 
118 xNum = [1, 1, 0, -1, -1, -1, 0, 1]  # 8鄰域偏移坐標
119 yNum = [0, 1, 1, 1, 0, -1, -1, -1]
120 [rows, cols] = G.shape
121 for i in range(rows):
122     for j in range(cols):
123         current_point=Mask[i,j]    
124         if current_point>0:
125             if current_point>high_threshold:   # 強邊緣提取
126                 strong_edge[i,j]=255
127             elif current_point<high_threshold and current_point>low_threshold:  # 弱邊緣提取
128                 # step6:順便進行邊緣連接
129                 change = True
130                 while change:
131                     change = False
132                     for k in range(8):
133                         xx=i+xNum[k]
134                         yy=j+yNum[k]
135                         if Mask[xx,yy]>high_threshold:
136                             weak_edge[i, j] = 255
137                             break  # 跳出八鄰域循環
138 output=strong_edge+weak_edge    # 強弱邊緣綜合效果
139 
140 img_edge = cv2.Canny(img, 50, 100)  # opencv實現效果
141 
142 # 顯示效果
143 plt.subplot(141), plt.imshow(strong_edge, 'gray'),plt.title('strong_edge')
144 plt.subplot(142), plt.imshow(weak_edge, 'gray'),plt.title('weak_edge')
145 plt.subplot(143), plt.imshow(output, 'gray'),plt.title('result')
146 plt.subplot(144), plt.imshow(img_edge, 'gray'),plt.title('opencv')
147 plt.show()