優化器，SGD+Momentum；Adagrad；RMSProp；Adam

Optimization

?

隨機梯度下降（SGD）：

當損失函數在一個方向很敏感在另一個方向不敏感時，會產生上面的問題，紅色的點以“Z”字形梯度下降，而不是以最短距離下降；這種情況在高維空間更加普遍。

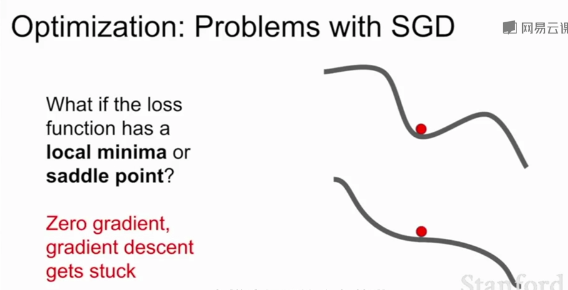
SGD的另一個問題：損失函數容易卡在局部最優或鞍點（梯度為0）不再更新。在高維空間鞍點更加普遍

?

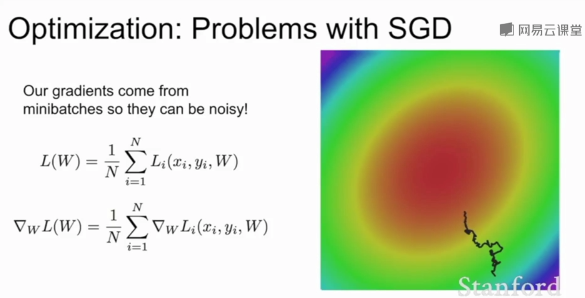
當模型較大時SGD耗費龐大計算量，添加隨機均勻噪聲時SGD需要花費大量的時間才能找到極小值。

?

SGD+Momentum：

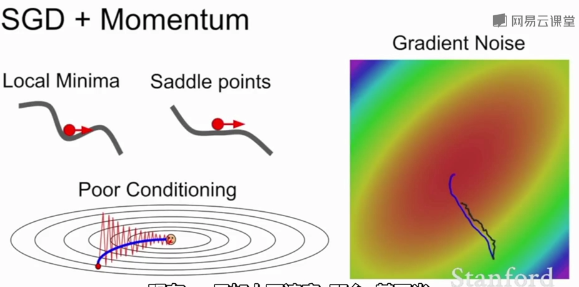
帶動量的SGD，基本思想是：保持一個不隨時間變化的速度，并將梯度估計添加到這個速度上，在這個速度方向上前進，而不是隨梯度變化方向，給一個摩擦系數作為這個速度的衰減項。

?

這種方法解決了局部極小值和鞍點問題，盡管在局部極小值和鞍點任會有朝預定速度方向步進，且速度會隨著時間的速度增加。

?

普通的Momentum更新是先估計當前梯度向量，取其和速度向量的和的方向作為真實參數更新的方向

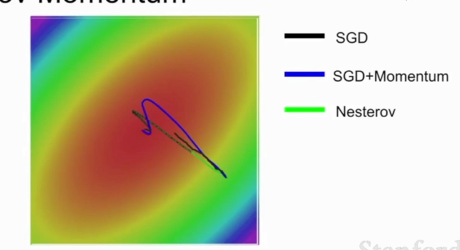
Nesterov Momentum則相反，先取得速度方向的步進，再估計當前位置的梯度，隨后回到原來位置，再根據兩者的和作為真實參數更新的方向。在凸優化問題有良好表現

?Nesterov Momentum不會劇烈的越過局部最小值

?

?

?AdaGrad：

?在優化過程中，需要保持一個在訓練過程中的每一步的梯度的平方和的持續估計；與速度項不同，梯度平方項在訓練時，會一直累加當前梯度的平方到這個梯度平方項，在更新參數向量時，會除以這個梯度平方項。

?

?當一個維度上的梯度更新很小時會除以很小的平方項，梯度很大時則會除以很大的平方項；在一個維度上（梯度下降很慢的）訓練會加快，在另一個維度方向上訓練減慢；讓各個參數得到相同程度的收斂。

隨著時間的推移，梯度更新的步長會越來越小（梯度平方項隨時間單調遞增）；在學習目標是一個凸函數的情況下，效果很好，到達極值點，步長越來越小最終收斂；非凸函數則會變得復雜

?

?

?RMSProp：

?不僅加上平方項，并讓平方梯度按照一定比率下降，然后用1減去衰減了乘以梯度平方加上之前的結果。

隨著訓練的進行，步長會有一個良好的性質，與AdaGrad類似在一個維度上（梯度下降很慢的）訓練會加快，在另一個維度方向上訓練減慢，RMSProp讓梯度平方衰減了，可能會造成訓練一直在變慢。

?

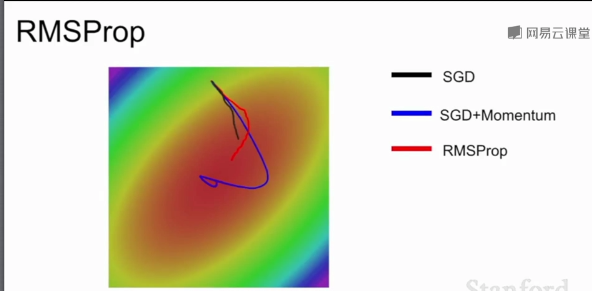
?RMSProp會慢慢調整梯度更新方向，SGD效果不好，SGD+Momentum會先繞過極小值再朝極小值方向前進，AdaGrad在較小學習率時可能會卡住。（凸優化問題）

?

?

?Adam：

更新第一動量（類似SGD+Momentum中的速度）和第二動量（類似AdaGrad、RMSProp中的梯度的平方項）的估計值，第一動量的估計值等于梯度的加權和，第二動量的動態估計值是梯度平方的動態估計值，相當于速度項與梯度平方項的結合。

?

?在最初的第一步，第二動量的初始值為0，第一步之后衰減值beta2=0.9或0.99，第二動量還是接近于0，除以第二動量后會得到很大的步長，可能導致初始化到一個難以收斂的區域。1e-7為的是分母不為0。

?因此，Adam增加了一個偏置校正項避免出現開始時得到很大步長。

?

?一般網絡的都會使用Adam算法作為優化算法，它結合了SGD和RMSProp的優點。

?

?學習率的選擇：

?一般選擇學習率衰減策略，在訓練的開始選擇較大的學習率，然后隨著步長衰減或指數衰減。

?

?SGD+Momentum的學習率衰減很常見，Adam一般不使用學習率衰減，學習率衰減相當于二階超參數，在開始時不使用，在訓練達到一定瓶頸時再考慮使用。

?

?一階優化與二階優化：

?

?

?

L-BFGS是一個二階優化器

?

?Adam是大多數情況下的默認選擇，如果能承受整個批次的更新且沒有很多隨機性（如風格遷移），可以考慮L-BFGS

?

模型集成是提高測試集準確率的有效辦法，通常選擇一批不同的隨機初始值上訓練N個模型，測試時平均N個模型的結果，能夠緩解過擬合。

?

?

Q1：隨機梯度下降的隨機指得是什么？

Q2：嘗試解釋為什么Adam通常會是一個更好的選擇？（可以結合Momentum和RMSProb的優點解釋）

?

1.隨機梯度下降指的是從批量樣本中隨機選取一個樣本，按照該樣本梯度下降的方向進行梯度下降，
2.Adam的優點：可以解決局部最優和鞍點問題，且下降速度較快，平衡各特征梯度的大小

?

https://blog.csdn.net/weixin_40170902/article/details/80092628