---

一、選擇排序

思想：
將數組第一個元素作為min，然后進行遍歷與其他元素對比，找到比min小的數就進行交換，直到最后一個元素就停止，然后再將第二個元素min，再遍歷，以此下去直到最后一個數據
流程圖：

代碼實現：

//交換
void Swap(int* a,int* b) {int t = *a;*a = *b;*b = t;
}
//打印
void Print(int* arr, int n) {for (int i = 0;i < n; i++)printf("%d ", arr[i]);
}
//直接選擇排序
void SelectSort(int* arr, int size) {for (int i = 0; i < size; i++){int min = i;//從第一個開始//每次從i+1的位置開始就不會影響到前面的了for (int j = i+1; j < size; j++) {//比較if (arr[min] > arr[j])min =j;//記錄下標}Swap(&arr[i], &arr[min]);//交換}}
int main() {int arr[] = { 4，3，1，5，2};
SelectSort(arr, sizeof(arr) / sizeof(arr[0]));
Print(arr, sizeof(arr) / sizeof(arr[0]));return 0;
}

運行結果：

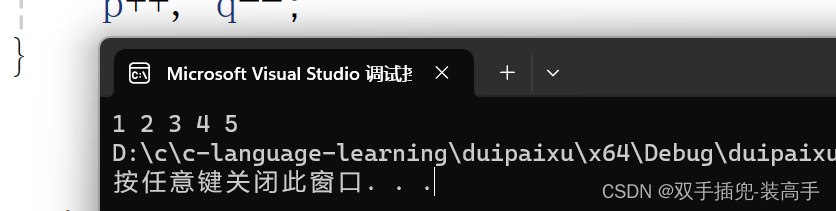
選擇排序優化：
我們可以設置一個min和一個max，將小的放到左邊，大的放到右邊，我們再設置兩個控制左右兩邊下標的變量p，q，當它們相遇時就結束。
流程圖：

特殊情況：max的位置等于p時，我們先交換arr[p]和arr[min],但是max指向p這個位置，但是p這位置的值已經改變了，這時我們就要進行糾正，將max=min，這樣才能成功找到原來在p位置的值
如：

代碼實現：

//交換
void Swap(int* a,int* b) {int t = *a;*a = *b;*b = t;
}
//打印
void Print(int* arr, int n) {for (int i = 0;i < n; i++)printf("%d ", arr[i]);
}
//優化選擇排序void SelectSort1(int* arr, int size) {int p = 0, q = size-1;//p指向數組開頭，q指向數組最后一個位置while (p < q) {//當錯過或者相遇就結束int min = p, max = p;//迭代位置for (int i = p; i <= q; i++){if (arr[min] > arr[i])//找到最小值min = i;if (arr[max] < arr[i])//找到最大值max = i;}Swap(&arr[min], &arr[p]);//交換if (max == p)//5 2 3 4 1//判斷是否要糾正max = min;Swap(&arr[max], &arr[q]);//交換p++, q--;}
}
int main() {int arr[] = { 4,3,1,5,2 };SelectSort1(arr, sizeof(arr) / sizeof(arr[0]));Print(arr, sizeof(arr) / sizeof(arr[0]));return 0;
}

運行結果：

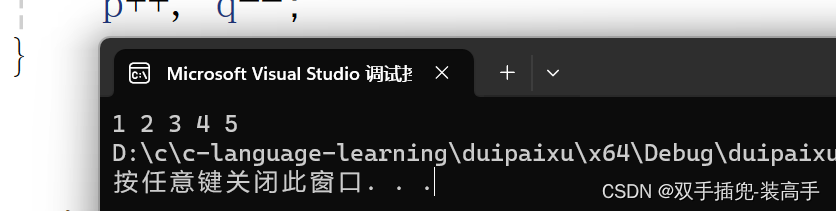
二、堆排序

堆：

結構性:用數組表示的完全二叉樹;
有序性:任一結點的關鍵字是其子樹所有結點的最大值(或最小值)
“最大堆(MaxHeap)”,也稱“大頂堆”，即最大值所有父親大于等于孩子
“最小堆(MinHeap)”,也稱“小頂堆”，即最小值所有父親小于等于孩子

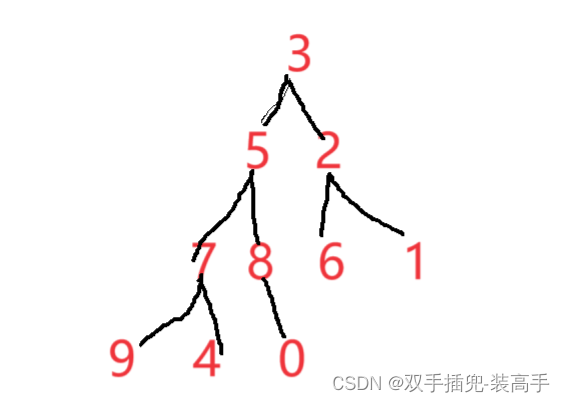
小堆:堆頂數據是最小的，并且所有節點都小于左右子樹

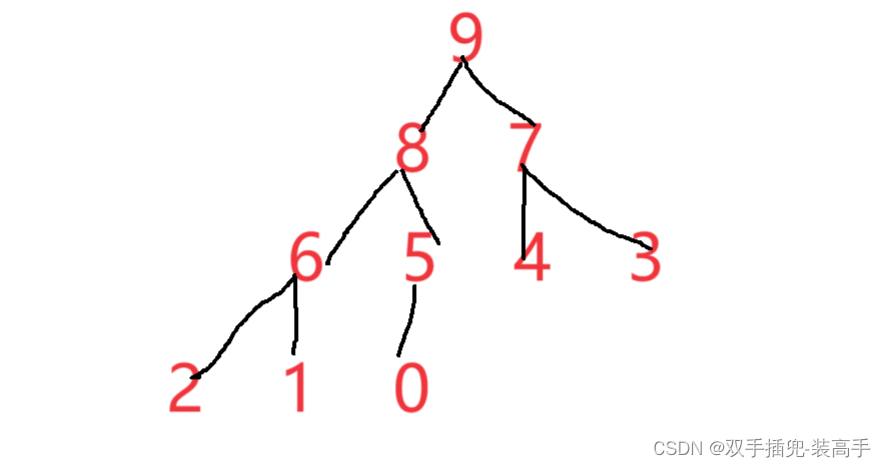
大堆:堆頂數據是最大的 ，并且所有節點都大于左右子樹

用堆來實現排序：
（1）使用向下調整算法：
前提：左右子樹必須是小堆或者大堆
作用：建堆
如：
左右子樹對比選擇，再與根比較

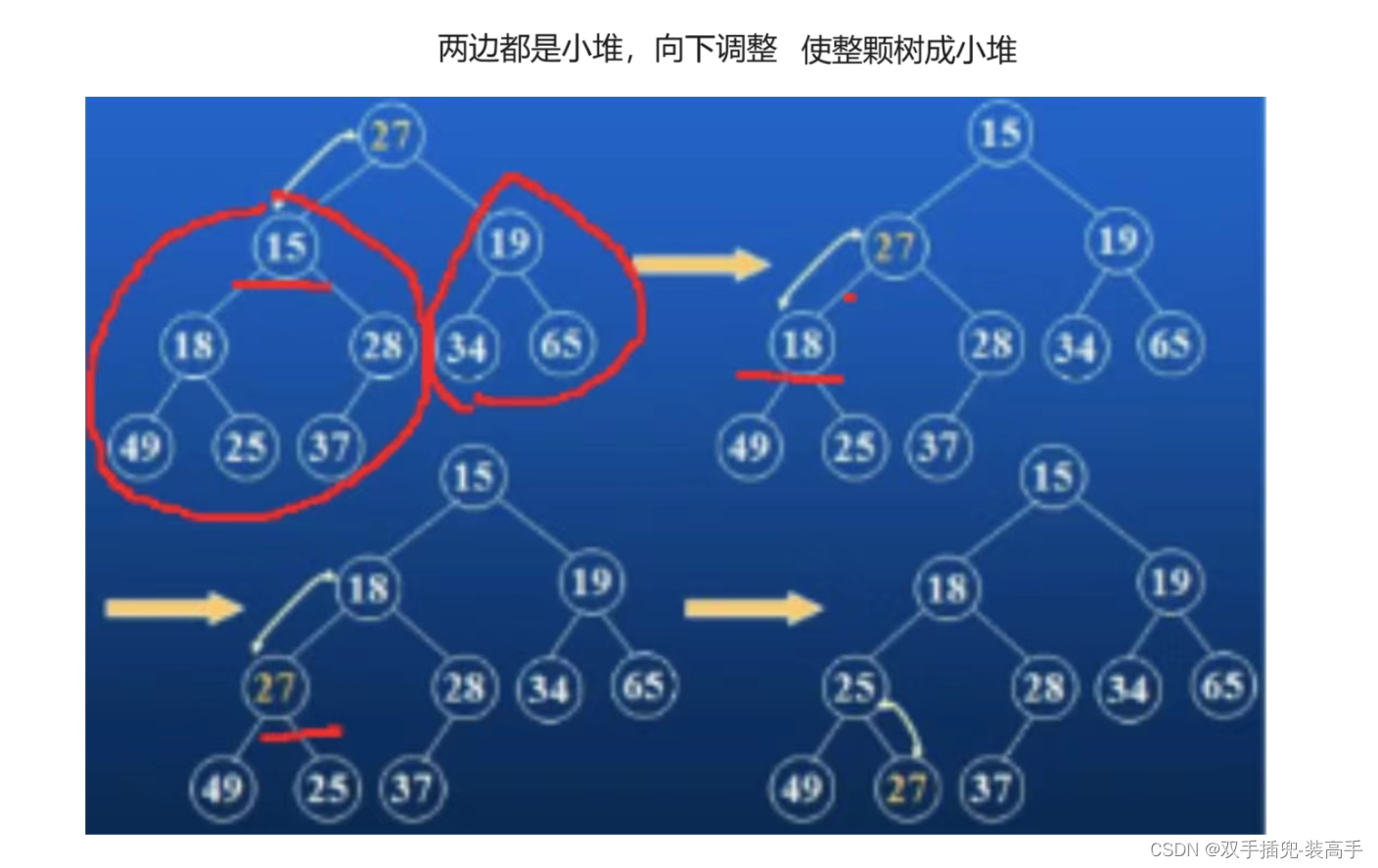
（2）建堆
當我們要實現升序時，通過向下調整法要建大堆
建的過程：因為使完全二叉樹，我們可以從最后非葉點節點開始建，直到沒有節點就結束。
如：
建大堆

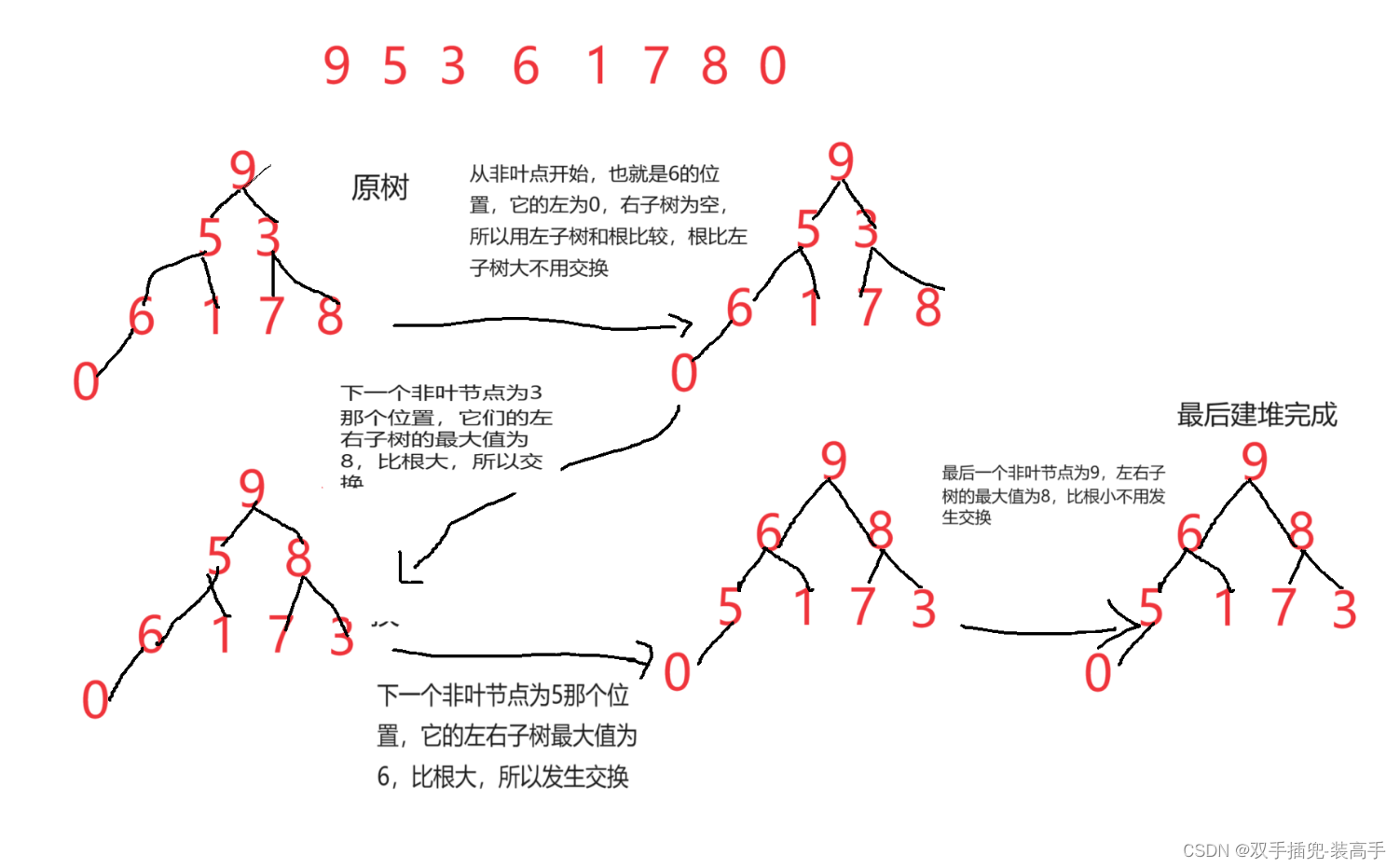
找左右子樹位置：

樹的左子樹的下標等于根的下標*2+1，的下標等于根的下標 *2+2

建完后，我們可以將最后一個元素和第一個元素交換，然后再做向下調整即可不用重新建堆了，再讓第一個元素和倒數第二個元素交換，以此類推…
為什么不建小堆呢？如果建小堆的話，用第一個根（最小值）就是數組的第一個元素了，我們不能動它，那么再讓數組的第二元素重新做根，但是這樣的話順序就會被打破，又要重新建堆了，那樣時間復雜度會提高（如何實現降序的話可以建小堆）

代碼實現：

//交換
void Swap(int* a,int* b) {int t = *a;*a = *b;*b = t;
}
//打印
void Print(int* arr, int n) {for (int i = 0;i < n; i++)printf("%d ", arr[i]);
}
//向下調整  大堆
void AdjustDwon(int *arr,int p,int size) {int q = p;//節點位置int z = q * 2 + 1;//節點左子樹，z+1就是右子樹的位置了while (z<size) {//當z大于數組長度時就說明該節點不存在左右子樹//判斷左右子樹大小，后面是判斷是否有右子樹if (arr[z] <arr[z + 1]&&z+1<size)z += 1;if (arr[z] > arr[q]) {//判斷是否比根大Swap(&arr[z], &arr[q]);q = z;z = q * 2 + 1;//迭代}elsebreak;}
}
void  HeapSort(int* arr,  int size) {//建堆，size-1-1就是除2（求子樹公式反過來用，最后減一是因為我們求的是下標）for (int i = (size - 1 - 1) / 2; i >= 0; i--) {AdjustDwon(arr, i, size);}int ned = size - 1;
//最后一個下標位置開始，和下標為0的元素交換，一直交換下去，并且交換一次就調整一次//當ned==1就證明排好了while (ned>0) {Swap(&arr[0], &arr[ned]);AdjustDwon(arr, 0, ned);//重新調整ned--;}
}int main() {int arr[] = { 4,3,1,5,2 };HeapSort(arr, sizeof(arr)/sizeof(arr[0]));Print(arr, sizeof(arr) / sizeof(arr[0]));
return 0}

運行結果：

三、時間復雜度

選擇排序：
n-1 ,n-2…2，1
是一個等差數列求前n-1項和，粗略來算就是n^2
所以時間復雜度為O（n^2）

堆排序：
建堆：O（n）

向下調整的時間復雜度為：
假設樹高為 h，樹的結點為n，因為n=2^h-1,那么h=log（n-1）（以2為底）
所以為O(logn-1)
我們還要進行n次這個向下調整（當然在進行的過程中n是會變化的）
那么總的次數n+nlogn
所以時間復雜度為O（nlogn）

四、穩定性

穩定性:

假定在待排序的記錄序列中，存在多個具有相同的關鍵字的記錄，若經過排序，這些記錄的相對次序保持不變，即在原序列中，r[i]=r[4]，且r[1]在r[4]之前，而在排序后的序列中，r[1]仍在r[4]之前，則稱這種排序算法是穩定的;否則稱為不穩定的。

選擇排序：不穩定
如：

堆排序：不穩定

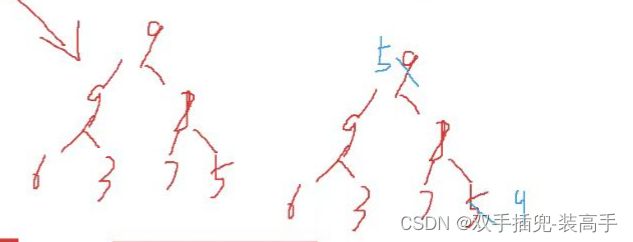
第一個9直接到最后了

以上就是我的分享了，如果有什么錯誤，歡迎在評論區留言。
最后，謝謝大家的觀看！