?
目錄
?
第一題:復寫零
第二題:快樂數:
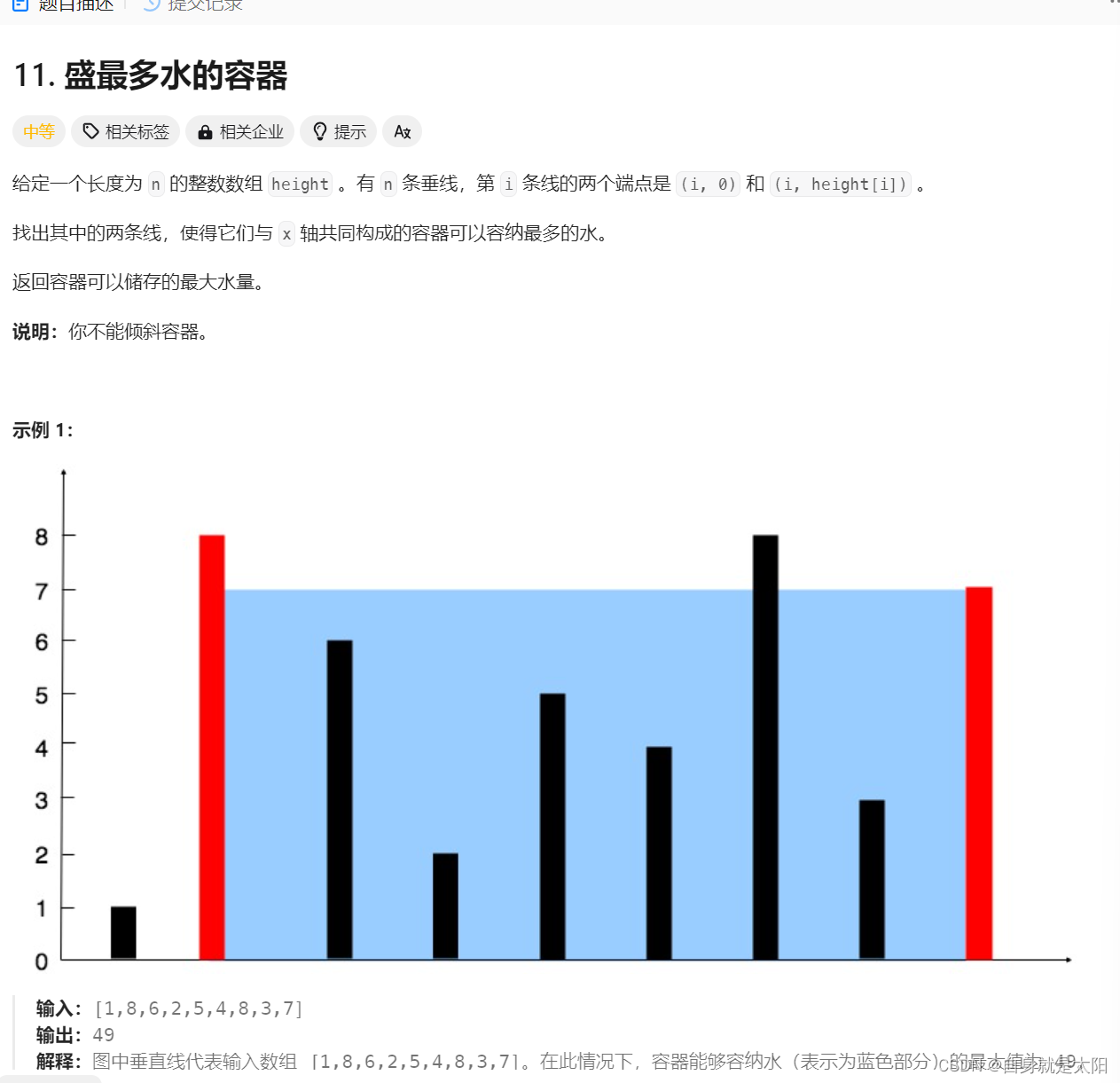
第三題:盛水最多的容器
第四題:有效三角形的個數
?
第一題:復寫零
力扣(LeetCode)官網 - 全球極客摯愛的技術成長平臺
 思路:
思路:
上期介紹到雙指針,這次來用雙指針實際操作。第一種從前往后復寫,會導致為復寫的數字被覆蓋,因此選擇從后往前復寫,那么先找到復寫的最后一個元素,再從后往前復寫即可。
步驟
1.初始化指針
2.找復寫
3.處理邊界問題
4.開始復寫
class Solution {
public:void duplicateZeros(vector<int>& arr) {int cur = 0, dest = -1, n = arr.size();
while (cur < n)
{if (arr[cur]) dest++;//說明不用復寫else dest += 2;if (dest >= n - 1)break;cur++;
}
//出來的時候cur就是莫位置
//處理邊界
if (dest == n)
{arr[n - 1] = 0;cur--; dest -= 2;
}
//從后往前面復寫
while (cur >= 0)
{if (arr[cur])//非0arr[dest--] = arr[cur--];else//為0{arr[dest--] = 0;arr[dest--] = 0;cur--;}
}}
};第二題:快樂數:
力扣(LeetCode)官網 - 全球極客摯愛的技術成長平臺

?
思路:
這題通過在紙上演算可以發現,給定一個數他按照快樂數的定義,要么演變到1,要么將會重復他在演變過程中的一個數字,具體大家可以在紙上推算一遍
即
:
class Solution
{
public:int bitSum(int n)int sum = 0;while (n){int t = n % 10;sum += t * t;n /= 10;}bool isHappy(int n){int slow = n, fast = bitSum(n);while (slow != fast){slow = bitSum(slow);fast = bitSum(bitSum(fast));}return slow == 1;}
};第三題:盛水最多的容器
力扣(LeetCode)官網 - 全球極客摯愛的技術成長平臺
 思路:
思路:
第一想法就是暴力枚舉
s=h(高)*w(寬度)
即弄兩個for循環,依次求出面積,再比較最大值,這樣時間復雜度為n的平方會超時,因此
第二種就是雙指針,觀察發現,面積的高是由左右兩邊的低邊界為準。就以上圖為例,高是由右邊那條高決定,左邊高往右移動由于w一定減小,h要么減小要么不變,那么面積一定減小,所以我們就從兩個邊界開始來移動,記錄每一次的面積,返回最大即可
注意,每次移動的是那個h小的,因為大h移動,s要么減少要么不變,而我們求的是最大的。
第一種:暴力求解
class Solution {
public:int maxArea(vector<int>& height) {int n = height.size();int ret = 0;// 兩層 for 枚舉出所有可能出現的情況for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {// 計算容積,找出最?的那?個ret = max(ret, min(height[i], height[j]) * (j - i));}}return ret;}
};第二種:
對撞指針:
class Solution
{
public:int maxArea(vector<int>& height){int left = 0, right = height.size() - 1, ret = 0;while (left < right){int v = min(height[left], height[right]) * (right - left);ret = max(ret, v);// 移動指針if (height[left] < height[right]) left++;else right--;}return ret;}
};
第四題:有效三角形的個數
力扣(LeetCode)官網 - 全球極客摯愛的技術成長平臺
 思路:
思路:
在判斷一個三角形時,如果對于一對升序數組a,b,c
如果a+b>c那么即可構成三角形,不需要判斷三次
原因,如果上述條件成立那么,b+c>a,a+c>b一定成立,因為c是最大的數
第一思路就是暴力求解,先把給定數組排序,然后從第一個元素開始遍歷,用三個for循環實現,但是時間復雜度較大,運行會超時
class Solution {
public:int triangleNumber(vector<int>& nums) {// 1. 排序sort(nums.begin(), nums.end());int n = nums.size(), ret = 0;// 2. 從?到?枚舉所有的三元組for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {for (int k = j + 1; k < n; k++) {// 當最?的兩個邊之和?于第三邊的時候,統計答案if (nums[i] + nums[j] > nums[k])ret++;}}}return ret;}
};應次這里換一種高效方法就是用雙指針來實現,因為已經排完升序,依據暴力解法,可以先固定一條最長邊,然后找出比這條邊小的二元組,讓著個二元組的和大于最長邊,即可利用對撞指針來實現。
class Solution
{
public:int triangleNumber(vector<int>& nums){// 1. 優化sort(nums.begin(), nums.end());// 2. 利?雙指針解決問題int ret = 0, n = nums.size();for (int i = n - 1; i >= 2; i--) // 先固定最?的數{// 利?雙指針快速統計符合要求的三元組的個數int left = 0, right = i - 1;while (left < right){if (nums[left] + nums[right] > nums[i]){ret += right - left;right--;}else{left++;}}}return ret;}
};
?
?
)



——JavaScript監聽按鍵,禁止F12,禁止右鍵,禁止保存網頁【Ctrl+s】等操作)






![[Linux] nginx的location和rewrite](http://pic.xiahunao.cn/[Linux] nginx的location和rewrite)







)