題目描述

110.平衡二叉樹

給定一個二叉樹，判斷它是否是高度平衡的二叉樹。

本題中，一棵高度平衡二叉樹定義為：

一個二叉樹每個節點 的左右兩個子樹的高度差的絕對值不超過 1 。

示例 1：

輸入：root = [3,9,20,null,null,15,7]
輸出：true

示例 2：

輸入：root = [1,2,2,3,3,null,null,4,4]
輸出：false

示例 3：

輸入：root = []
輸出：true

提示：

• 樹中的節點數在范圍 [0, 5000] 內
• -104 <= Node.val <= 104

解題思路

二叉樹節點的高度：從根節點到該節點的最長簡單路徑邊的條數

二叉樹節點的深度：從該節點到葉子節點的最長簡單路徑變的條數

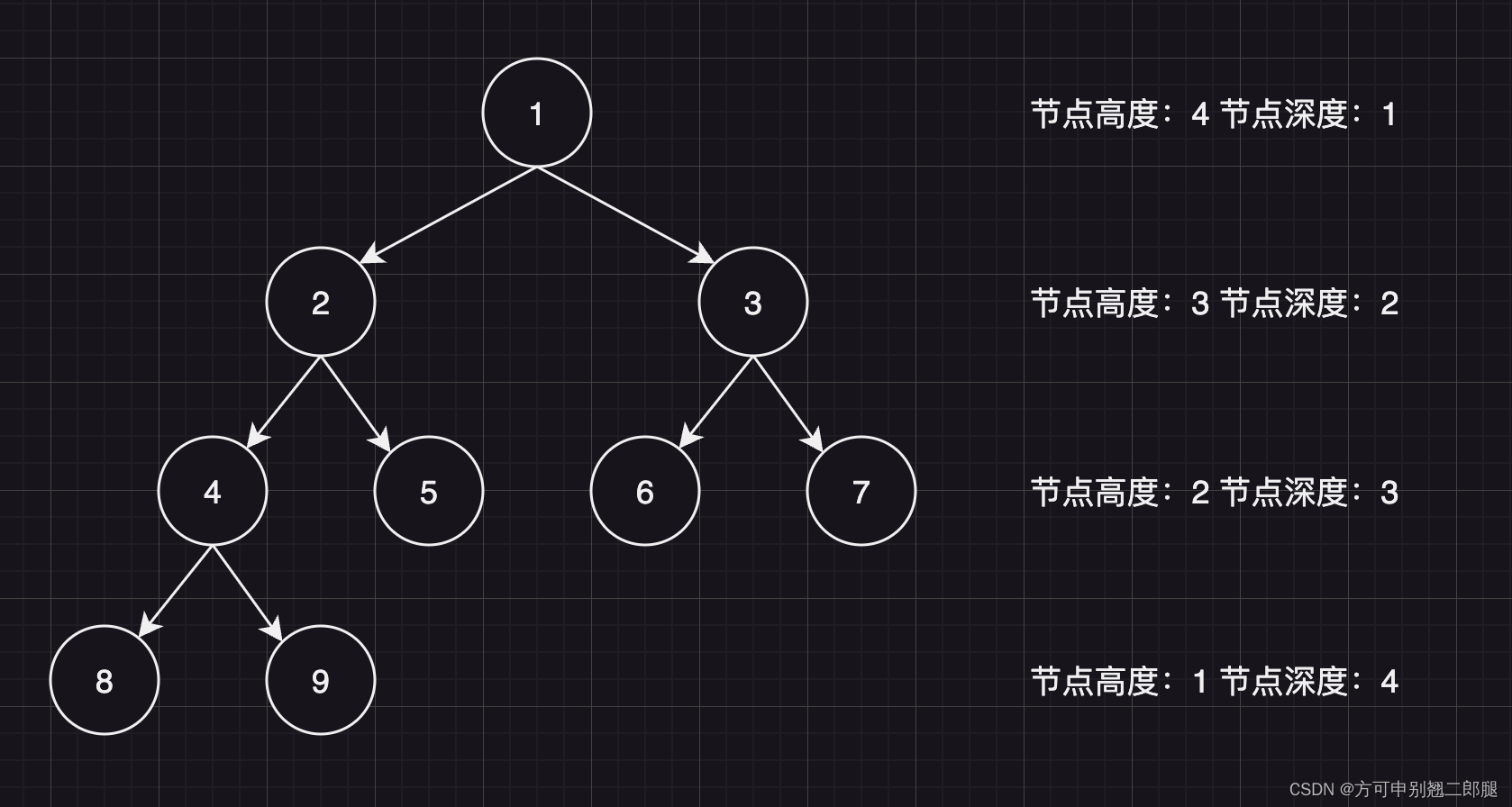
求深度可以從上到下去查詢，所以需要前序遍歷，而求高度只能從下到上去查，只能后序遍歷。

因此本題使用后序遍歷。

遞歸

遞歸三部曲

1. 確定遞歸函數的參數和返回值
   參數：當前傳入的節點
   返回值：因為求的是高度，所以為int

   如果當前傳入節點為根節點的二叉樹已經不是二叉平衡樹了，還返回高度的話就沒有意義了。

   所以如果已經不是二叉平衡樹了，可以返回 -1 來標記已經不符合平衡樹的規則了。

   int getHeight(TreeNode* node)
   

2. 確定終止條件
   遇到空節點時終止，返回0，表示當前節點為根節點的樹高度為 0

   if (node == NULL) {return 0;
   }
   

3. 確定單層遞歸的邏輯
   分別求出左右子樹的高度，如果差值小于等于 1 ，則返回當前二叉樹的高度，否則返回 -1，表示已經不是平衡二叉樹了。

   int leftHeight = getHeight(node->left);
   if (leftHeight == -1) return -1;
   int rightHeight = getHeight(ndoe->right);
   if (rightHeight == -1) return -1;
   int result;
   if (abs(leftHeight - rightHeight) > 1) {result = -1;	
   } else {result = 1 + max(leftHeight, rightHeight);
   }
   return result;
   

迭代

本題的迭代方式可以先定義一個函數，專門用來求高度。

這個函數通過棧模擬的后序遍歷找每一個節點的高度（其實是通過求傳入節點為根節點的最大深度來求的高度）

// cur節點的最大深度，就是cur的高度
int getDepth(TreeNode* cur) {stack<TreeNode*> st;if (cur != NULL) st.push(cur);int depth = 0; int result = 0;while (!st.empty()) {TreeNode* node = st.top();if (node != NULL) {st.pop();st.push(node);st.push(NULL);depth++;if (node->right) st.push(node->right);if (node->left) st.push(node->left);} else {st.pop();node = st.top();st.pop();depth--;}result = result > depth ? result : depth;}return result;
}

然后再用棧來模擬后序遍歷，遍歷每一個節點的時候，再去判斷左右孩子的高度是否符合，代碼如下:

bool isBalanced(TreeNode* root) {stack<TreeNode*> st;if (root == NULL) return true;st.push(root);while (!st.empty()) {TreeNode* node = st.top();st.pop();if (abs(getDepth(node->left) - getDepth(node->right)) > 1) {return fasle;}if (node->right) st.push(node->right);if (node->left) st.push(node->left);}return true;
}

當然此題用迭代法，其實效率很低，因為沒有很好的模擬回溯的過程，所以迭代法有很多重復的計算。

雖然理論上所有的遞歸都可以用迭代來實現，但是有的場景難度可能比較大。

例如：都知道回溯法其實就是遞歸，但是很少人用迭代的方式去實現回溯算法！

因為對于回溯算法已經是非常復雜的遞歸了，如果再用迭代的話，就是自己給自己找麻煩，效率也并不一定高。

代碼實現

遞歸法

class Solution {
public:int getHeight(TreeNode* node) {if (node == NULL) return 0;int leftHeight = getHeight(node->left);if (leftHeight == -1) return -1;int rightHeight = getHeight(node->right);if (rightHeight == -1) return -1;return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftheight, rightHeight);}bool isBalanced(TreeNode* root) {return getHeight(root) == -1 ? false : true;}
};

迭代法

class Solution {
public:
class Solution {
private:int getDepth(TreeNode* cur) {stack<TreeNode*> st;if (cur != NULL) st.push(cur);int depth = 0; // 記錄深度int result = 0;while (!st.empty()) {TreeNode* node = st.top();if (node != NULL) {st.pop();st.push(node);                          // 中st.push(NULL);depth++;if (node->right) st.push(node->right);  // 右if (node->left) st.push(node->left);    // 左} else {st.pop();node = st.top();st.pop();depth--;}result = result > depth ? result : depth;}return result;}public:bool isBalanced(TreeNode* root) {stack<TreeNode*> st;if (root == NULL) return true;st.push(root);while (!st.empty()) {TreeNode* node = st.top(); st.pop();if (abs(getDepth(node->left) - getDepth(node->right)) > 1) {return false;}if (node->right) st.push(node->right);           // 右（空節點不入棧）if (node->left) st.push(node->left);             // 左（空節點不入棧）}return true;}
};