abstract

• 除了圓和圓錐曲線外,還有許多曲線用極坐標描述會簡單得多

典型曲線

• 分析下列曲線時,線分析是否含有三角函數(周期性)

• 利用描點法做出單個周期內的圖形

• 作圖:可以打開geogebra

  • https://www.geogebra.org/calculator/fds4duvm

  • 

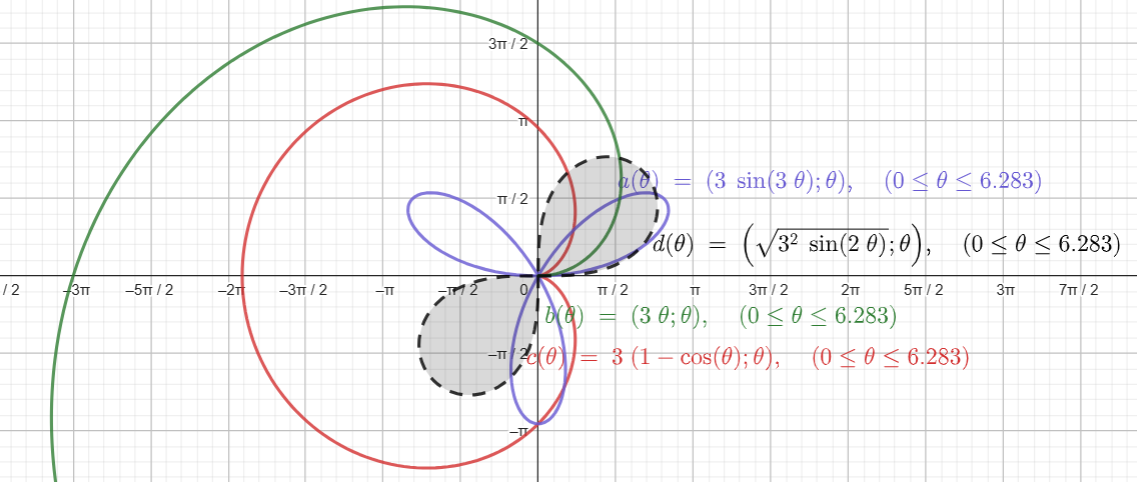
心形線

• $r$=$a(1?\cos \theta )$,$(a>0)$
  • 周期$T$=$2\pi$
  • 奇偶性:偶函數,圖形關于極軸對稱$(r,\theta )$,$(r,2\pi ?\theta )$同時位于圖形上
  • 綜上,只要考慮$[0,\pi ]$上的圖形,就可以通過翻折圖形,的到整個周期的圖形
  • 而在$[0,\pi ]$上,$\cos \theta$是從$1\to 0\to ?1$的遞減函數,前半程是凸函數,后半程是凹函數;
    • 從而$1?\cos \theta$從$0\to 1\to 2$是一個遞增的過程,因此$a(1?\cos \theta )$從$0\to 2a$

玫瑰線

• $r$=$a\sin 3\theta$,$(a>0)$ 三葉玫瑰線

  • 周期為$T=2\pi /3$,作圖時考慮$[0,\frac{2\pi }{3}]$內的區間;根據周期性,就可以直接得到$[\frac{2\pi }{3},\frac{4\pi }{3}]$以及$[\frac{4\pi }{3},2\pi ]$內的圖形

  • $t=3\theta$	0	$\frac{\pi }{4}$	$\frac{\pi }{2}$	$\frac{3}{4}\pi$	$\pi$	$\frac{5}{4}\pi$	$\frac{3}{2}\pi$	$\frac{7}{4}\pi$	$2\pi$
    $\theta$	$0$	$\frac{1}{12}\pi$	$\frac{\pi }{6}$	$\frac{1}{4}\pi$	$\frac{1}{3}\pi$	$\frac{5}{12}\pi$	$\frac{1}{2}\pi$	$\frac{7}{12}\pi$	$\frac{2}{3}\pi$
    $r$=$a\sin 3\theta$	$0$	$\frac{\sqrt{2}}{2}a$	$a$	$\frac{\sqrt{2}}{2}a$	0	$?\frac{\sqrt{2}}{2}a$	$?a$	$?\frac{\sqrt{2}}{2}a$	$0$

  • 通過描點可以發現,該圖形在$[0,\frac{2}{3}\pi ]$內會產生2片葉子;若將其放直角坐標系上,極點和極軸正方向分別和直角坐標系重合,則第一片葉子落在區間$[0,\frac{\pi }{3}]$;第二片葉子落在$[\frac{4}{3}\pi ,\frac{5}{3}\pi ]$;每片葉子占據$\frac{1}{3}\pi$的弧度,從順時針的角度看,兩片葉子相距$\frac{4}{3}\pi$,從順時針看,兩片葉子相距$2\pi ?\frac{4}{3}\pi =\frac{2\pi }{3}$

阿基米德螺線

• $r=a\theta$,$(a>0,\theta ?0)$
  • 這個曲線的極坐標方程形式很簡單,一個常系數$a$和極角$\theta$的乘積
  • $r$隨著$\theta$的增大而增大

伯努利雙扭線

• 有兩種常見形式:

  1. $r^2$=$a^2\cos 2\theta$,$(a>0)$
  2. $r^2$=$a^2\sin 2\theta$,$(a>0)$

• 分析

  • 定義域:
    • 考慮到$r^2?0$,$a^2?0$,則對于形式1,2分別要求$\cos 2\theta ,\sin 2\theta ?0$
      • 以形式(2)為例,$\sin 2\theta ?0$,從而$t=2\theta \in [2k\pi ,\pi +2k\pi ]$,即$\theta \in [k\pi ,\frac{\pi }{2}+k\pi ]$
      • 容易發現圖形是不連續的某些$\theta$區間上沒有定義
  • 周期性:$T=\pi$
  • 奇偶性:
    • 形式(1)是偶函數,圖形關于極軸對稱
    • 形式(2)是奇函數,圖形關于極點對稱
  • 兩種形式的關系:$\sin (\theta +\frac{\pi }{2})$=$\cos \theta$;則$\sin (2\theta +\frac{\pi }{2})$=$\cos 2\theta$,即$\sin 2(\theta +\frac{\pi }{4})$=$\cos \theta$,
    • 這意味著將圖形(2)往負角方向旋轉,即順時針旋轉$\frac{\pi }{4}$,就能得到圖形(1)
    • 這和直角坐標系上的圖形的$f(x+a)$是$f(x)$往$x$軸負方向移動類似(“負加正減,負向移動加,正向移動間”)

• 以形式(2)為例分析

  • 考慮到周期為$\pi$,我們研究$\theta \in [0,\pi ]$內即可,又考慮到定義域,因此我們在$\theta \in [0,\frac{\pi }{2}]$上研究

  • 為了描點,將方程(2)變形為$r$=$a\sqrt{\sin 2\theta }$

  • $\theta$	$0$	$\frac{\pi }{8}$	$\frac{\pi }{4}$	$\frac{3}{8}\pi$	$\frac{1}{2}\pi$
    $t=2\theta$	$0$	$\frac{\pi }{4}$	$\frac{\pi }{2}$	$\frac{3}{4}\pi$	$\pi$
    $r$	$0$	$\sqrt{\frac{\sqrt{2}}{2}}a$	$a$	$\sqrt{\frac{\sqrt{2}}{2}}a$	$0$

  • 從單調性分析:$\sin 2\theta$在$2\theta \in [0,\pi ]$上的變化為:$[0,\frac{\pi }{2}]$遞增,$[\frac{\pi }{2},\pi ]$上遞減;相應的,$\theta$區間$[0,\frac{\pi }{4}]$,$[\frac{\pi }{4},\frac{\pi }{2}]$上分別遞增和遞減,這就是$r$的變換規律