資料來源：

https://www.youtube.com/watch?v=Ye018rCVvOo&list=PLJV_el3uVTsMhtt7_Y6sgTHGHp1Vb2P2J&index=1

https://www.youtube.com/watch?v=bHcJCp2Fyxs&list=PLJV_el3uVTsMhtt7_Y6sgTHGHp1Vb2P2J&index=2

分三步

1、 定義function

b和w是需要透過知識去獲取的，是未知的

做機器學習，需要Domain Knowledge，這些知識就是用來解b和w

這里的函式，就叫做Model

我們知道2月25號的人數是多少，就叫feauture

2、 定義Loss

Loss is a function of parameters

真實的值叫Label（正確的數值）

可以算出來最近3年的誤差，把所有的誤差加起來，算出來一個L，這就是我們的Loss，值越大，說明越不好

MAE和MSE的區別和選擇具體而定，還有Cross-entropy

真實的后臺統計數據例子

越偏紅色，代表Loss越大，偏藍色，Loss越小，那在預測的時候，w為0.75 b代500，可能預測會更準

3、最佳化算法

做法： Gradient Descent

如何做： 當w不同的值時，會得到不同的Loss，

怎么找到w，讓Loss最小，隨機選取初始化的點 w0（有一些方法可以更科學的找到這個值）

計算w對l的微積分，計算error surface的斜率，如果這個斜率的值為負數，

把w的值變大，Loss就會小

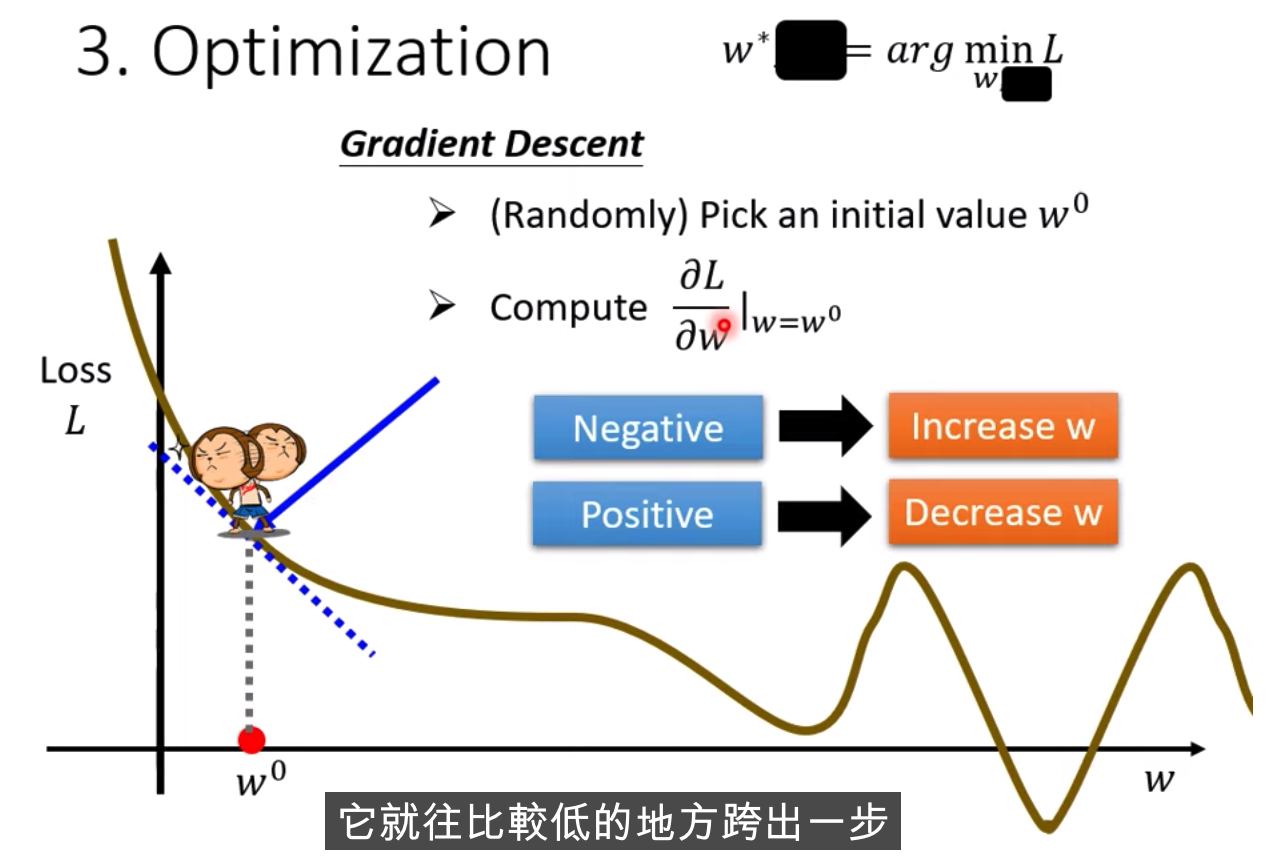
跨步要多大呢？

斜率大，就跨大

學習速率是自己設定的

Loss的值為什么會是負數？

因為這個函數是自己定義的，Loss的定義的估算的值和實際的值的絕對值，如果根據剛剛的定義，不可能為負數

但上面的這個例子不是真實的案例，error surface 可能是任何形狀

hyperparameter，自己設定的

什么時候會停止下來？一般兩種情況

a、 前期設定了這個參數，例如次數

b、 達到了理想的狀態

Gradient Descent上面找不到最佳的loss值，因為隨機的位置不一樣

Local minima是個假的問題，具體為什么，后面會講

兩個參數，如何做上面的Graddient Descent？

例子

課程總結：

這三個步驟合并起來，叫做訓練

2021年的誤差還是比較大的，怎么做的更好？ 分析下數據

藍色線相當于把紅色右移了一天而已，每隔7天就是一個循環

這個model是一個比較壞的，我們可以拿7天的周期來進行修改

x叫做feature

上面的叫做Linear Model，我們后面看下怎么把Linear Model做的更好

Linear Model 太過簡單了

我們需要寫出更復雜，更多未知參數的function

1除以1+Exponential-b+wx1，再乘以constant常數

當b+wx1趨向于無窮大的時候，會發生什么事呢，Exponential會消失，當X1非常大的時候，這一條線會收斂在高度是C的地方

當b+wx1趨向于負的無窮大，分母會非常大，Y的值會趨近于0

S型的function，叫做sigmoid

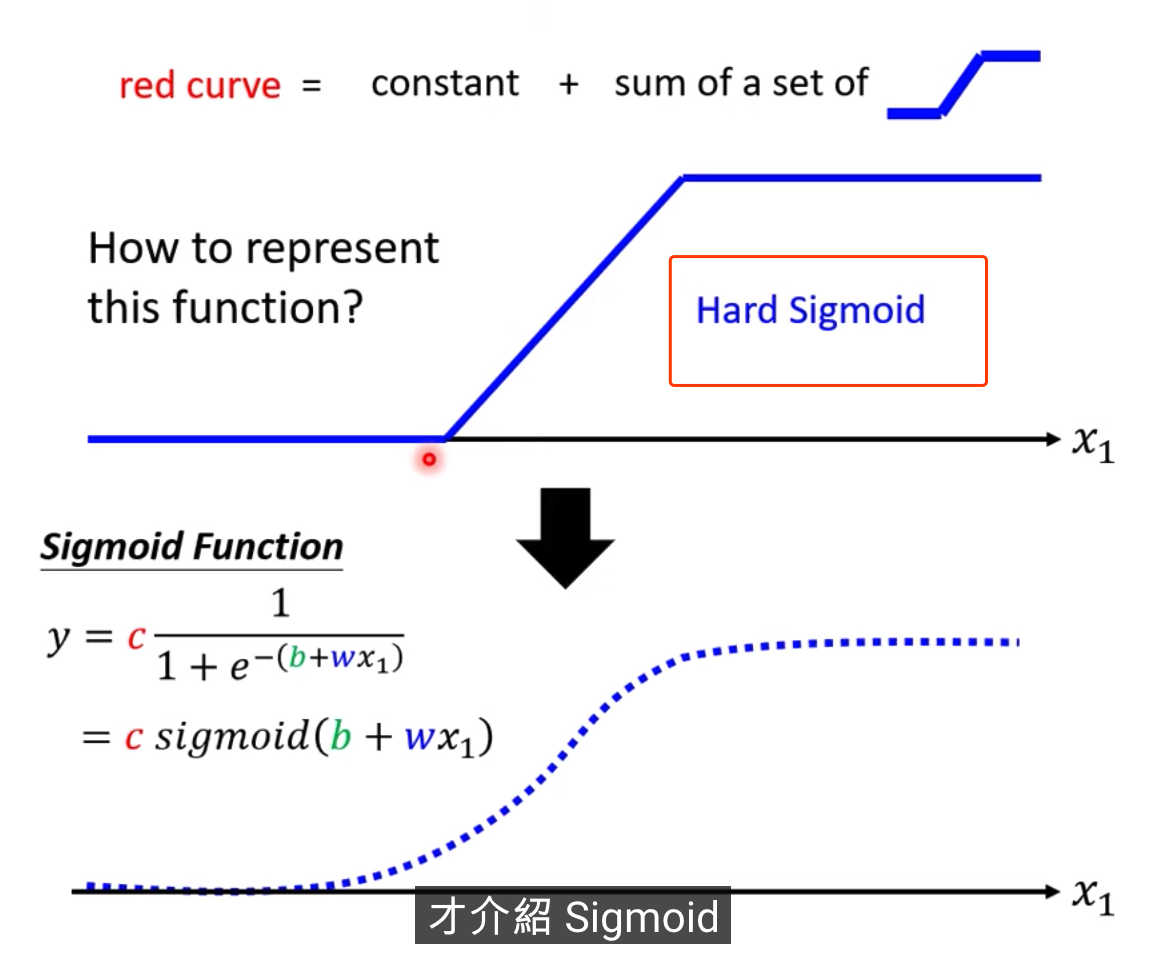
我們需要各式各樣合適藍色的function，那這個藍色function怎么出來呢，需要調整b和w

改w，會改變斜率，斜坡的坡度

修改b呢，會左右移動

修改c，會改變高度

可以制造出不同

把0和1和2和3都加起來

summation，b是constant

假設b,c,w是未知參數，有彈性，有未知參數的函式

Transpose

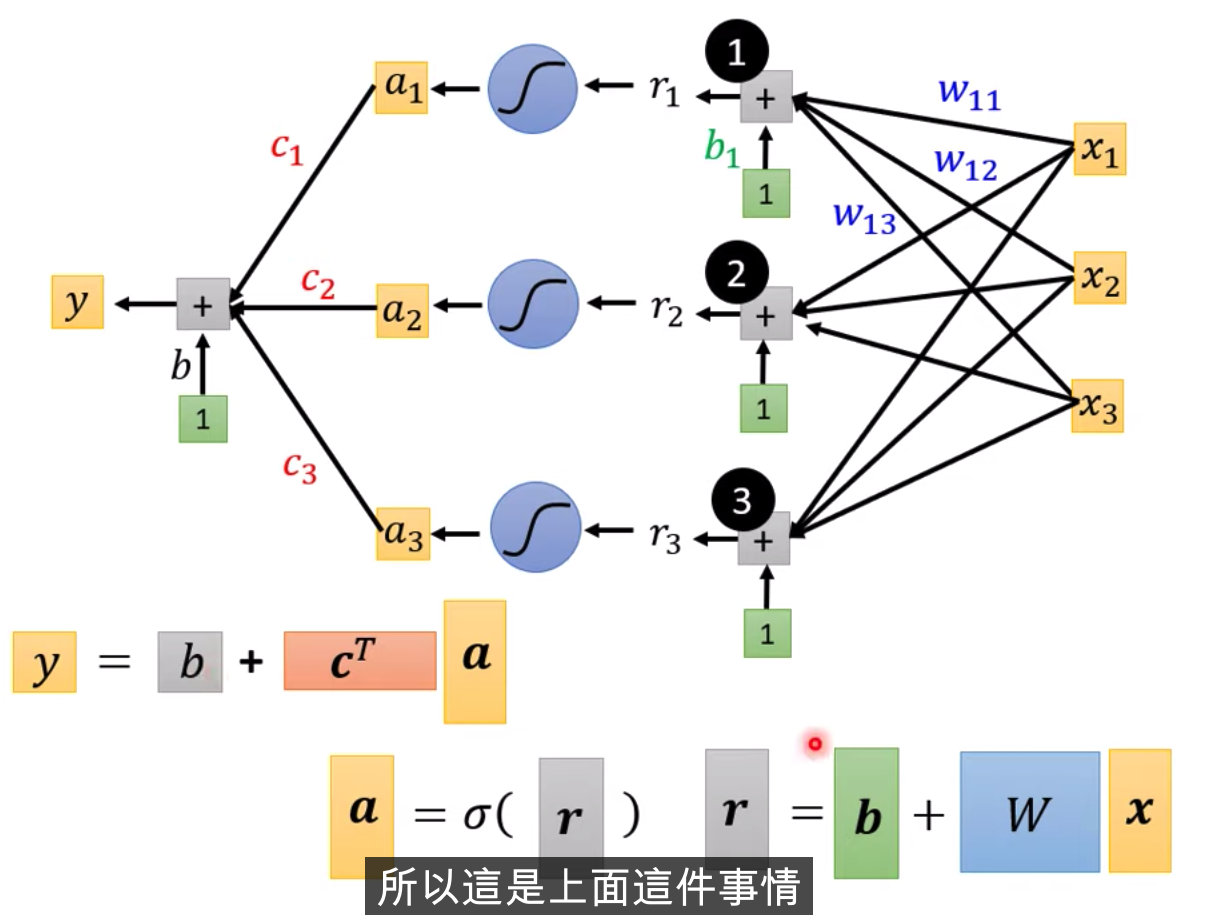
X輸入，我們的Feature是X這個向量，X乘上矩陣W加上向量b，得到向量r，再把向量r，通過Sigmooid Function得到向量a，

再把向量a跟乘上c的Transpose加上b，就得到了y

不同的表示方式，上面是圖示化的方式，下面是線性代數的表示方式

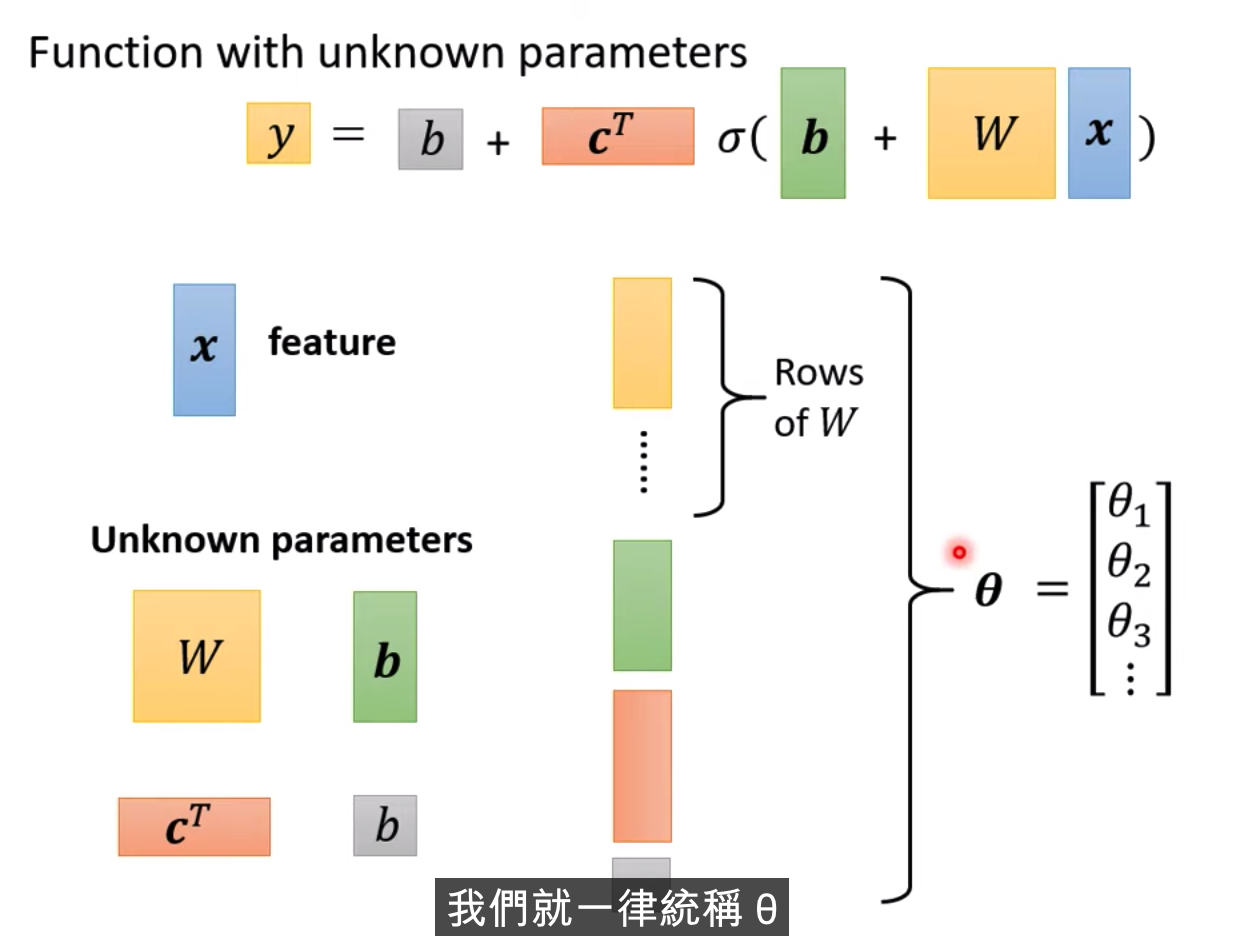
在參數小的情況下，窮舉所有的可能就行，不需要使用Gradient Descent

Sigmoid 可以有多個，會產生越多線段的 Piecewise Linear的function，你就可以逼近越復雜的function

至于需要幾個Sigmoid，這是另外的Hyper Parameter，這個自己決定

Loss function

Update和Epoch是不一樣的東西

每次更新一次參數叫做一次update，把所有的Batch都看過一遍，叫做一個Epoch

為什么要分成一個一個的batch？

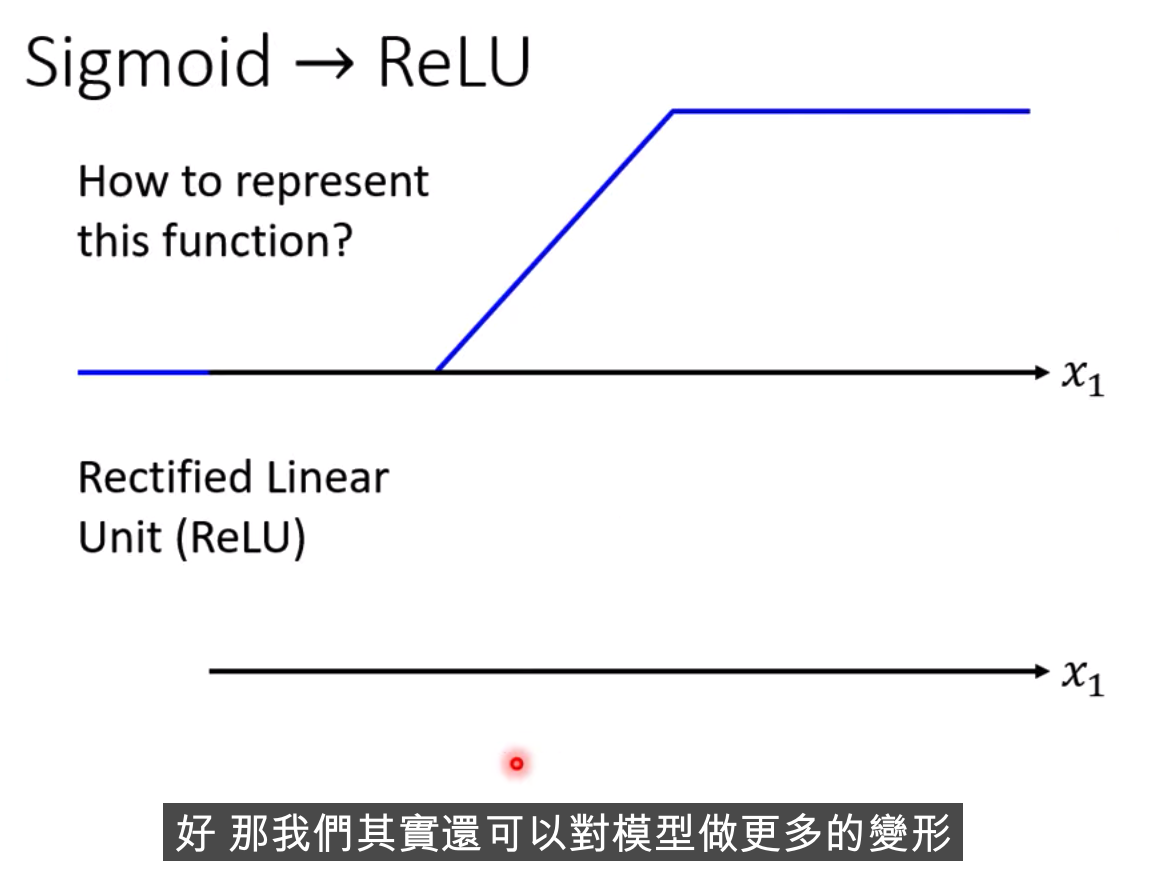
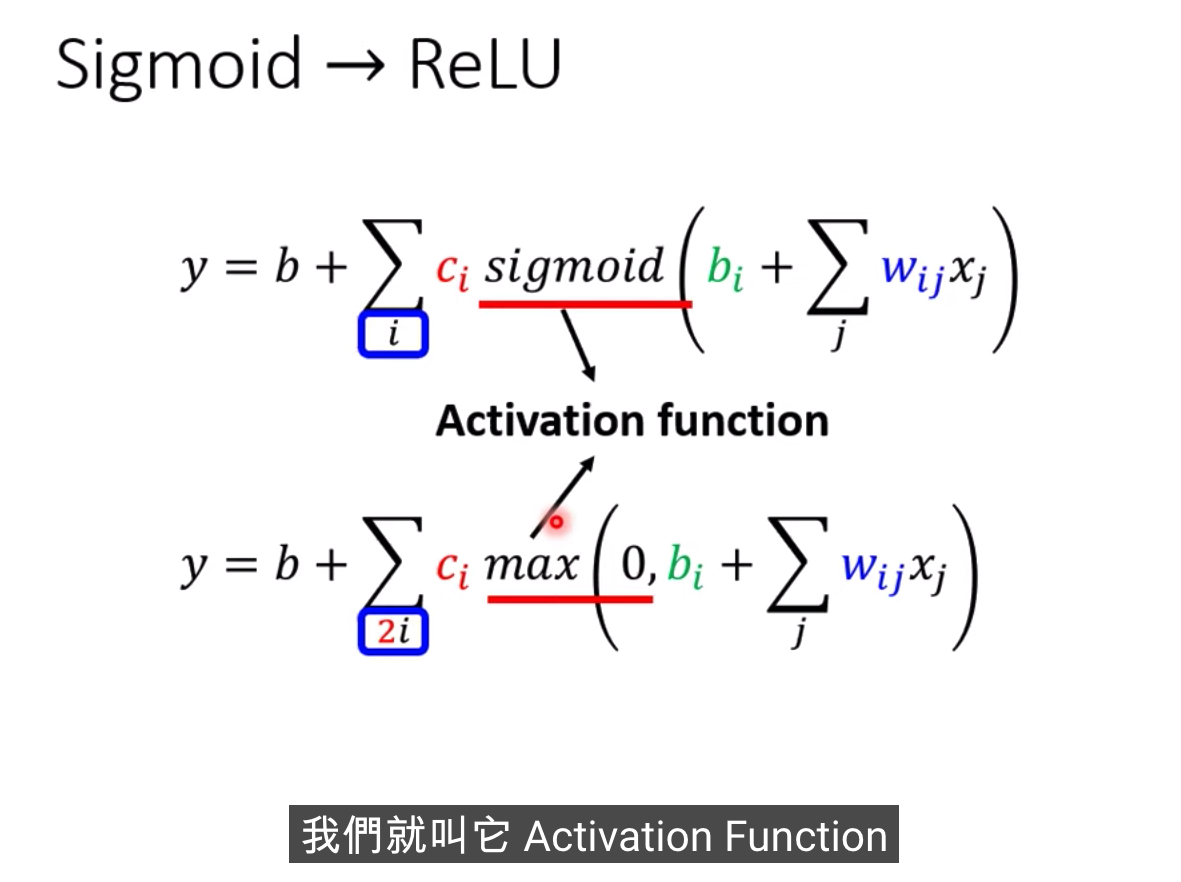
激活函數

哪種比較好？？ Relu好一些

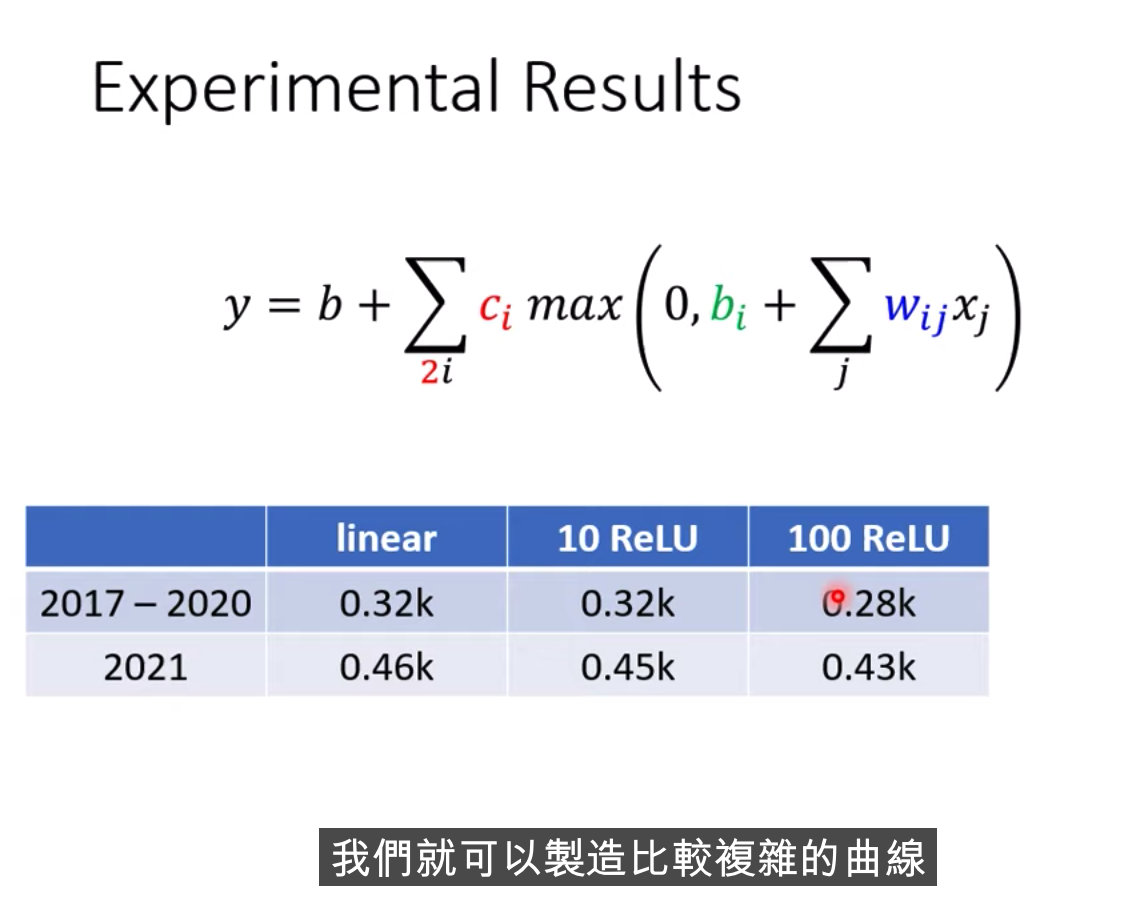
我們還可以繼續改我們的模型

我們可以把重復的事情，反復的再多做幾次，這里的幾次，又是另外一個超參數

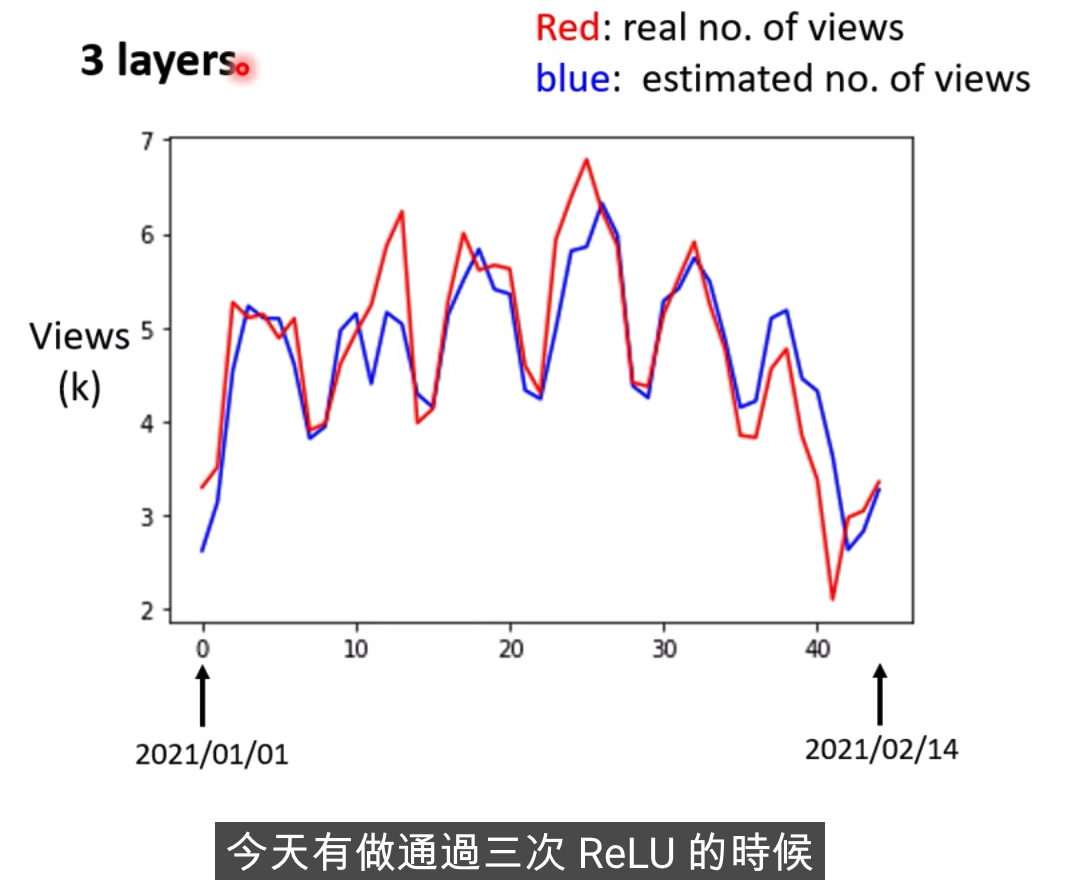
模型也需要一個好的名字

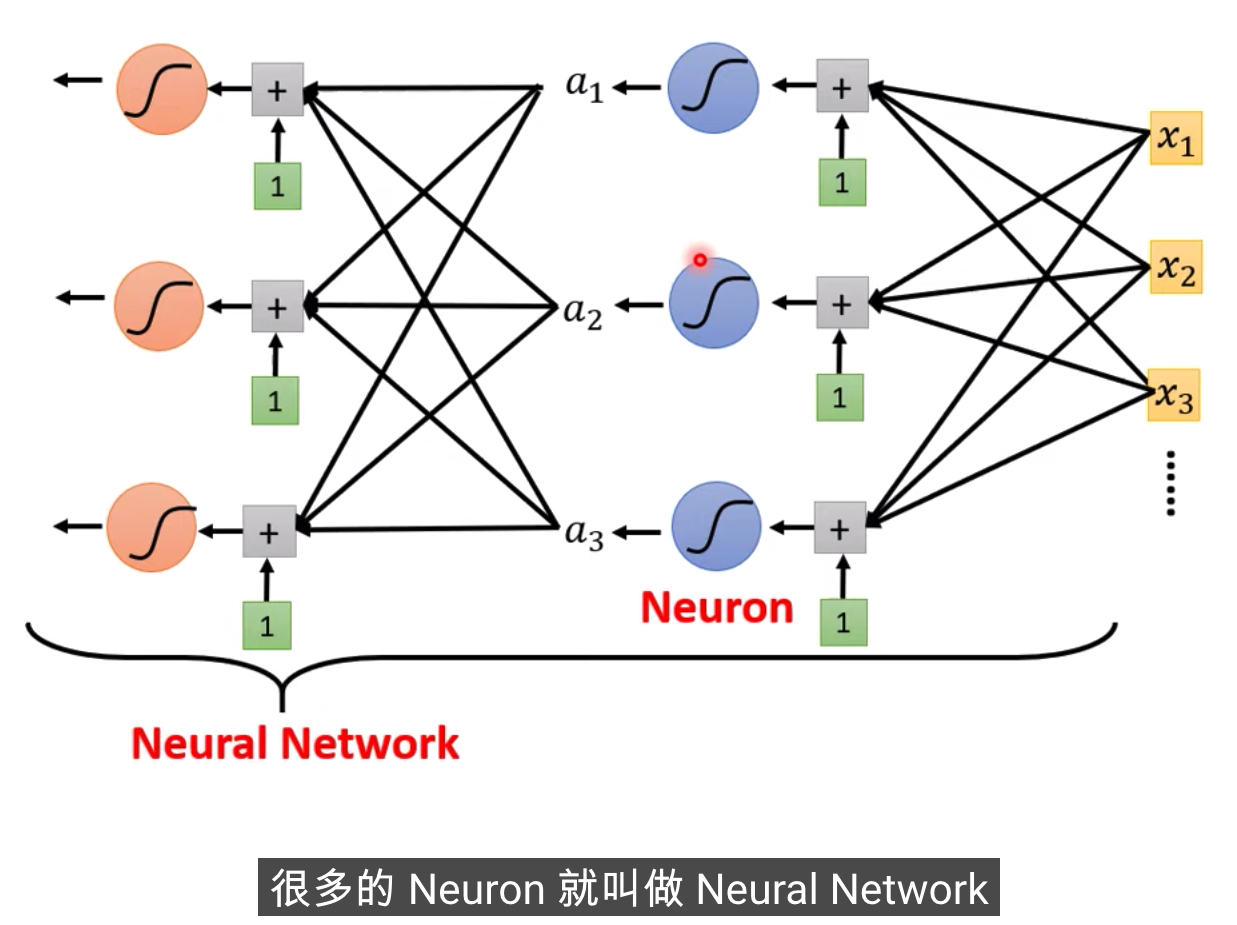
這個是在模擬人腦

Deep Learning的由來。。。。

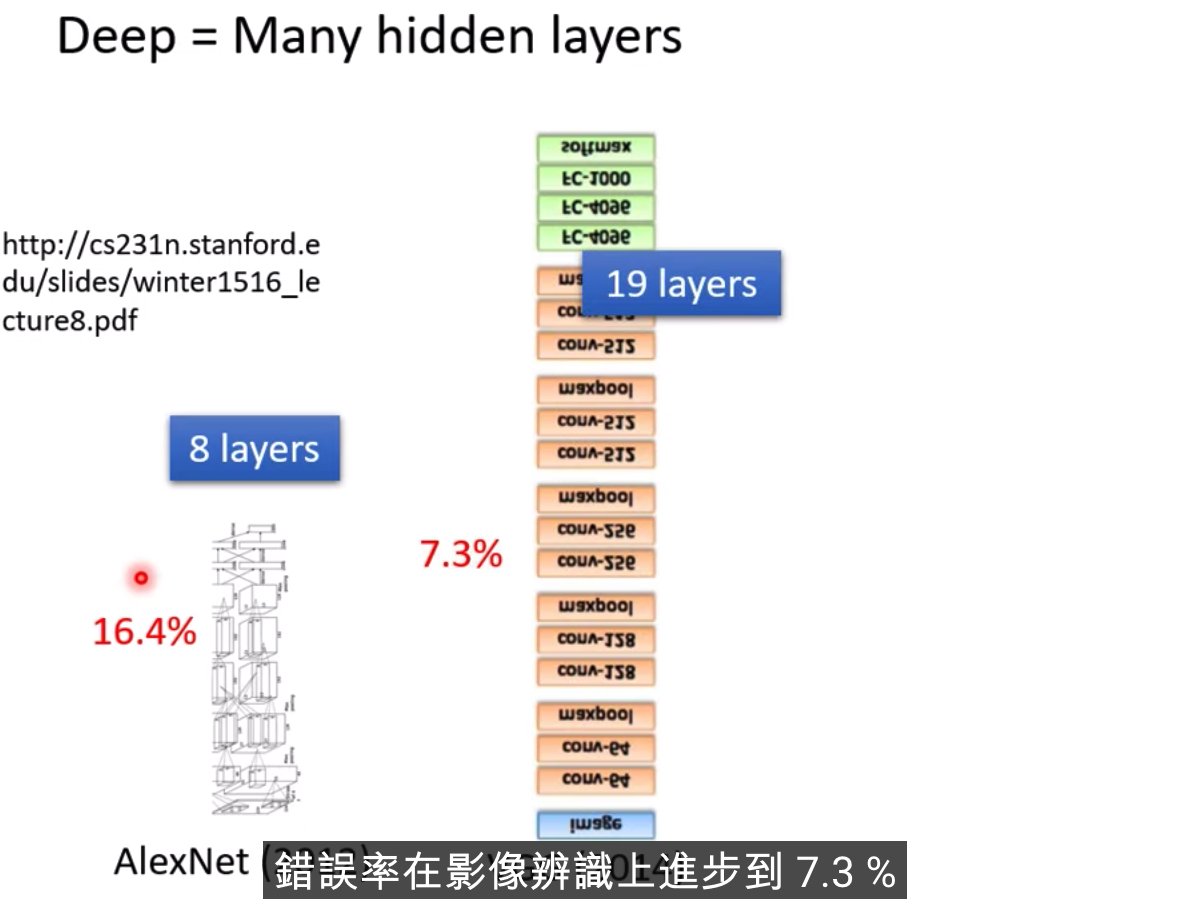
只要有足夠多的ReLU或者Sigmoid，就能夠逼近任何連續的Function

反復用的意義在哪里？

過多的層數效果不一定好

神經網絡結構那部分講的太精彩了。從簡單的線性回歸開始，到用幾個簡單線性函數去逼近一個分段線性函數，然后提出用sigmooid和線性逼近曲線，然后自然而然引出神經網絡的基本結構。輸入特征，參數，激活函數..等等概念自然而然都出來了