【數據結構高階】紅黑樹

目錄

一、紅黑樹的概念

二、紅黑樹的性質

2.1 紅黑樹與AVL樹的比較

三、紅黑樹的實現

3.1 紅黑樹節點的定義

3.2 數據的插入

3.2.1 紅黑樹的調整思路

3.2.1.1?cur為紅，f為紅，g為黑，u存在且為紅

3.2.1.2?cur為紅，f為紅，g為黑，u不存在/u存在且為黑

3.2.1.2.1 g、f、cur構成一條直線

3.2.1.2.2?g、f、cur構成一條折線

3.2.2 調整部分的代碼實現

3.3 紅黑樹的驗證

3.4 測試代碼

四、紅黑樹實現完整代碼

一、紅黑樹的概念

紅黑樹，是一種二叉搜索樹，但在每個結點上增加一個存儲位表示結點的顏色，可以是Red或Black。 通過對任何一條從根到葉子的路徑上各個結點著色方式的限制，紅黑樹確保沒有一條路 徑會比其他路徑長出倆倍，因而是接近平衡的。

二、紅黑樹的性質

● 每個結點不是紅色就是黑色

● 根節點是黑色的

● 如果一個節點是紅色的，則它的兩個孩子結點是黑色的（不允許出現連續的紅色節點）

● 對于每個結點，從該結點到其所有后代葉結點的簡單路徑上，均包含相同數目的黑色結點（從根節點到每個葉子節點的空孩子路徑上有相同數目的黑色節點）

● 每個葉子結點的空孩子節點都是黑色的

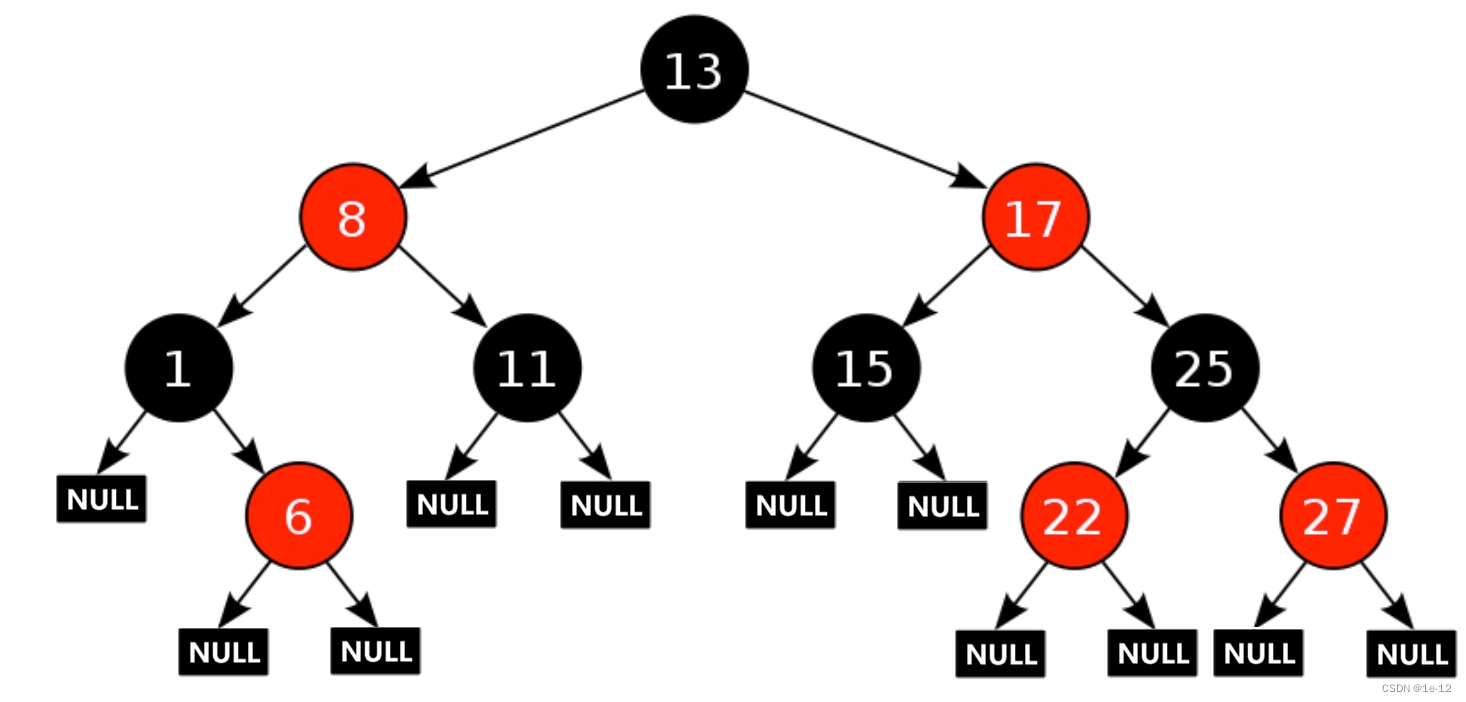
根據上述的五條性質，我們可以發現一個紅黑樹中如果有N個黑色節點，則根節點到任意一個葉子節點的距離：最短為㏒⑵N，最長為2㏒⑵N

2.1 紅黑樹與AVL樹的比較

我們來看到下面的紅黑樹：

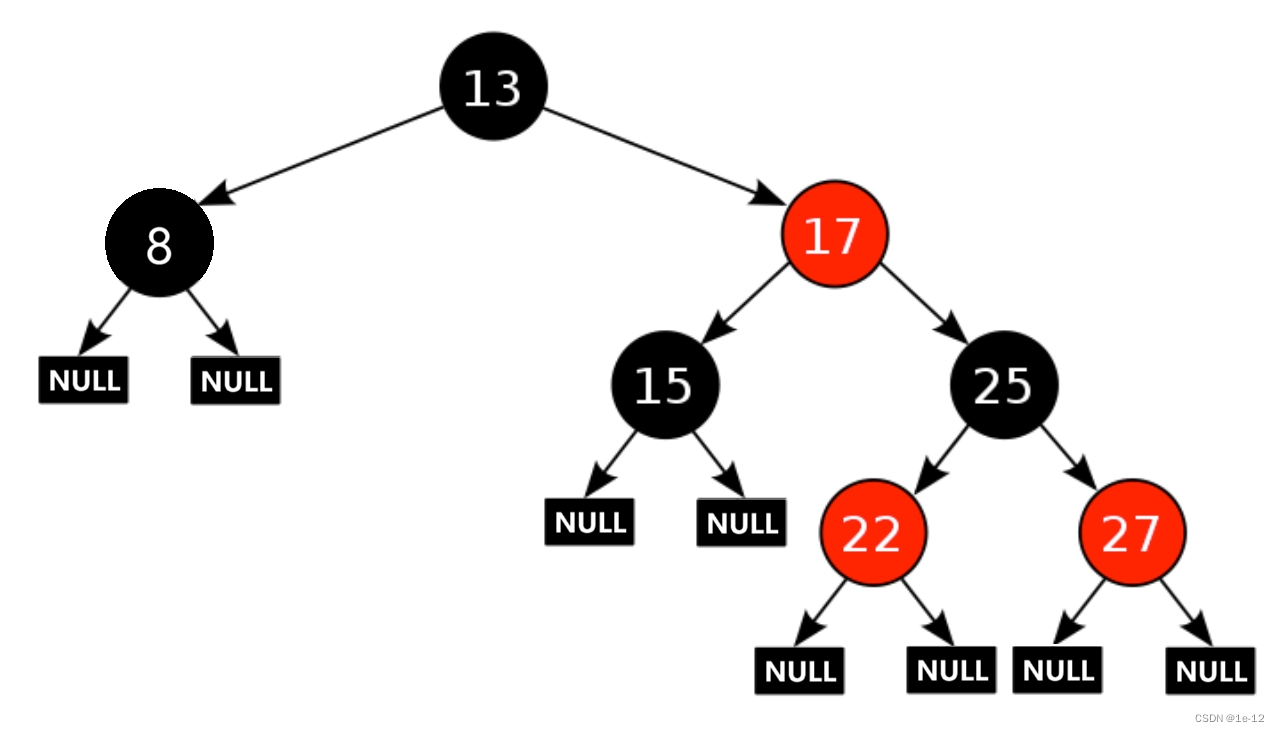
對于這棵紅黑樹，如果將其看成一個AVL樹，是需要進行旋轉的，但是在紅黑樹結構中卻不需要

所以紅黑樹是近似平衡的，在搜索效率上會略遜AVL樹一些，但是紅黑樹在結構上不要求絕對的平衡，這就造成插入相同的數據紅黑樹翻轉的次數少于AVL樹

實際使用中，在經常進行增刪的場景下紅黑樹性能比AVL樹更優，并且紅黑樹實現比較簡單，所以實際運用中紅黑樹更多

三、紅黑樹的實現

3.1 紅黑樹節點的定義

enum Colour
{RED,BLACK
};template<class Key, class Val>
struct RBTreeNode
{RBTreeNode<Key, Val>* _left;RBTreeNode<Key, Val>* _right;RBTreeNode<Key, Val>* _parent;//多一個指針指向其父節點,方便我們的后續操作pair<Key, Val> _kv;Colour _col;//顏色標識RBTreeNode(const pair<Key, Val>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED)//構造時,優先將節點的顏色置為紅色{}
};

在這里提一下為什么要默認將節點的顏色置為紅色：

在我們向紅黑樹中插入一個新節點時，如果將該節點置為黑色，就肯定會影響紅黑樹性質中的第四條：對于每個結點，從該結點到其所有后代葉結點的簡單路徑上，均包含相同數目的黑色結點

例如：

我們現在在上面這棵樹中，不管在哪個葉子節點的下方插入一個黑色的新增節點，從根節點到插入的節點的空孩子的路徑上的黑色節點數目會變為4，而從根節點到其他葉子節點的空孩子的路徑上的黑色節點數目會都為3

所以我們將新增節點的顏色置為紅色就一定不會違反第四條紅黑樹性質，但是第三條呢？如果插入節點的父節點是紅色的怎么辦？

怎么辦我們后面再說，反正總歸比置為黑色一定會違反第四條性質好吧

3.2 數據的插入

由于紅黑樹也是平衡二叉搜索樹的一種，我們在插入數據時也要找到合適的位置進行插入：

template<class Key, class Val>
class RBTree
{typedef RBTreeNode<Key, Val> Node;
public:bool Insert(const pair<Key,Val>& kv){Node* cur = _root, * parent = nullptr;while (cur)//找到合適的位置{if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{cout << "插入的值重復" << endl;return false;}}cur = new Node(kv);cur->_parent = parent;//將插入的節點連接上二叉樹if (parent == nullptr){_root = cur;}else if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}return true;}private:Node* _root = nullptr;
};

插入到合適的位置之后，我們還要檢查是否破壞了紅黑樹的結構（由于我們插入的是紅色節點，所以只會出現兩個紅色節點連續的情況），如果出現了該情況，我們就要對其進行分類討論并解決：

3.2.1 紅黑樹的調整思路

下面我們將出現異常情況的兩個節點的那個子節點叫做cur，cur的父節點叫做father（簡稱f），father的父節點叫做grandfather（簡稱g），father的兄弟節點叫做uncle（簡稱u）

例如：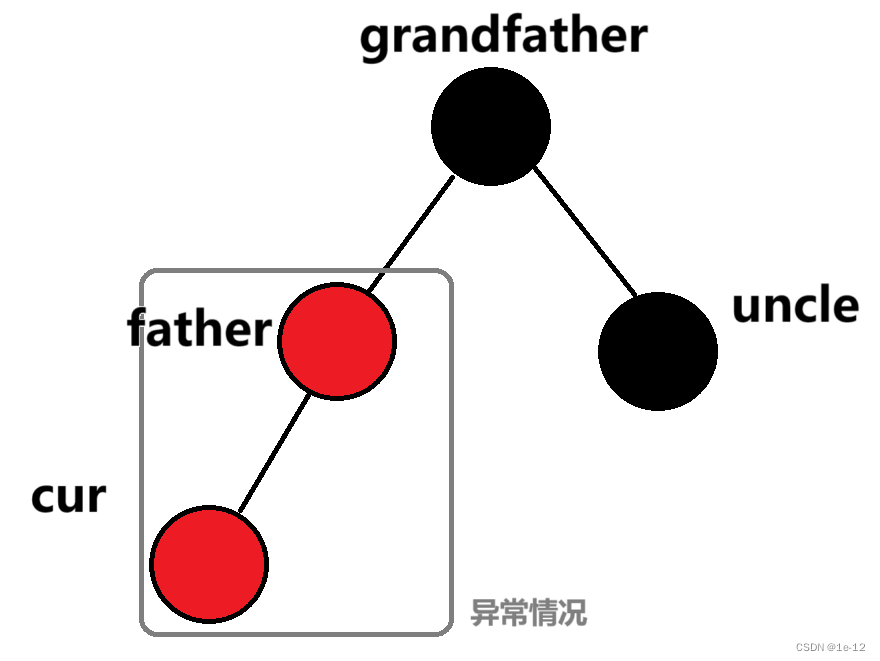

接下來，我們分類討論：

3.2.1.1?cur為紅，f為紅，g為黑，u存在且為紅

下面畫出的情況表示的是抽象出的情況：A、B、C、D、E都是滿足構成紅黑樹的子樹

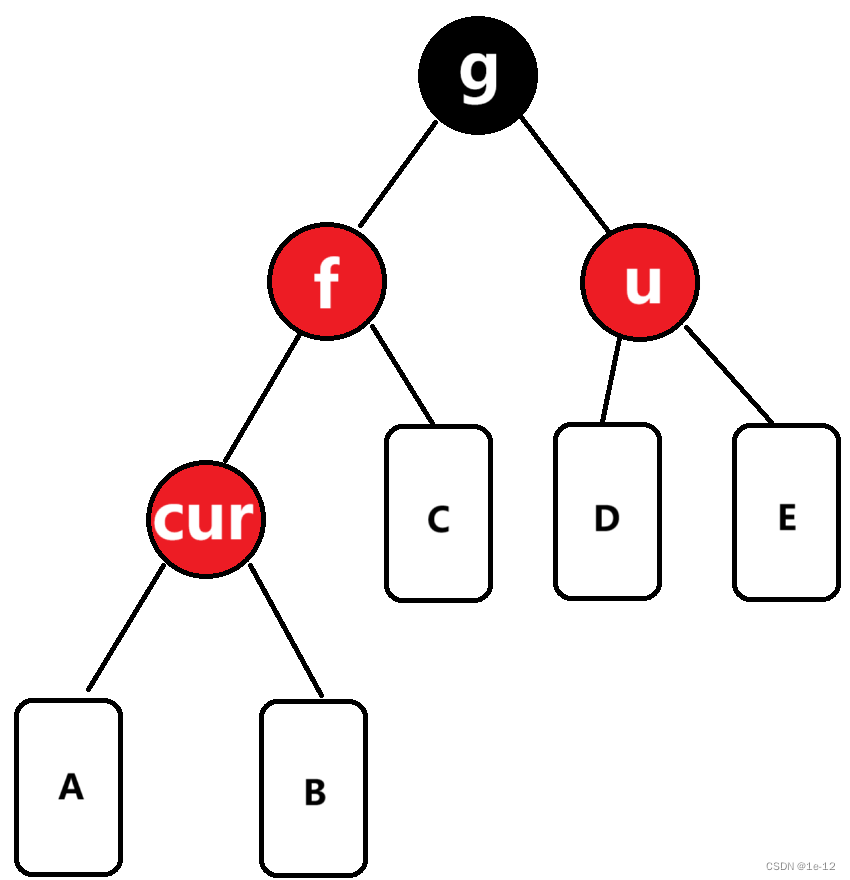
對于這種情況我們先將f和u節點變黑，再將g節點變紅即可：

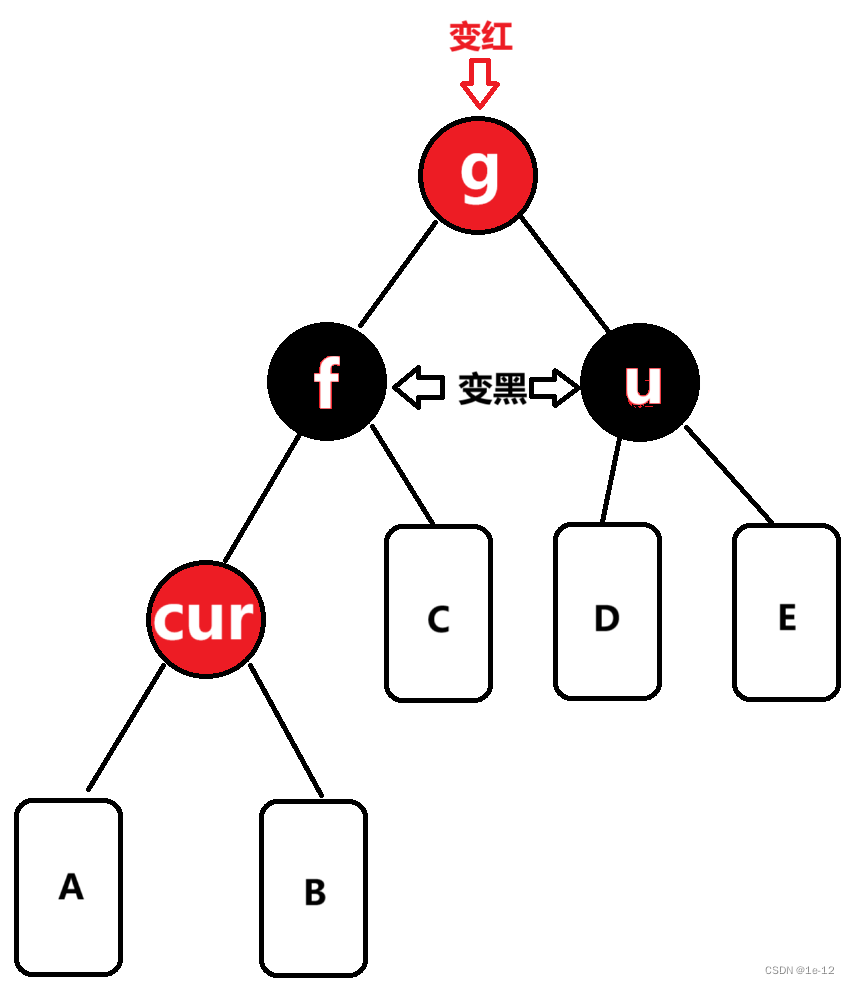
調整完后，要記得再向上檢查g節點的父節點是否為紅色哦~（如果g節點為整棵紅黑樹的根，最后要將其顏色置為黑）

3.2.1.2?cur為紅，f為紅，g為黑，u不存在/u存在且為黑
3.2.1.2.1 g、f、cur構成一條直線

對于這種情況：若f為g的左孩子，cur為f的左孩子，則進行右單旋：

再將f變黑，g變紅：

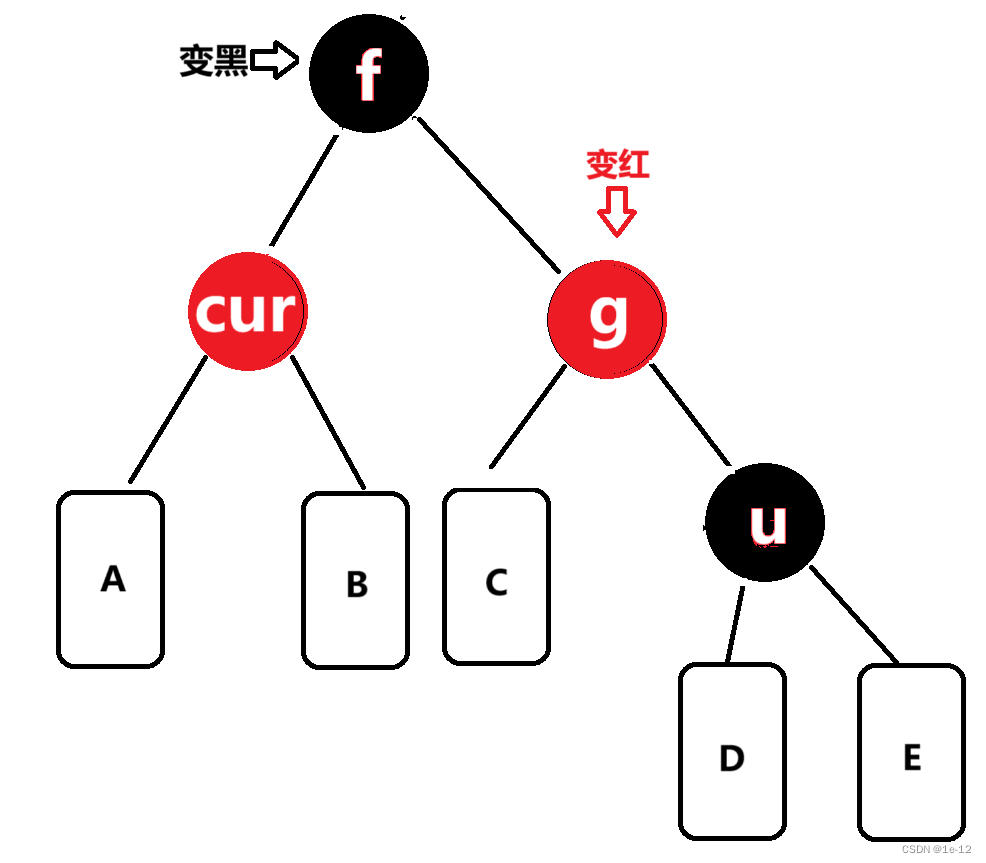
相反， f為g的右孩子，cur為f的右孩子，則進行左單旋轉：

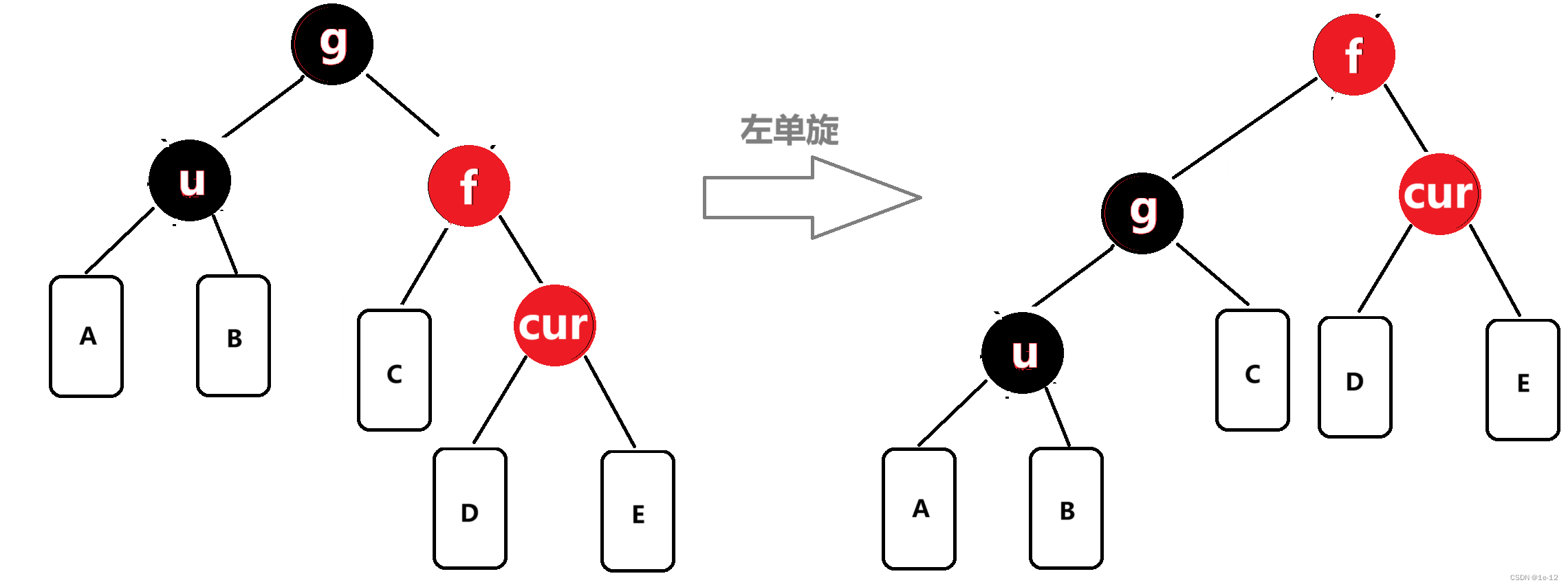
再將f變黑，g變紅：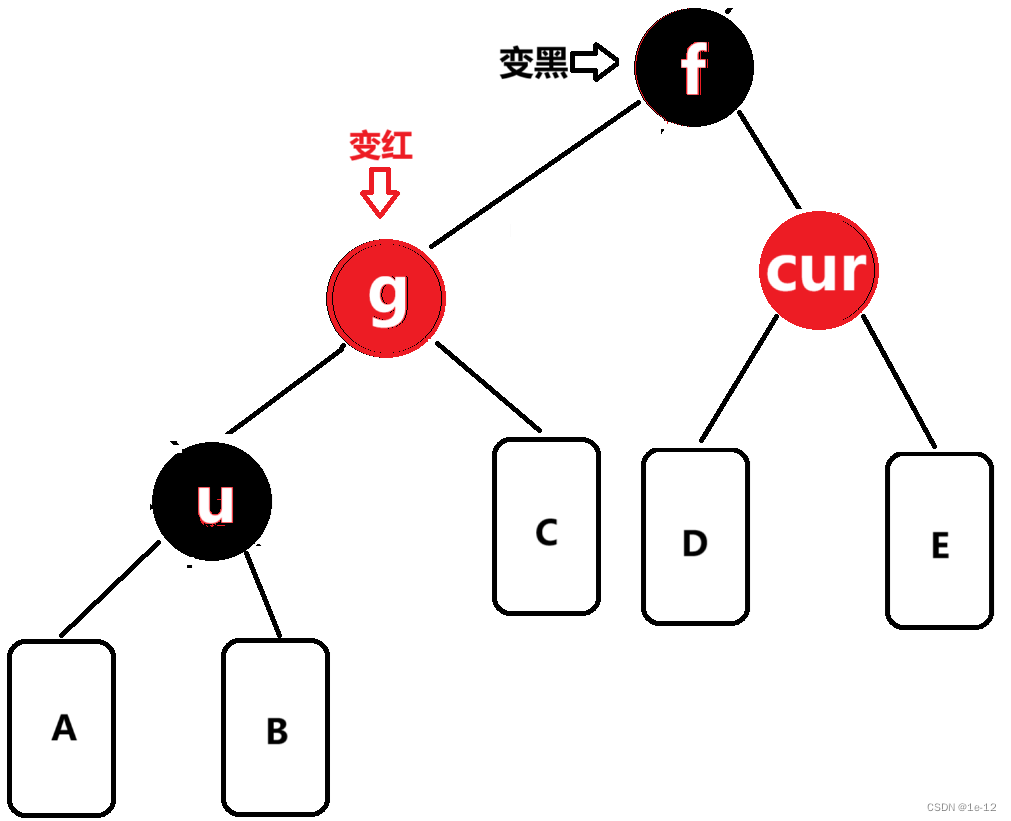

3.2.1.2.2?g、f、cur構成一條折線

f為g的左孩子，cur為f的右孩子，則做左右雙旋，旋轉完后將cur節點顏色置黑、g節點顏色置紅：

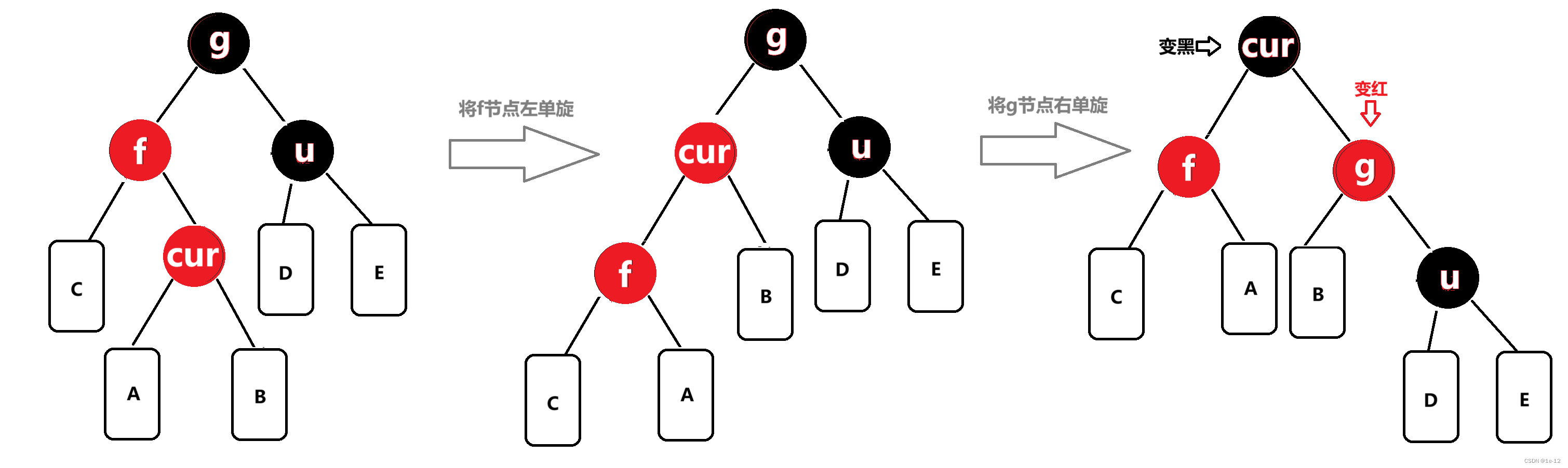
相反， f為g的右孩子，cur為f的左孩子，則做右左雙旋，旋轉完后將cur節點顏色置黑、g節點顏色置紅：

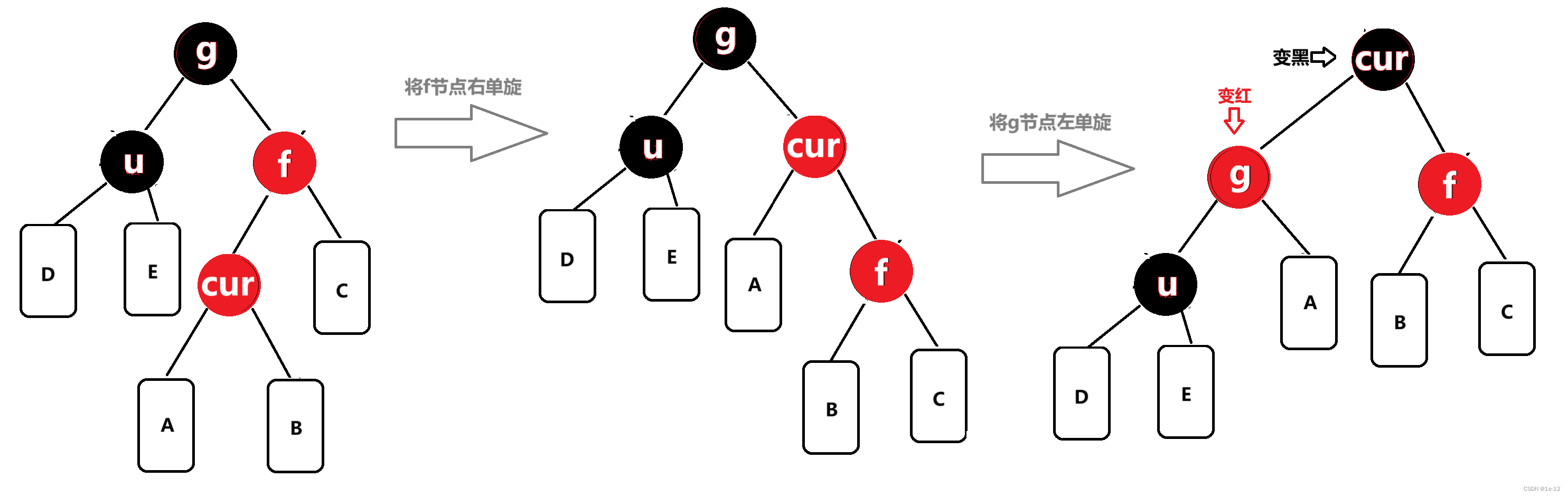
對于旋轉操作還不熟悉的同學可以看到這里：【數據結構高階】AVL樹

3.2.2 調整部分的代碼實現

template<class Key, class Val>
class RBTree
{typedef RBTreeNode<Key, Val> Node;
public:bool Insert(const pair<Key, Val>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root, * parent = nullptr;while (cur)//找到合適的位置{if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{cout << "插入的值重復" << endl;return false;}}cur = new Node(kv);//將插入的節點連接上二叉樹if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//開始調整while (parent && parent->_col == RED)//紅黑樹的結構出現兩個連續的紅色節點{Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED)//cur為紅，p為紅，g為黑，u存在且為紅{parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//繼續向上更新cur = grandfather;parent = cur->_parent;}elsecur為紅，p為紅，g為黑，u不存在/u存在且為黑{if (cur == parent->_left)//cur在p的左邊,p也在g的左邊，構成一條直線{//右單旋RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//cur在p的右邊,p在g的左邊，構成一條折線{//左右雙旋RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//調整完跳出}}else{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED)//cur為紅，p為紅，g為黑，u存在且為紅{parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//繼續向上更新cur = grandfather;parent = cur->_parent;}elsecur為紅，p為紅，g為黑，u不存在/u存在且為黑{if (cur == parent->_right)//cur在p的右邊,p也在g的右邊，構成一條直線{//左單旋RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//cur在p的左邊,p在g的右邊，構成一條折線{//右左雙旋RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//調整完跳出}}}_root->_col = BLACK;//確保即便進行過調整后根節點顏色為黑return true;
}private:void RotateL(Node* parent)//左單旋{Node* subR = parent->_right;Node* subRL = subR->_left;Node* pparent = parent->_parent;parent->_right = subRL;//更新parent的右節點if (subRL)//防止該節點為空{subRL->_parent = parent;//更新subRL的父節點}parent->_parent = subR;//更新parent的父節點subR->_left = parent;//subR的左子樹置為parentsubR->_parent = pparent;//更新subR的父節點if (pparent == nullptr)//旋轉的是整棵樹{_root = subR;//更新根節點}else//將旋轉后的子樹鏈接上整個二叉樹{if (pparent->_left == parent){pparent->_left = subR;}else{pparent->_right = subR;}}}void RotateR(Node* parent)//右單旋{Node* subL = parent->_left;Node* subLR = subL->_right;Node* pparent = parent->_parent;parent->_left = subLR;//更新parent的左節點if (subLR)//防止該節點為空{subLR->_parent = parent;//更新subLR的父節點}parent->_parent = subL;//更新parent的父節點subL->_right = parent;//subL的右子樹置為parentsubL->_parent = pparent;//更新subL的父節點if (pparent == nullptr)//旋轉的是整棵樹{_root = subL;//更新根節點}else//將旋轉后的子樹鏈接上整個二叉樹{if (pparent->_left == parent){pparent->_left = subL;}else{pparent->_right = subL;}}}private:Node* _root = nullptr;
};

3.3 紅黑樹的驗證

下面我們來寫段代碼來驗證一課樹是不是紅黑樹：

template<class Key, class Val>
class RBTree
{typedef RBTreeNode<Key, Val> Node;
public:bool IsBalance(){if (_root && _root->_col == RED){cout << "根節點顏色是紅色" << endl;return false;}int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)++benchmark;cur = cur->_left;}// 連續紅色節點return _Check(_root, 0, benchmark);}private:bool _Check(Node* root, int blackNum, int benchmark)//計算每條路徑上黑色節點的個數{if (root == nullptr){if (benchmark != blackNum){cout << "某條路徑黑色節點的數量不相等" << endl;return false;}return true;}if (root->_col == BLACK){++blackNum;}if (root->_col == RED&& root->_parent&& root->_parent->_col == RED){cout << "存在連續的紅色節點" << endl;return false;}return _Check(root->_left, blackNum, benchmark)&& _Check(root->_right, blackNum, benchmark);}private:Node* _root = nullptr;
};

3.4 測試代碼

void Test_RBTree()
{const size_t N = 50000;RBTree<int, int> t;for (size_t i = 0; i < N; ++i){size_t x = rand() + i;t.Insert(make_pair(x, x));}t.InOrder();cout << t.IsBalance();
}int main()
{Test_RBTree();return 0;
}

測試效果：

四、紅黑樹實現完整代碼

#include<iostream>using namespace std;enum Colour
{RED,BLACK
};template<class Key, class Val>
struct RBTreeNode
{RBTreeNode<Key, Val>* _left;RBTreeNode<Key, Val>* _right;RBTreeNode<Key, Val>* _parent;//多一個指針指向其父節點,方便我們的后續操作pair<Key, Val> _kv;Colour _col;//顏色標識RBTreeNode(const pair<Key, Val>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED)//默認構造時,優先將節點的顏色置為紅色{}
};template<class Key, class Val>
class RBTree
{typedef RBTreeNode<Key, Val> Node;
public:bool Insert(const pair<Key, Val>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root, * parent = nullptr;while (cur)//找到合適的位置{if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{cout << "插入的值重復" << endl;return false;}}cur = new Node(kv);//將插入的節點連接上二叉樹if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//開始調整while (parent && parent->_col == RED)//紅黑樹的結構出現兩個連續的紅色節點{Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;if (uncle && uncle->_col == RED)//cur為紅，p為紅，g為黑，u存在且為紅{parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//繼續向上更新cur = grandfather;parent = cur->_parent;}elsecur為紅，p為紅，g為黑，u不存在/u存在且為黑{if (cur == parent->_left)//cur在p的左邊,p也在g的左邊，構成一條直線{//右單旋RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//cur在p的右邊,p在g的左邊，構成一條折線{//左右雙旋RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//調整完跳出}}else{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED)//cur為紅，p為紅，g為黑，u存在且為紅{parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;//繼續向上更新cur = grandfather;parent = cur->_parent;}elsecur為紅，p為紅，g為黑，u不存在/u存在且為黑{if (cur == parent->_right)//cur在p的右邊,p也在g的右邊，構成一條直線{//左單旋RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//cur在p的左邊,p在g的右邊，構成一條折線{//右左雙旋RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//調整完跳出}}}_root->_col = BLACK;//確保即便進行過調整后根節點顏色為黑return true;
}void InOrder()//中序遍歷{_InOrder(_root);cout << endl;}bool IsBalance(){if (_root && _root->_col == RED){cout << "根節點顏色是紅色" << endl;return false;}int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)++benchmark;cur = cur->_left;}// 連續紅色節點return _Check(_root, 0, benchmark);}private:void RotateL(Node* parent)//左單旋{Node* subR = parent->_right;Node* subRL = subR->_left;Node* pparent = parent->_parent;parent->_right = subRL;//更新parent的右節點if (subRL)//防止該節點為空{subRL->_parent = parent;//更新subRL的父節點}parent->_parent = subR;//更新parent的父節點subR->_left = parent;//subR的左子樹置為parentsubR->_parent = pparent;//更新subR的父節點if (pparent == nullptr)//旋轉的是整棵樹{_root = subR;//更新根節點}else//將旋轉后的子樹鏈接上整個二叉樹{if (pparent->_left == parent){pparent->_left = subR;}else{pparent->_right = subR;}}}void RotateR(Node* parent)//右單旋{Node* subL = parent->_left;Node* subLR = subL->_right;Node* pparent = parent->_parent;parent->_left = subLR;//更新parent的左節點if (subLR)//防止該節點為空{subLR->_parent = parent;//更新subLR的父節點}parent->_parent = subL;//更新parent的父節點subL->_right = parent;//subL的右子樹置為parentsubL->_parent = pparent;//更新subL的父節點if (pparent == nullptr)//旋轉的是整棵樹{_root = subL;//更新根節點}else//將旋轉后的子樹鏈接上整個二叉樹{if (pparent->_left == parent){pparent->_left = subL;}else{pparent->_right = subL;}}}void _InOrder(Node* root){if (root == NULL)//如果是空樹就直接結束{return;}_InOrder(root->_left);//先遞歸遍歷其左子樹cout << root->_kv.first << " ";//再遍歷其根節點_InOrder(root->_right);//最后遞歸遍歷其右子樹}bool _Check(Node* root, int blackNum, int benchmark){if (root == nullptr){if (benchmark != blackNum){cout << "某條路徑黑色節點的數量不相等" << endl;return false;}return true;}if (root->_col == BLACK){++blackNum;}if (root->_col == RED&& root->_parent&& root->_parent->_col == RED){cout << "存在連續的紅色節點" << endl;return false;}return _Check(root->_left, blackNum, benchmark)&& _Check(root->_right, blackNum, benchmark);}private:Node* _root = nullptr;
};

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/212951.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/212951.shtml
英文地址，請注明出處：http://en.pswp.cn/news/212951.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

【重點】【LCA】236. 二叉樹的最近公共祖先

【重點】【LCA】236. 二叉樹的最近公共祖先

題目 class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if (root null || root p || root q) {return root;}TreeNode left lowestCommonAncestor(root.left, p, q);TreeNode right lowestCommonAncestor(root.right, p, …
閱讀更多...
【重點】【DFS】124.二叉樹中的最大路徑和

【重點】【DFS】124.二叉樹中的最大路徑和

題目 和求二叉樹直徑相同套路 class Solution {private int max Integer.MIN_VALUE;public int maxPathSum(TreeNode root) {if (root null) {return 0;}dfs(root);return max;}// 返回經過root的單邊分支最大和public int dfs(TreeNode root) {if (root null) {return 0;}…
閱讀更多...
IT新聞資訊系統，使用mysql作為后臺數據庫，此系統具有顯示數據庫中的所有信息和刪除兩大功能。

IT新聞資訊系統，使用mysql作為后臺數據庫，此系統具有顯示數據庫中的所有信息和刪除兩大功能。

表的準備&#xff1a; -- MySQL Administrator dump 1.4 -- -- ------------------------------------------------------ -- Server version 5.1.40-community /*!40101 SET OLD_CHARACTER_SET_CLIENTCHARACTER_SET_CLIENT */; /*!40101 SET OLD_CHARACTER_SET_RESULTSCHAR…
閱讀更多...
LTP測試

LTP測試

LTP 測試 LTP套件是由 Linux Test Project 所開發的一套系統測試套件。它基于系統資源的利用率統計開發了一個測試的組合,為系統提供足夠的壓力。通過壓力測試來判斷系統的穩定性和可靠性。壓力測試是一種破壞性的測試,即系統在非正常的、超負荷的條件下的運行情況 。用來評估…
閱讀更多...
mysql庫名規范

mysql庫名規范

mysql庫名的一些規范和建議&#xff1a; 庫名以小寫字母、數字、下劃線組成&#xff0c;不要以數字開頭。建議不要超過32個字符&#xff0c;但盡量用簡短的名稱。因為很多地方用到庫名&#xff0c;如果庫名太長&#xff0c;容易出錯。庫名選擇有意義的名稱&#xff0c;盡量與應…
閱讀更多...
55.手寫實現grpc連接池以及gin和grpc交互

55.手寫實現grpc連接池以及gin和grpc交互

文章目錄 一、簡介前置說明 二、敏感詞過濾服務1、定義sensitive.proto文件2、protoc生成pb.go文件3、sensitive服務端實現 三、關鍵詞匹配服務1、編寫keywords.proto文件2、生成pb.go文件3、keywords服務端實現 四、gin web 路由服務1、新建grpcpool服務作為gin web服務2、根據…
閱讀更多...
GEE影像升尺度（10m-＞250m）

GEE影像升尺度（10m-＞250m）

GEE影像升尺度&#xff08;10m->250m&#xff09; 代碼 var ext /* color: #d63000 *//* shown: false *//* displayProperties: [{"type": "rectangle"}] */ee.Geometry.Polygon([[[108.74625980473367, 28.562445155322063],[108.74625980473367, …
閱讀更多...
【MySQL】之死鎖問題及其解決方案

【MySQL】之死鎖問題及其解決方案

前言 數據庫死鎖問題是我們老生常談的問題了&#xff0c;在我們實際開發過程中經常會遇到&#xff0c;為了盡量避免出現死鎖&#xff0c;我們需要了解出現死鎖的場景。同時&#xff0c;如果線上出現了死鎖之后怎么去分析、排查和解決&#xff0c;下面我就這兩點介紹一下。 一、…
閱讀更多...
ubuntu22.04 怎么開啟SSH服務

ubuntu22.04 怎么開啟SSH服務

在 Ubuntu 22.04 LTS 中&#xff0c;默認情況下不會自動啟動 SSH 服務。如果你想通過 SSH 訪問你的 Ubuntu 系統&#xff0c;你需要手動安裝 SSH 服務器&#xff0c;并確保 22 端口&#xff08;SSH 的默認端口&#xff09;是開放的。以下是必要的步驟&#xff1a; 安裝 SSH 服…
閱讀更多...
Java 多線程之同步（鎖）相關類總結

Java 多線程之同步（鎖）相關類總結

文章目錄 一、概述二、volatile 可見性/有序性三、synchronized 互拆鎖/排他鎖/非觀鎖四、DCL&#xff08;Double-Checked Locking&#xff09;五、CAS&#xff08;Compare and Set&#xff09;六、ReentrantLock 可重入鎖/公平/非公平鎖七、ReentrantReadWriteLock 讀寫鎖/共享…
閱讀更多...
Day56力扣打卡

Day56力扣打卡

打卡記錄 數對統計&#xff08;DP狀態壓縮&#xff09; 參考文獻 #include <bits/stdc.h>using namespace std;void solve(){int n;cin >> n;map<int, int> mapp;vector<int> a(n);for (auto& x : a){cin >> x;mapp[x] ;}vector<array&…
閱讀更多...
使用WebyogSQLyog使用數據庫

使用WebyogSQLyog使用數據庫

數據庫 實現數據持久化到本地&#xff1a; 使用完整的管理系統統一管理&#xff0c; 數據庫&#xff08;DateBase&#xff09;&#xff1a; 為了方便數據存儲和管理&#xff08;增刪改查&#xff09;&#xff0c;將數據按照特定的規則存儲起來 安裝WebyogSQLyog -- 創建數…
閱讀更多...
101基于matlab的極限學習機ELM算法進行遙感圖像分類

101基于matlab的極限學習機ELM算法進行遙感圖像分類

基于matlab的極限學習機ELM算法進行遙感圖像分類&#xff0c;對所獲取的遙感圖片進行初步分類和最終分類。數據可更換自己的&#xff0c;程序已調通&#xff0c;可直接運行。
閱讀更多...
如何使用 Explain 分析 SQL 語句？

如何使用 Explain 分析 SQL 語句？

如何使用 Explain 分析 SQL 語句&#xff1f; MySQL中EXPLAIN命令是我們分析和優化SQL語句的利器。 如何使用EXPLAIN來分析SQL語句&#xff0c;接下來有15個例子&#xff0c;一起學習唄 1. EXPLAIN的基本使用 EXPLAIN可以用于分析MySQL如何執行一個SQL查詢&#xff0c;包括如…
閱讀更多...
ElasticSearch之cat repositories API

ElasticSearch之cat repositories API

命令樣例如下&#xff1a; curl -X GET "https://localhost:9200/_cat/repositories?vtrue&pretty" --cacert $ES_HOME/config/certs/http_ca.crt -u "elastic:ohCxPHQBEs5*lo7F9"執行結果輸出如下&#xff1a; id type repo1 fs repo2 s3查…
閱讀更多...
python+gdal地理坐標轉投影坐標

python+gdal地理坐標轉投影坐標

1 前言 地理坐標系&#xff0c;是使用三維球面來定義地球表面位置&#xff0c;以實現通過經緯度對地球表面點位引用的坐標系。 地理坐標系經過地圖投影操作后就變成了投影坐標系。而地圖投影是按照一定的數學法則將地球橢球面上點的經維度坐標轉換到平面上的直角坐標。 2 流程…
閱讀更多...
基于STM32的四位數碼管計數器設計與實現

基于STM32的四位數碼管計數器設計與實現

?作者簡介&#xff1a;熱愛科研的嵌入式開發者&#xff0c;修心和技術同步精進&#xff0c; 代碼獲取、問題探討及文章轉載可私信。 ? 愿你的生命中有夠多的云翳,來造就一個美麗的黃昏。 &#x1f34e;獲取更多嵌入式資料可點擊鏈接進群領取&#xff0c;謝謝支持&#xff01;…
閱讀更多...
Docker Compose(容器編排)——9

Docker Compose(容器編排)——9

目錄 什么是 Docker Compose生活案例為什么要 Docker ComposeDocker Compose 的安裝Docker Compose 的功能Docker Compose 使用場景Docker Compose 文件&#xff08;docker-compose.yml&#xff09; 文件語法版本文件基本結構及常見指令Docker Compose 命令清單 命令清單如下命…
閱讀更多...
垃圾回收器CMS和G1的區別

垃圾回收器CMS和G1的區別

CMS和G1的區別 區別一&#xff1a; 使用范圍不一樣 CMS收集器是老年代的收集器&#xff0c;可以配合新生代的Serial和ParNew收集器一起使用 G1收集器收集范圍是老年代和新生代。不需要結合其他收集器使用 區別二&#xff1a; STW的時間 CMS收集器以最小的停頓時間為目標的收…
閱讀更多...
C++11(下)

C++11(下)

可變參數模板 C11的新特性可變參數模板能夠創建可以接受可變參數的函數模板和類模板. 相比C98/03, 類模版和函數模版中只能含固定數量的模版參數, 可變模版參數無疑是一個巨大的改進, 然而由于可變模版參數比較抽象, 使用起來需要一定的技巧, 所以這塊還是比較晦澀的.掌握一些基…
閱讀更多...
最新文章

Copyright @ 2022~2023