一、定義

1、任務

根據語法規則（即語言的文法），分析并識別出各種語法成分，如表達式、各種說明、各種語句、過程、函數等，并進行語法正確性檢查

2、對比

詞法分析：3型（正則文法） 詞法分析：字符串
語法分析：2型（上下文無關文法） 語法分析：符號串

3、方法

1. 自頂向下（Top-Down）分析：推導（Derivations）
   若$Z={>}^{+}S則S\in L(G[Z])否則S\notin L(G[Z])$
2. 自底向上（Bottom-Up）分析：規約（Reductions）
   若$Z<{=}^{+}S則S\in L(G[Z])否則S\notin L(G[Z])$

本節主要分析自頂向下方法

4、自頂向下面臨問題

推導順序：有多個“非終結符”，優先用哪個？
避免二義性：避免文法有多個可用規則。

問題：左遞歸問題+回溯問題
常見方法：遞歸子程序法+LL分析法

二、自頂向下分析

1、概念

給定符號串S，若預測是某一語法成分，則可根據該語法成分的文法,設法為S構造一棵語法樹，若成功,則S最終被識別為某一語法成分,即$S\in L(G[Z])$，其中G[Z]為某語法成分的文法。若不成功, 則 $S\notin L(G[Z])$

2、特點

1. 分析過程是帶預測的，對輸入符號串要預測屬于什么語法成分，然后根據該語法成分的文法建立語法樹。
2. 分析過程是一種試探過程，是盡一切辦法(選用不同規則) 來建立語法樹的過程, 由于是試探過程, 難免有失敗, 所以分析過程需進行回溯, 因此也稱這種方法是帶回溯的自頂向下分析方法。
3. 最左推導可以編寫程序來實現, 但帶溯的自頂向下分析方法在實際上價值不大, 效率低。

3、二義性問題

若對于一個文法的某一句子（或句型）存在兩棵不同的語法樹，則該文法是二義性文法，否則是無二義性文法。

若一個文法的某句子存在兩個不同的規范推導，則該文法是二義性的，否則是無二義性的。

若一個文法的某規范句型的句柄不唯一，則該文法是二義性的，否則是無二義性的。

PS：正則文法也會有二義性，但是可判定的（通過轉換為自動機）

文法的二義性是不可判定的，因此解決方法是提出一些限制條件，稱為無二義性的充分條件，當文法滿足這些條件時，就可以判定文法是無二義性的。

4、左遞歸問題

1）概念

令U是文法的任一非終結符，文法中有規則$U::=U????或者U=>U???$

自頂向下分析的基本缺點是：不能處理具有左遞歸性的文法。
（如果在匹配輸入串的過程中，假定正好輪到要用非終結符U直接匹配輸入串，即要用U的右部符號串U¨¨去匹配，為了用U¨¨去匹配，又得用U去匹配，這樣無限的循環下
去將無法終止。）

2）消除

1. 使用擴充的BNF表示來改寫文法
   (1)$E::=E+T|T=>E::=T${$+T$}
   (2) $T::=T?F|T/F|F=>T::=F${$?F|/F$}

具體規則：
提因子：若：$U::=xy|xw|\dots .|xz則可改寫為：U::=x(y|w|\dots .|z)$

若有文法規則：$U::=x|y|\dots \dots |z|Uv可以改寫為U::=(x|y|\dots \dots |z)${$v$}
其特點是：具有一個直接左遞歸的右部并位于最后，這表明該語法類U是由x或y……或z其后隨有零個或多個v組成。
通過以上兩條規則，就能消除文法的直接左遞歸，并保持文法的等價性。

2. 將左遞歸規則改為右遞歸規則
   若：$P::=Pa|b$ 則可改寫為：$P::=bP’P’::=aP’|\epsilon$
   

3）間接左遞歸

此時需要代入成直接左遞歸后再處理

1. 檢查規則R是否存在直接左遞歸 $R::=Sa|a$
2. 把R代入Q的有關選擇，改寫規則Q $Q::=Sab|ab|b$
3. 檢查Q是否存在直接左遞歸
4. 把Q代入S的右部選擇 $S::=Sabc|abc|bc|c$
5. 消除S的直接左遞歸 $S::=(abc|bc|c)${$abc$}

5、回溯問題

1）概念

概念：分析工作要部分地或全部地退回去。

造成回溯的條件：文法中，對于某個非終結符號的規則其右部有多個選擇，并根據所面臨的輸入符號不能準確地確定所要的選擇時，就可能出現回溯。

2）消除

對于$U::={\alpha }_1|{\alpha }_2|{\alpha }_3$
定義：$FIRST({\alpha }_i)=${$a|{\alpha }_i={>}^{?}a\dots ,a\in V_t$}
為了避免回溯，對文法的要求是：$FIRST({\alpha }_i)\cap FIRST({\alpha }_j)=\phi (i\ne j)$

3）解決方法

1. 改寫文法
   判斷后若有相交，則需要把相交的部分提出放到高一級的文法中，如下例子：
   
2. 超前掃描（偷看）
   當文法不滿足避免回溯的條件時，即各選擇的首符號相交時，可以采用超前掃描的方法，即向前偵察各輸入符號串的第二個、第三個符號來確定要選擇的目標。

這種方法是通過向前多看幾個符號來確定所選擇的目標，從本質上來講也有回溯的味道，因此比第一種方法費時，但是假讀僅僅是向前偵察情況，不作任何語義處理工作

6、總結

為了在不采取超前掃描的前提下實現不帶回溯的自頂向下分析，文法需要滿足兩個條件：

1. 文法是非左遞歸的
2. 對文法的任一非終結符，若其規則右部有多個選擇時， 各選擇所推出的終結符號串的首符號集合要兩兩不相交。

在上述條件下，就可以根據文法構造有效的、不帶回溯的自頂向下分析器。

對于第二點，我們只有$FIRST$集合是不夠的：
定義$FOLLOW(A)=${$a|Z={>}^{?}\dots Aa\dots ，a\in V_t$}
$A\in V_n$ 該集合稱為A的后繼符號集合
特殊地：$若Z={>}^{?}...A$ 則 # $\in FOLLOW(A)$

不帶回溯的充分必要條件是：對于G的
每一個非終結符A的任意兩條規則$A::=\alpha |\beta$,下列條件成立：

1. $FIRST(\alpha )\cap FIRST(\beta )=Ф$
2. $若\beta =={>}^{?}\epsilon ,則FIRST(\alpha )\cap FOLLOW(A)=Ф$

三、遞歸子程序法（遞歸下降分析法）

1、概念

具體做法：對語法的每一個非終結符都編一個分析程序，當根據文法和當時的輸入符號預測到要用某個非終結符去匹配輸入串時，就調用該非終結符的分析程序

2、具體做法

1. 檢查并改寫文法
   
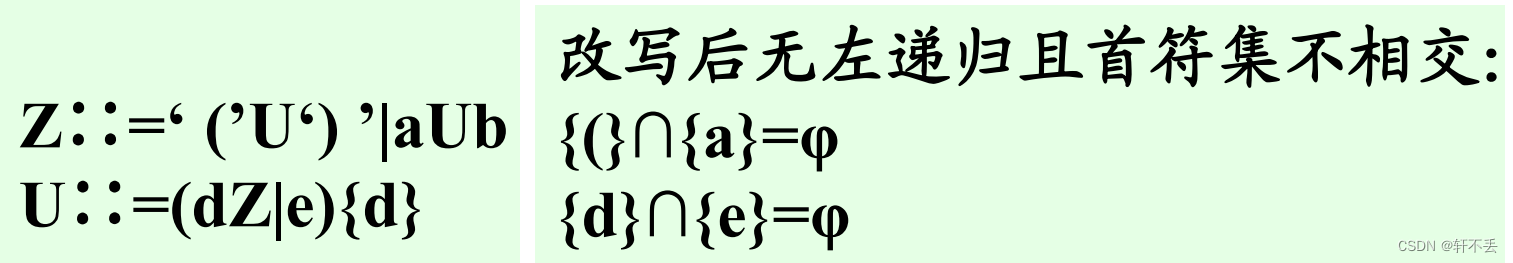
2. 檢查文法的遞歸性
   
   因此，Z和U的分析程序要編成遞歸子程序
3. 算法框圖
   非終結符號的分析子程序的功能是：用規則右部符號串去匹配輸入串
   
   

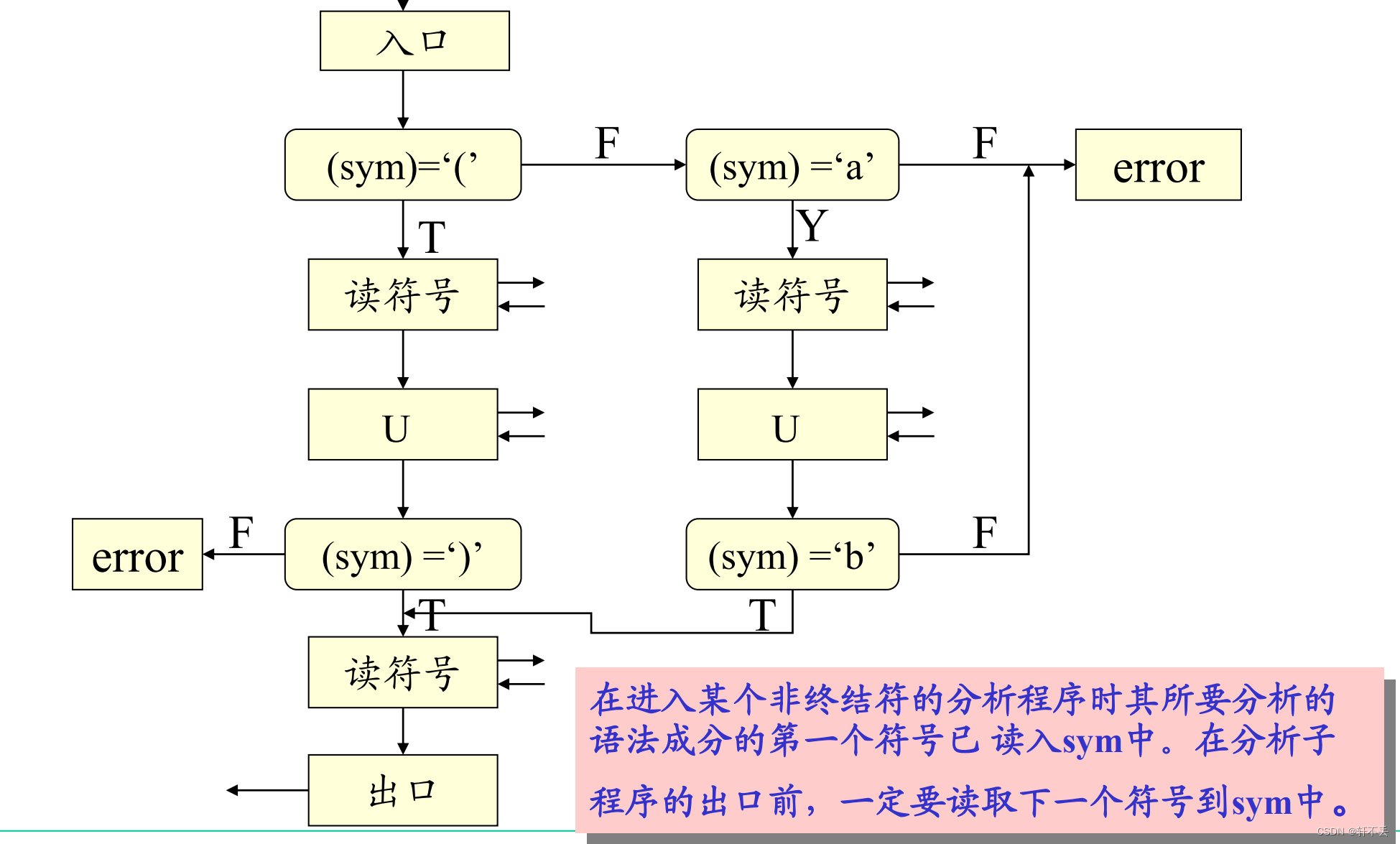
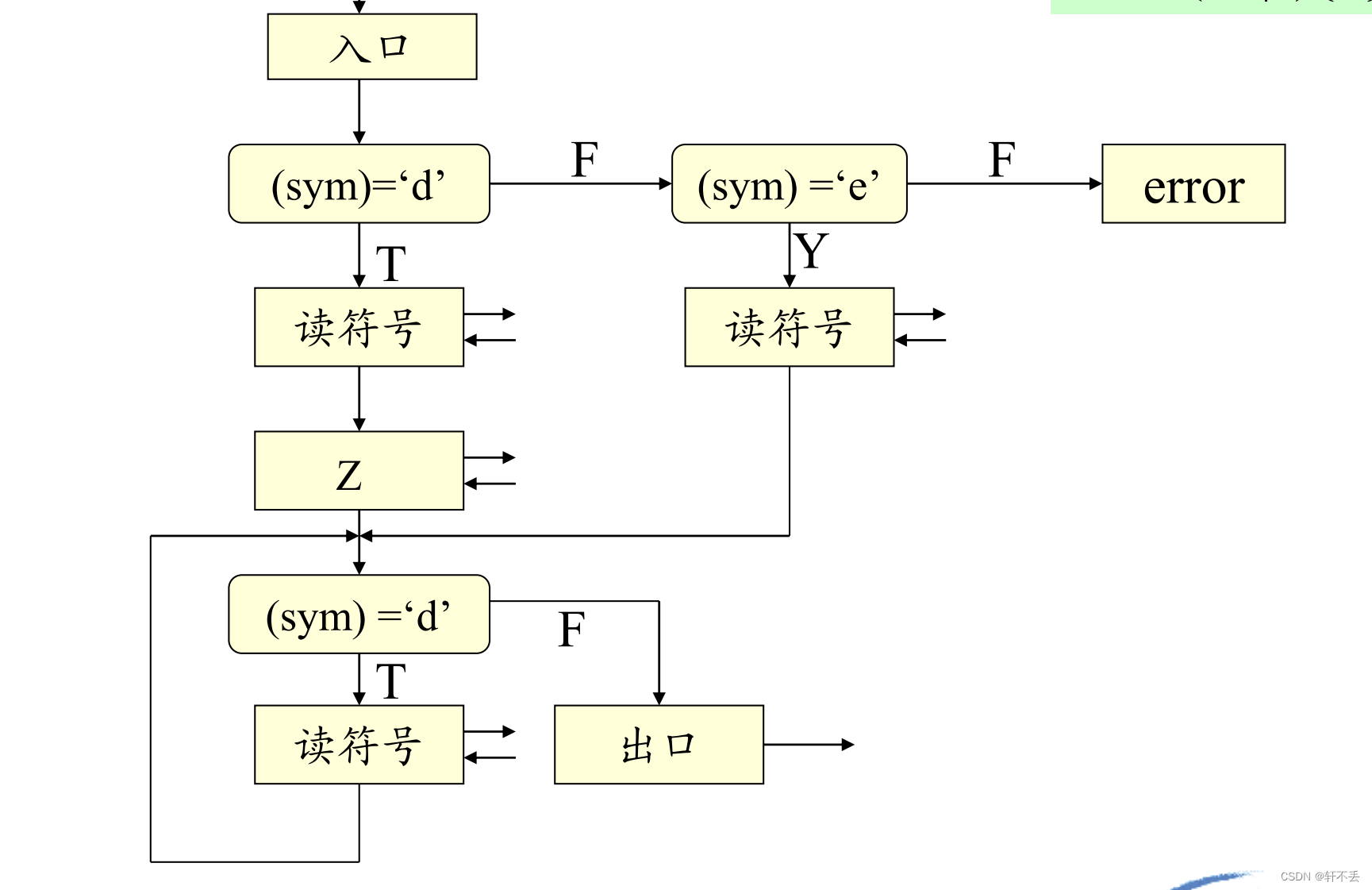
要注意子程序之間的接口,在程序編制時進入某個非終結符的分析程序時其所要分析的語法成分的第一個符號已讀入sym中。

遞歸子程序法對應的是最左推導過程

四、LL(1)文法

1、預備知識

1）FIRST集的計算

$FIRST({\alpha }_i)=${$a|{\alpha }_i={>}^{?}a\dots ,a\in V_t$}
若$\alpha ={>}^{?}\epsilon ，則\epsilon \in FIRST(\alpha )$

設$\alpha =X_1{X}_2...X_n,X_i\in V_{n}U{V}_t（即X_i\in V)$
首先求出組成α的每一個符號$X_i$的FIRST集合


注意：要順序往下做，一旦不滿足條件，過程就要中斷進行
得到$FIRST(X_i)，即可求出FIRST(\alpha )$

2）FOLLOW的算法

算法：連續使用以下規則，直至FOLLOW集合不再擴大

2、LL(1)文法的概念

第一個L：從左向右分析 (Left to right)
第二個L：產生“最左推導”(Left-most derivation)
k=1：向前查看“k=1”個符號，通過向前看1個符號就能夠有效分析
無二義，無左遞歸，且能夠消除回溯
因此判斷LL(1)文法的條件就是為了在不采取超前掃描的前提下實現不帶回溯的自頂向下分析所滿足的條件
無左遞歸且

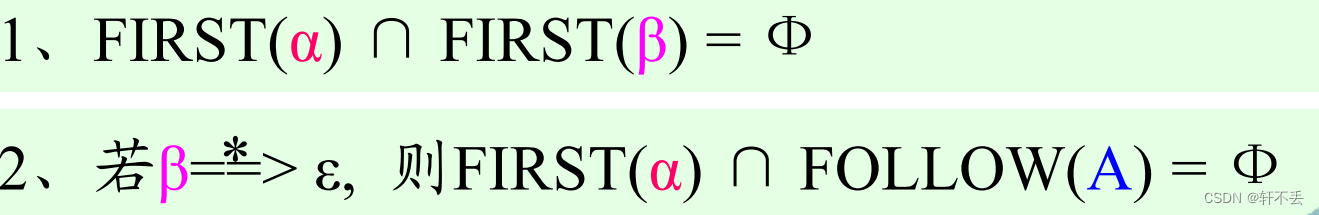
3、分析

1）組成

由三部分組成

1. 分析表
2. 執行程序 (總控程序）
3. 符號棧 （分析棧）
   
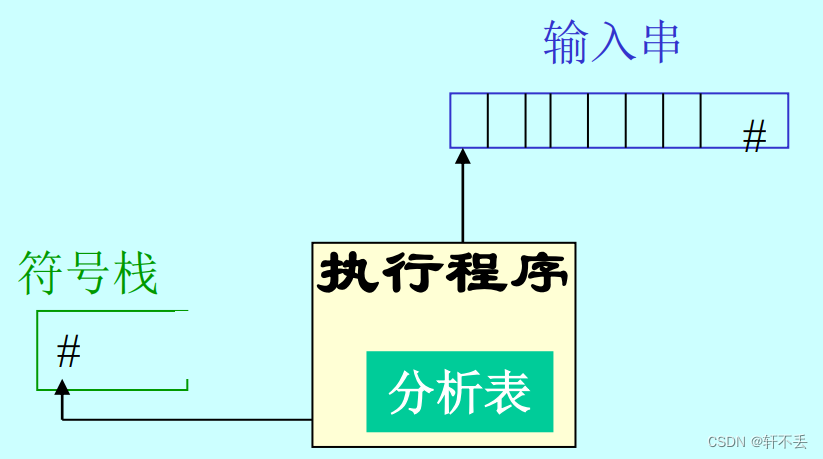
   在實際語言中，每一種語法成分都有確定的左右界符，為了研究問題方便，統一以‘＃’表示。

2）分析表

算法：

3）符號棧

四種狀態

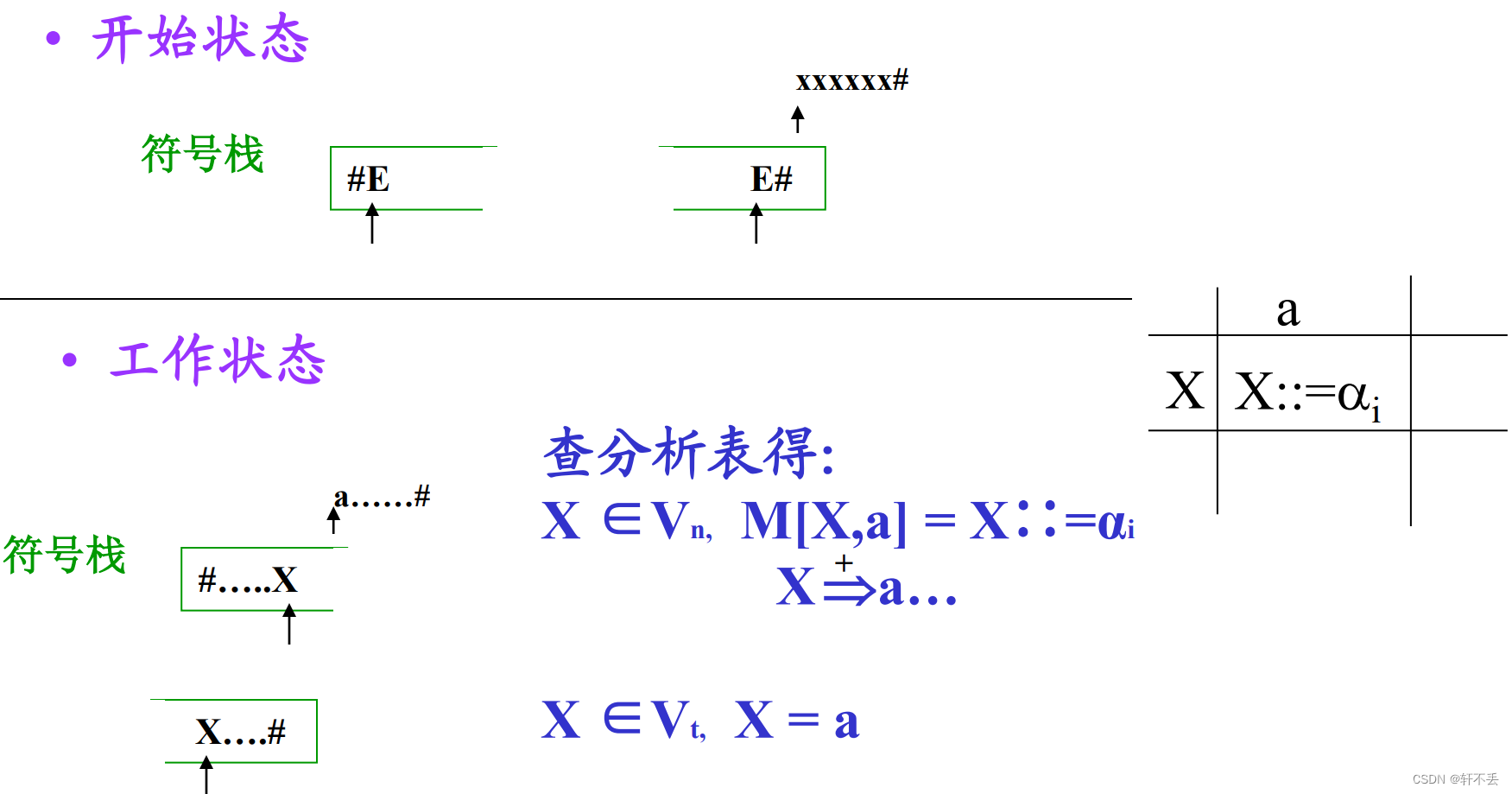
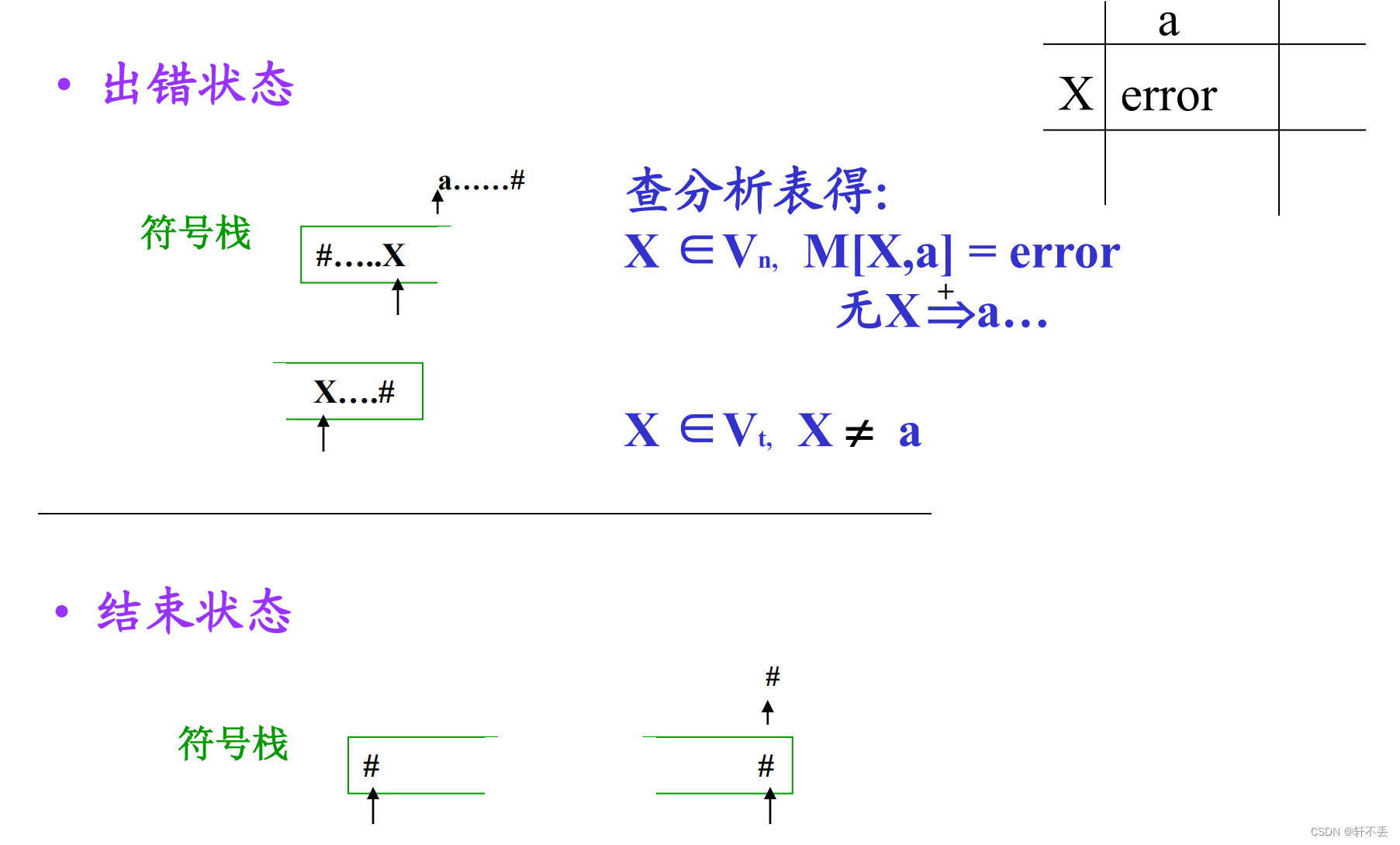
4）執行程序

主要實現如下操作

1. 把#和文法識別符號E推進棧, 讀入下一個符號，重復下述過程直到正常結束或出錯。
2. 測定棧頂符號X和當前輸入符號a,執行如下操作:
   若KaTeX parse error: Expected 'EOF', got '#' at position 5: X=a=#?，分析成功，停止。E匹配輸入串成功。
   若KaTeX parse error: Expected 'EOF', got '#' at position 5: X=a≠#?，把X推出棧，再讀入下一個符號。
   若$X\in V_n$，查分析表M。
   注意a)中U在棧頂！

PS：文法沒有 x→ε，則不需要計算 FOLLOW 集！！！！

五、LL(k)文法

LL(k)是無二義性的文法，其識別的語言都是確定型下推自動機所識別的語言，但反之不能保證一個確定型下推自動機與LL(k)等價。因此關系圖如下：
一個無二義的CFG文法不一定能得到LL(k)文法

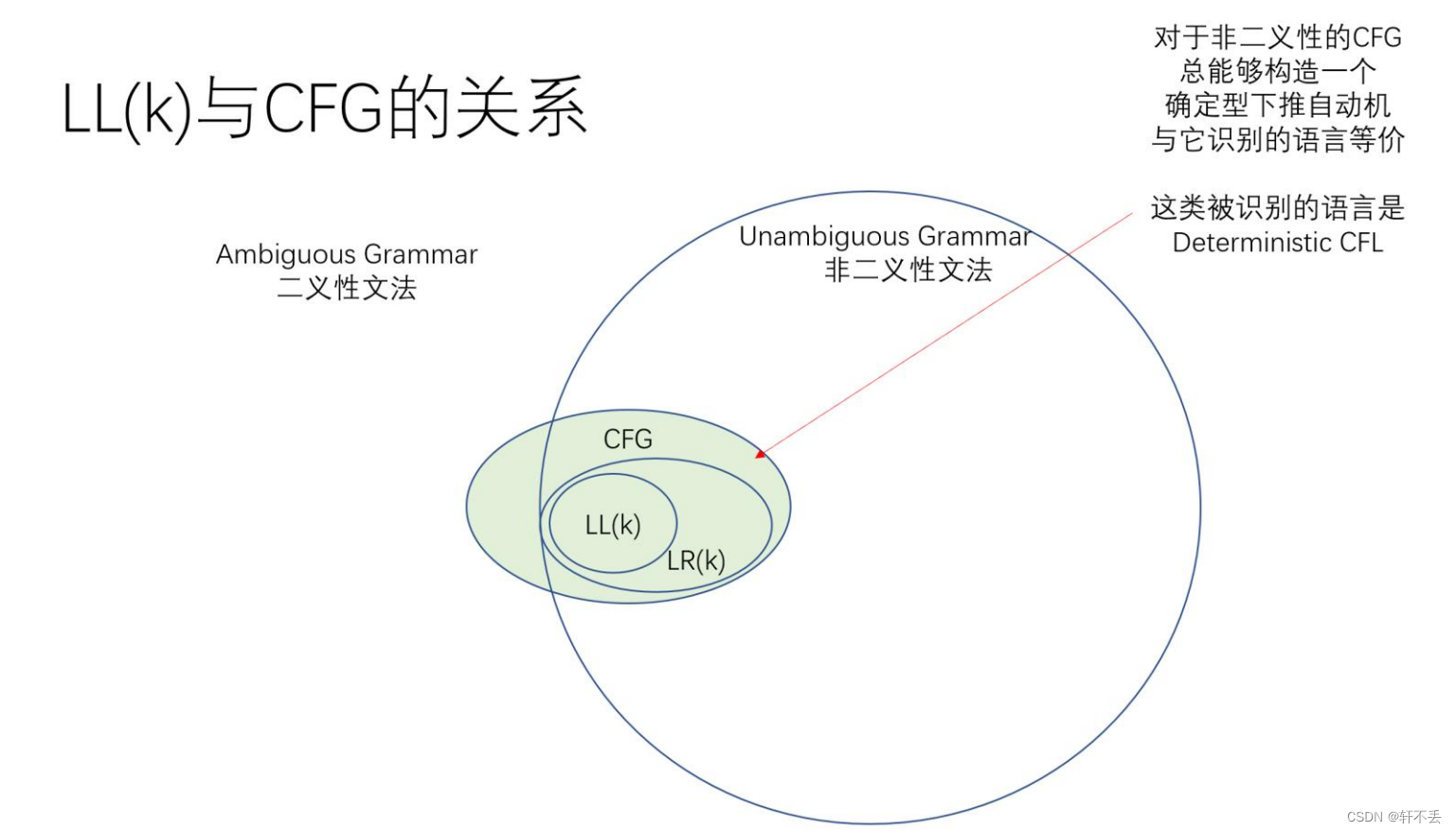
LL(k)文法總是一個LR(k)文法