從線性回歸到神經網絡

一、線性回歸關鍵思想

1、線性模型

2、基礎優化算法

二、線性回歸的從零開始實現

1、生成數據集

2、讀取數據集

3、初始化模型參數

4、定義模型

5、定義損失函數

6、定義優化算法

7、訓練

三、線性回歸的簡潔實現

1、生成數據集

2、讀取數據集

3、定義模型

4、初始化模型參數

5、定義損失函數

6、定義優化算法

7、訓練

一、線性回歸關鍵思想

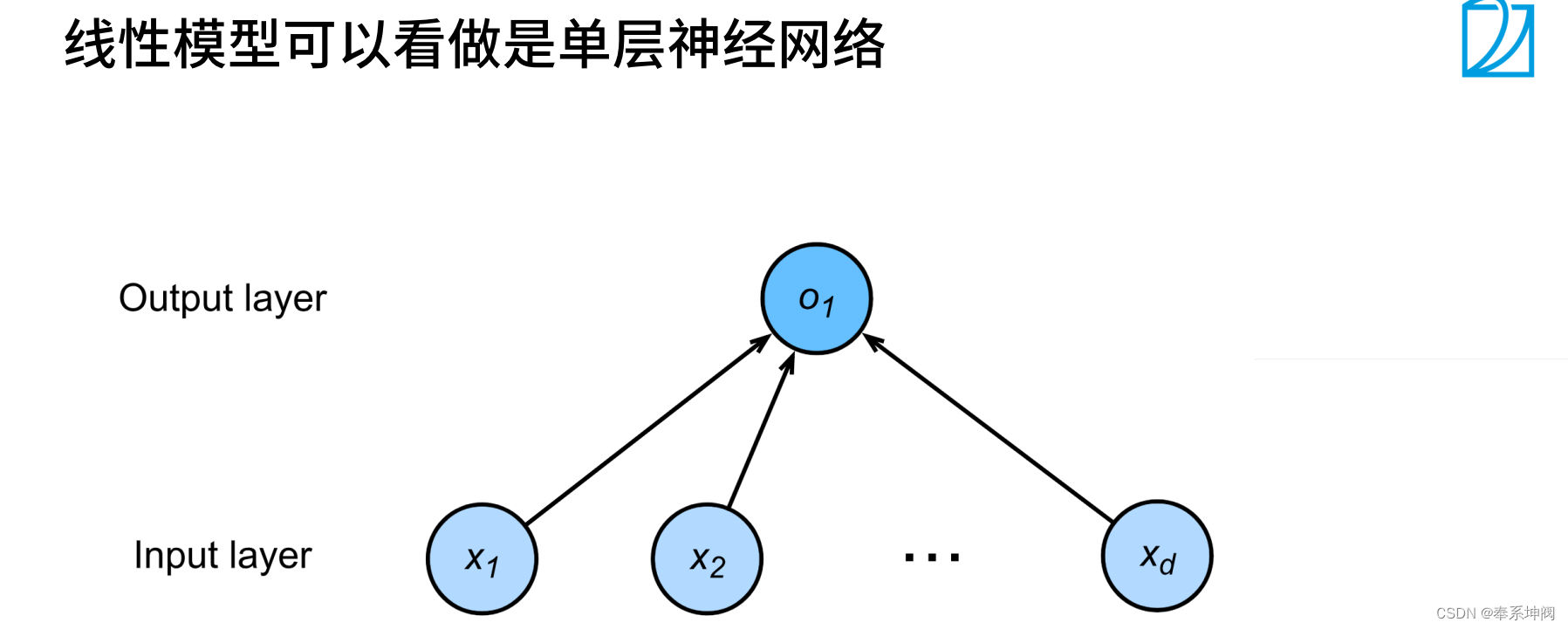
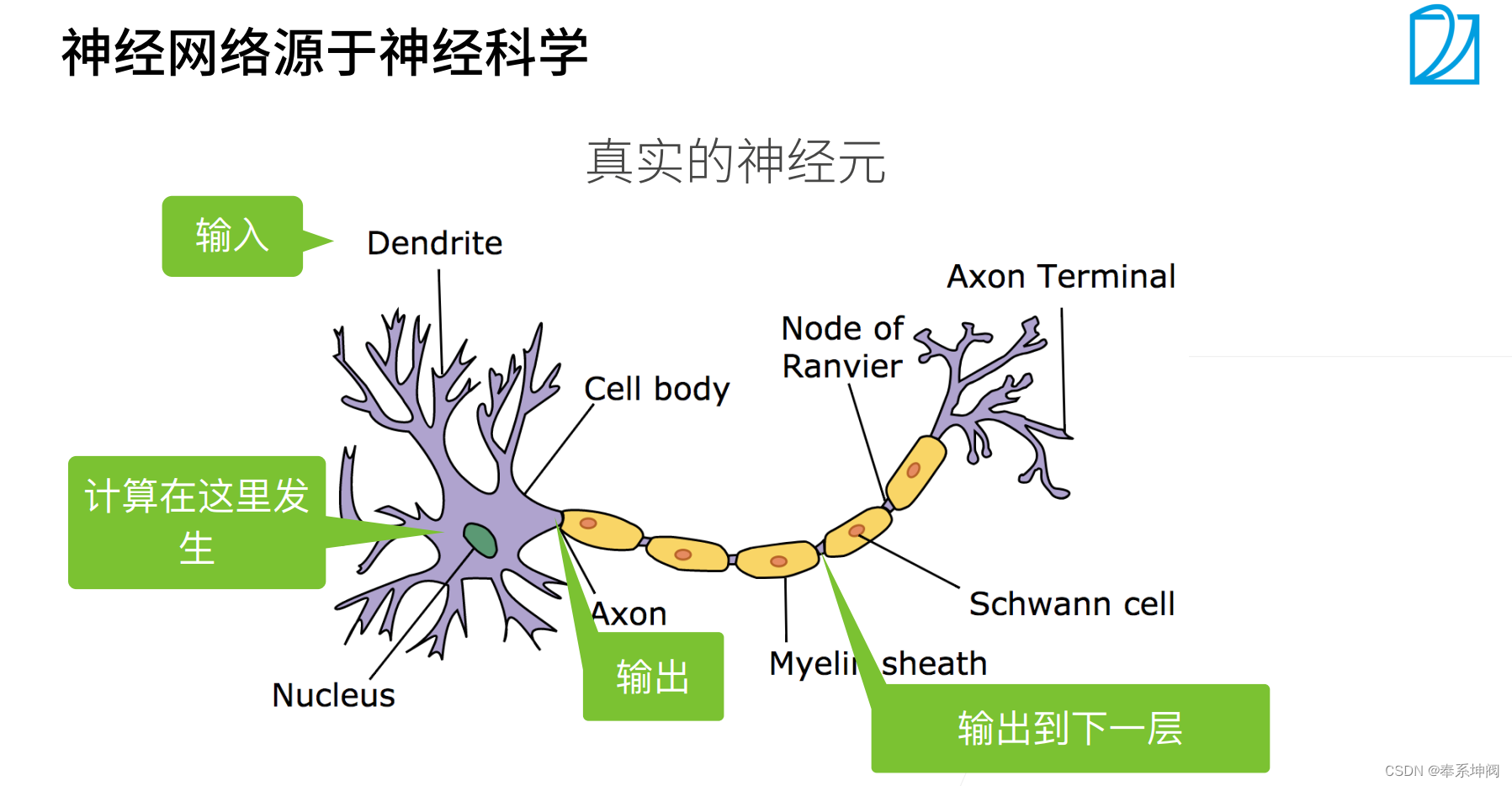
1、線性模型

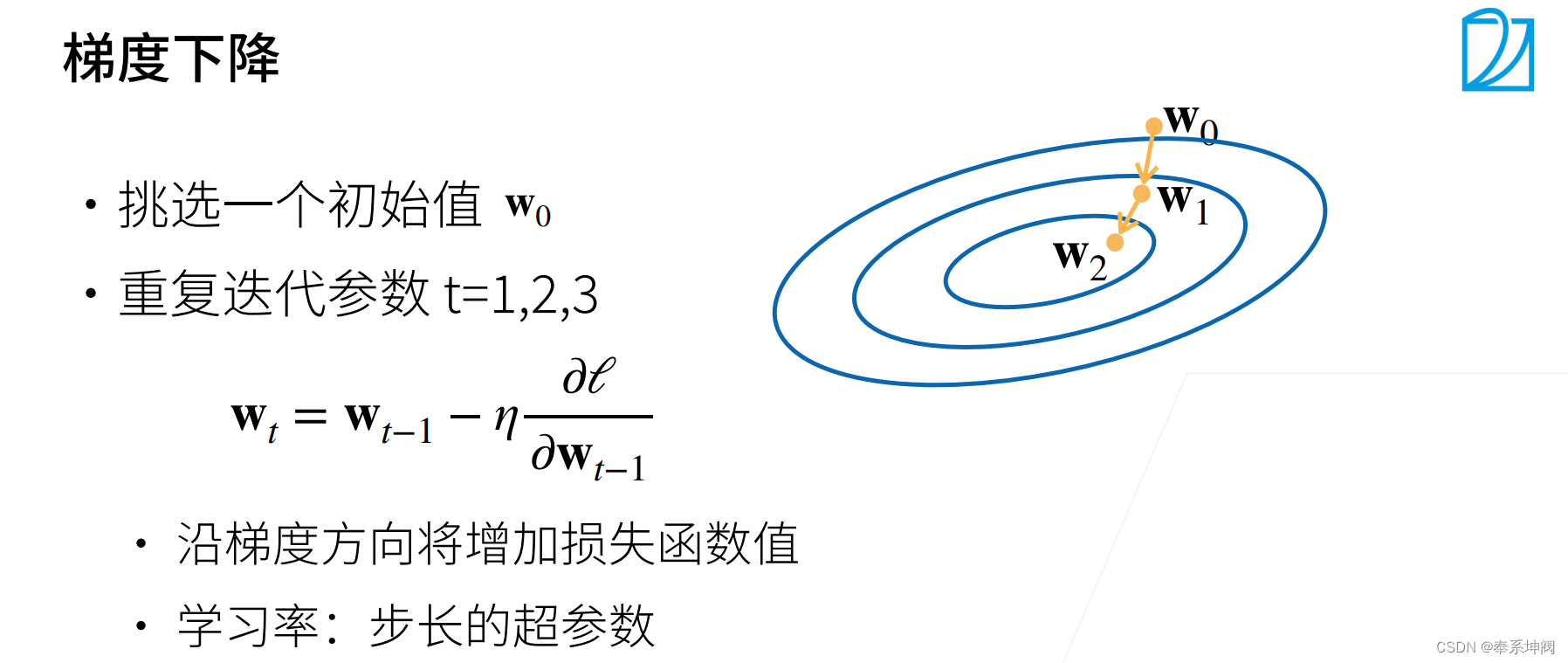
2、基礎優化算法

二、線性回歸的從零開始實現

???????在了解線性回歸的關鍵思想之后，我們可以開始通過代碼來動手實現線性回歸了。在這一節中，我們將從零開始實現整個方法，包括數據流水線、模型、損失函數和小批量隨機梯度下降優化器。雖然現代的深度學習框架幾乎可以自動化地進行所有這些工作，但從零開始實現可以確保我們真正知道自己在做什么。同時，了解更細致的工作原理將方便我們自定義模型、自定義層或自定義損失函數。在這一節中，我們將只使用張量和自動求導。在之后的章節中，我們會充分利用深度學習框架的優勢，介紹更簡潔的實現方式。

import random
import torch
from d2l import torch as d2l

1、生成數據集

???????為了簡單起見，我們將根據帶有噪聲的線性模型構造一個人造數據集。我們的任務是使用這個有限樣本的數據集來恢復這個模型的參數。我們將使用低維數據，這樣可以很容易地將其可視化。

???????在下面的代碼中，我們生成一個包含1000個樣本的數據集，每個樣本包含從標準正態分布中采樣的2個特征。我們的合成數據集是一個矩陣 $\mathbf{X}\in \mathbb{R}^{1000 \times 2}$ （我們使用線性模型參數 $\mathbf{w} = [2, -3.4]^\top$ 、 $b = 4.2$ 和噪聲項 $\epsilon$ 生成數據集及其標簽）：

$\mathbf{y}= \mathbf{X} \mathbf{w} + b + \mathbf\epsilon.$

??????? $\epsilon$ 可以視為模型預測和標簽時的潛在觀測誤差。在這里我們認為標準假設成立，即 $\epsilon$ 服從均值為0的正態分布。為了簡化問題，我們將標準差設為0.01。

???????下面的代碼生成合成數據集。

def synthetic_data(w, b, num_examples):  #@save"""生成y=Xw+b+噪聲w:真實權重 b:真實偏差量 num_examples:生成數據數量"""X = torch.normal(0, 1, (num_examples, len(w)))  # 生成元素均值為0、標準差為1的Xy = torch.matmul(X, w) + by += torch.normal(0, 0.01, y.shape)             # 有偏差量的y值（偏差量均值為0、標準差為0.01）return X, y.reshape((-1, 1))                    # 返回X和有偏差量的y值

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

???????注意，`features`中的每一行都包含一個二維數據樣本，`labels`中的每一行都包含一維標簽值（一個標量）。

print('features:', features[0],'\nlabel:', labels[0])

features: tensor([2.0776e+00, 3.4160e-04]) 
label: tensor([8.3580])

2、讀取數據集

???????訓練模型時要對數據集進行遍歷，每次抽取一小批量樣本，并使用它們來更新我們的模型。由于這個過程是訓練機器學習算法的基礎，所以有必要定義一個函數，該函數能打亂數據集中的樣本并以小批量方式獲取數據。

???????在下面的代碼中，我們定義一個`data_iter`函數，該函數接收批量大小、特征矩陣和標簽向量作為輸入，生成大小為`batch_size`的小批量。每個小批量包含一組特征和標簽。

def data_iter(batch_size, features, labels):num_examples = len(features)indices = list(range(num_examples))# 這些樣本是隨機讀取的，沒有特定的順序random.shuffle(indices)for i in range(0, num_examples, batch_size):batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])      # indices是一個列表，這里是把列表索引在區間[i: min(i + batch_size, num_examples)]的元素列表生成tensoryield features[batch_indices], labels[batch_indices]    # yield用法：https://blog.csdn.net/mieleizhi0522/article/details/82142856

???????通常，我們利用GPU并行運算的優勢，處理合理大小的“小批量”。每個樣本都可以并行地進行模型計算，且每個樣本損失函數的梯度也可以被并行計算。GPU可以在處理幾百個樣本時，所花費的時間不比處理一個樣本時多太多。

???????我們直觀感受一下小批量運算：讀取第一個小批量數據樣本并打印。每個批量的特征維度顯示批量大小和輸入特征數。同樣的，批量的標簽形狀與`batch_size`相等。

batch_size = 10for X, y in data_iter(batch_size, features, labels):    # 注意下面有個break，循環只進行一輪print(X, '\n', y)break

tensor([[ 0.1776, -1.4407],[ 0.5218,  0.1639],[ 1.0650, -0.9711],[-0.1460,  1.1675],[ 0.7669, -1.7807],[ 1.0836, -0.3052],[-0.2531,  0.7157],[-1.6888,  0.1888],[-1.5185,  0.5466],[-0.9307,  1.2468]]) tensor([[ 9.4513],[ 4.6777],[ 9.6400],[-0.0656],[11.7774],[ 7.4136],[ 1.2694],[ 0.2010],[-0.7028],[-1.8955]])

???????當我們運行迭代時，我們會連續地獲得不同的小批量，直至遍歷完整個數據集。上面實現的迭代對教學來說很好，但它的執行效率很低，可能會在實際問題上陷入麻煩。例如，它要求我們將所有數據加載到內存中，并執行大量的隨機內存訪問。在深度學習框架中實現的內置迭代器效率要高得多，它可以處理存儲在文件中的數據和數據流提供的數據。

3、初始化模型參數

???????在我們開始用小批量隨機梯度下降優化我們的模型參數之前，我們需要先有一些參數。在下面的代碼中，我們通過從均值為0、標準差為0.01的正態分布中采樣隨機數來初始化權重，并將偏置初始化為0。

w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

???????在初始化參數之后，我們的任務是更新這些參數，直到這些參數足夠擬合我們的數據。每次更新都需要計算損失函數關于模型參數的梯度。有了這個梯度，我們就可以向減小損失的方向更新每個參數。因為手動計算梯度很枯燥而且容易出錯，所以沒有人會手動計算梯度。我們使用pytorch的自動微分來計算梯度。

4、定義模型

???????接下來，我們必須定義模型，將模型的輸入和參數同模型的輸出關聯起來。回想一下，要計算線性模型的輸出，我們只需計算輸入特征 $\mathbf{X}$ 和模型權重 $\mathbf{w}$ 的矩陣，向量乘法后加上偏置 $b$ 。

???????注意，上面的 $\mathbf{Xw}$ 是一個向量，而 $b$ 是一個標量。回想一下torch中描述的廣播機制：當我們用一個向量加一個標量時，標量會被加到向量的每個分量上。

def linreg(X, w, b):"""線性回歸模型"""return torch.matmul(X, w) + b

5、定義損失函數

???????因為需要計算損失函數的梯度，所以我們應該先定義損失函數。這里我們使用平方損失函數。在實現中，我們需要將真實值`y`的形狀轉換為和預測值`y_hat`的形狀相同。

def squared_loss(y_hat, y):"""均方損失"""return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

6、定義優化算法

???????正如我們在前面討論的，線性回歸有解析解。盡管線性回歸有解析解，但本書中的其他模型卻沒有，因此需要使用優化算法，這里我們介紹小批量隨機梯度下降。

???????在每一步中，使用從數據集中隨機抽取的一個小批量，然后根據參數計算損失的梯度。接下來，朝著減少損失的方向更新我們的參數。下面的函數實現小批量隨機梯度下降更新。該函數接受模型參數集合、學習速率和批量大小作為輸入。每一步更新的大小由學習速率`lr`決定。因為我們計算的損失是一個批量樣本的總和，所以我們用批量大小`batch_size`來規范化步長，這樣步長大小就不會取決于我們對批量大小的選擇。

def sgd(params, lr, batch_size):"""小批量隨機梯度下降"""with torch.no_grad():    # 模型參數更新的時候不需要進行梯度計算for param in params:param -= lr * param.grad / batch_size  # 自動求導，梯度會自動存在于.grad里面，注意這里要除以batch_size，這樣不管batch_size有多大，學習率其實都差不多，這樣學習率更容易調，相當于少個變量param.grad.zero_()    # 用完梯度參數后將梯度設0，防止Pytorch在下次計算時累積梯度

7、訓練

???????現在我們已經準備好了模型訓練所有需要的要素，可以實現主要的訓練過程部分了。理解這段代碼至關重要，因為從事深度學習后，相同的訓練過程幾乎一遍又一遍地出現。

???????在每次迭代中，我們讀取一小批量訓練樣本，并通過我們的模型來獲得一組預測（正向傳播）。計算完損失后，我們開始反向傳播，存儲每個參數的梯度（反向傳播的作用就是根據正向傳播的loss計算梯度）。最后，我們調用優化算法`sgd`來更新模型參數（優化算法的作用就是根據梯度來更新參數值）。

???????概括一下，我們將執行以下循環，重復以下訓練，直到完成：

? ? ? ? ? ? ? ? ? ? ? ?Ⅰ.計算梯度： $\mathbf{g} \leftarrow \partial_{(\mathbf{w},b)} \frac{1}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} l(\mathbf{x}^{(i)}, y^{(i)}, \mathbf{w}, b)$

Ⅱ.更新參數： $(\mathbf{w}, b) \leftarrow (\mathbf{w}, b) - \eta \mathbf{g}$

???????在每個迭代周期（epoch）中，我們使用`data_iter`函數遍歷整個數據集，并將訓練數據集中所有樣本都使用一次（假設樣本數能夠被批量大小整除）。這里的迭代周期個數`num_epochs`和學習率`lr`都是超參數，分別設為3和0.03。設置超參數很棘手，需要通過反復試驗進行調整。我們現在忽略這些細節，以后會詳細介紹。

lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):for X, y in data_iter(batch_size, features, labels):l = loss(net(X, w, b), y)  # X和y的小批量損失# 因為l形狀是(batch_size,1)，而不是一個標量。l中的所有元素被加到一起，# 并以此計算關于[w,b]的梯度l.sum().backward()            # 每一個batch_size計算一次損失，將一個batch的損失求和后反向傳播計算梯度，每次循環算一次梯度就行，后面不再需要計算梯度，sgd里面也是有‘with torch.no_grad()’的sgd([w, b], lr, batch_size)   # 使用參數的梯度更新參數，梯度用完后清零，防止累積with torch.no_grad():    # 關閉梯度運算train_l = loss(net(features, w, b), labels)    # 用當前參數計算所有數據的損失print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

epoch 1, loss 0.039029
epoch 2, loss 0.000140
epoch 3, loss 0.000048

???????因為我們使用的是自己合成的數據集，所以我們知道真正的參數是什么。因此，我們可以通過比較真實參數和通過訓練學到的參數來評估訓練的成功程度。事實上，真實參數和通過訓練學到的參數確實非常接近。

print(f'w的估計誤差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估計誤差: {true_b - b}')

w的估計誤差: tensor([ 4.8280e-05, -2.8586e-04], grad_fn=<SubBackward0>)
b的估計誤差: tensor([0.0010], grad_fn=<RsubBackward1>)

???????注意，我們不應該想當然地認為我們能夠完美地求解參數。在機器學習中，我們通常不太關心恢復真正的參數，而更關心如何高度準確預測參數。幸運的是，即使是在復雜的優化問題上，隨機梯度下降通常也能找到非常好的解。其中一個原因是，在深度網絡中存在許多參數組合能夠實現高度精確的預測。

三、線性回歸的簡潔實現

1、生成數據集

???????與線性回歸的從零開始實現類似，我們首先生成數據集。

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

2、讀取數據集

???????我們可以調用框架中現有的API來讀取數據。我們將`features`和`labels`作為API的參數傳遞，并通過數據迭代器指定`batch_size`。此外，布爾值`is_train`表示是否希望數據迭代器對象在每個迭代周期內打亂數據。

def load_array(data_arrays, batch_size, is_train=True):"""構造一個PyTorch數據迭代器"""dataset = data.TensorDataset(*data_arrays)return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
data_iter = load_array((features, labels), batch_size)

3、定義模型

???????對于標準深度學習模型，我們可以使用框架的預定義好的層。這使我們只需關注使用哪些層來構造模型，而不必關注層的實現細節。我們首先定義一個模型變量`net`，它是一個`Sequential`類的實例。`Sequential`類將多個層串聯在一起。當給定輸入數據時，`Sequential`實例將數據傳入到第一層，然后將第一層的輸出作為第二層的輸入，以此類推。

???????在下面的例子中，我們的模型只包含一個層，因此實際上不需要`Sequential`。但是由于以后幾乎所有的模型都是多層的，在這里使用`Sequential`會讓你熟悉“標準的流水線”。

???????單層網絡架構這一單層被稱為全連接層（fully-connected layer），因為它的每一個輸入都通過矩陣向量乘法得到它的每個輸出。

???????在PyTorch中，全連接層在`Linear`類中定義。值得注意的是，我們將兩個參數傳遞到`nn.Linear`中。第一個指定輸入特征形狀，即2，第二個指定輸出特征形狀，輸出特征形狀為單個標量，因此為1。

# nn是神經網絡的縮寫
from torch import nnnet = nn.Sequential(nn.Linear(2, 1))

4、初始化模型參數

???????在使用`net`之前，我們需要初始化模型參數。如在線性回歸模型中的權重和偏置。深度學習框架通常有預定義的方法來初始化參數。在這里，我們指定每個權重參數應該從均值為0、標準差為0.01的正態分布中隨機采樣，偏置參數將初始化為零。

???????正如我們在構造`nn.Linear`時指定輸入和輸出尺寸一樣，現在我們能直接訪問參數以設定它們的初始值。我們通過`net[0]`選擇網絡中的第一個圖層，然后使用`weight.data`和`bias.data`方法訪問參數。我們還可以使用替換方法`normal_`和`fill_`來重寫參數值。

net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

5、定義損失函數

???????計算均方誤差使用的是`MSELoss`類，也稱為平方 $L_2$ 范數。默認情況下，它返回所有樣本損失的平均值。

loss = nn.MSELoss()

6、定義優化算法

???????小批量隨機梯度下降算法是一種優化神經網絡的標準工具，PyTorch在`optim`模塊中實現了該算法的許多變種。當我們(實例化一個`SGD`實例)時，我們要指定優化的參數（可通過`net.parameters()`從我們的模型中獲得）以及優化算法所需的超參數字典。小批量隨機梯度下降只需要設置`lr`值，這里設置為0.03。

trainer = torch.optim.SGD(net.parameters(), lr=0.03)

7、訓練

???????通過深度學習框架的高級API來實現我們的模型只需要相對較少的代碼。我們不必單獨分配參數、不必定義我們的損失函數，也不必手動實現小批量隨機梯度下降。當我們需要更復雜的模型時，高級API的優勢將大大增加。當我們有了所有的基本組件，訓練過程代碼與我們從零開始實現時所做的非常相似。

???????回顧一下：在每個迭代周期里，我們將完整遍歷一次數據集（`train_data`），不停地從中獲取一個小批量的輸入和相應的標簽。對于每一個小批量，我們會進行以下步驟:

????????????????* 通過調用`net(X)`生成預測并計算損失`l`（前向傳播）。

????????????????* 通過進行反向傳播來計算梯度。

????????????????* 通過調用優化器來更新模型參數。

???????為了更好的衡量訓練效果，我們計算每個迭代周期后的損失，并打印它來監控訓練過程。

num_epochs = 3
for epoch in range(num_epochs):for X, y in data_iter:l = loss(net(X) ,y)    # 正向傳播計算losstrainer.zero_grad()    # 梯度清零，l.backward()會計算這次的梯度，因此要在l.backward()之前進行，不然會將上次的梯度與這次的累加l.backward()           # 反向傳播計算梯度trainer.step()         # 用優化器進行優化l = loss(net(features), labels)print(f'epoch {epoch + 1}, loss {l:f}')

epoch 1, loss 0.000248
epoch 2, loss 0.000103
epoch 3, loss 0.000103

???????下面我們比較生成數據集的真實參數和通過有限數據訓練獲得的模型參數。要訪問參數，我們首先從`net`訪問所需的層，然后讀取該層的權重和偏置。正如在從零開始實現中一樣，我們估計得到的參數與生成數據的真實參數非常接近。

w = net[0].weight.data
print('w的估計誤差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估計誤差：', true_b - b)

w的估計誤差： tensor([-0.0010, -0.0003])
b的估計誤差： tensor([-0.0003])

???????------注：本文圖片和代碼均來自李沐老師的課件，另外加了一些個人注釋，感謝李沐老師分享