🔥博客主頁：?A_SHOWY
🎥系列專欄：力扣刷題總結錄?數據結構??云計算??數字圖像處理? ??
| 28.找出字符串中第一個匹配項的下標 | mid | 經典KMP |
| 4593重復的子字符串 | mid | 可以使用滑動窗口或者KMP |
KMP章節難度較大，需要深入理解其中的底層原理，單純背代碼不可靠
一、KMP方法總結
（1）KMP能解決的問題
KMP主要應用在字符串匹配上
（2）前綴和后綴
前綴：包含首字母不包含尾字母的所有子串
例如：
字符串aabaaf
前綴： aaaaabaabaaabaaaabaaf ×后綴：包含尾字母而不包含首字母的所有子串
字符串aabaaf
后綴： fafaafbaafabaafaabaaf ×（3）最長相等的前后綴?
模式串的前綴表
字符串aabaaf
最長相等前后綴：
a 0
aa 1
aab 0
aaba 1
aabaa 2
aabaaf 0
所以前綴表是010120
所以要跳到最長的相等前后綴的后面去接著匹配
（4）前綴表原理
模式串與前綴表對應位置的數字表示的是：下標i之前的字符串中，有多大長度的相同前后綴，所以當找到不匹配的位置時，要看前一個字符的前綴表的數值，因為要找前一個字符的最長相同的前后綴，前一個字符的前綴表的數值是2， 所以把下標移動到下標2的位置繼續比配。next（prefix）數組：遇到沖突后，要回退到的下一個位置
最重要的一點（理解KMP的核心）：為什么使用前綴表可以告訴我們匹配失敗之后跳到哪里重新匹配？
假設在下標為5的部分不匹配了，下標5之前的這部分字符串最長相等的前后綴是aa，找到了最長的相等前后綴，匹配失敗的地方是后綴子串的后面，那么找到與其相等的前綴部分就可以繼續匹配了。
（5）前綴表代碼實現
1.求next數組方式有很多 （比如原封不動【如果遇到沖突了，就找這個前綴表數組的前一位作為下標】，有的全部右移【初始值為-1，沖突這個位置對應下標】，有的全部減去1【不推薦 】），但是next數組的核心是遇到沖突了要向前回退
2.i指向了后綴末尾，j指向了前綴末尾，還代表i（包括i）之前的子串的最長相等前后綴的長度（這里難點就是j的雙層含義），他非常像一個遞歸的過程
3.具體步驟可以分為四步：初始化 討論處理前后綴不相同的時候 處理前后綴相同的時候 給next數組賦值，就能得到模式串的前綴表
- 首先是初始化，對于 i和j的初始化以及next【0】的初始化，那么j我們初始化為-1，前面提到這只是其中的一種表現形式也就是串整體右移，那么i選擇1（i肯定不能是0），next【i】表示i之前最長前后綴的長度，其實也就是j對于i的初始化我們放在后邊的循環里
int j = -1;
next[0] = j;- 其次就是討論前后綴不相同的情況，比較s【i】和s【j+1】是否相同，如果不同，那么就要回退，由于next【j】記錄著j之前子串相同前后綴的長度，就要找j+1前一個元素在next數組的值（next【j】），注意向前回退是一個持續的過程，所以用while如果不匹配就一直回退
for(int i = 0; i < s.size(); s++){
while(j>=0 && s[i] != s[j+1]){//向前回退j = next[j];
}
}- 然后處理前后綴相同的情況,如果s【i】和s【j+1】相同，，就要同時移動i和j，并且，講j賦值給next【i】
if (s[i] == s[j + 1]) { // 找到相同的前后綴j++;
}
next[i] = j;?所以完整版本的 代碼如下：
void getNext(int* next, const string& s){int j = -1;next[0] = j;for(int i = 1; i < s.size(); i++) { // 注意i從1開始while (j >= 0 && s[i] != s[j + 1]) { // 前后綴不相同了j = next[j]; // 向前回退}if (s[i] == s[j + 1]) { // 找到相同的前后綴j++;}next[i] = j; // 將j（前綴的長度）賦給next[i]}
}二、經典題目
（1）28.找出字符串中第一個匹配項的下標
28. 找出字符串中第一個匹配項的下標
https://leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/其實這個題目可以分成兩個部分，是一個經典的字符串匹配題目，肯定是用我們剛剛學過的KMP算法來完成。那么所謂分成兩個部分解體，第一部分就是構造NEXT數組，第二部分就是運用這個前綴表進行一個匹配的問題，那么第一部分的構造前綴表（NEXT數組）已經寫完了，下面我們來寫匹配過程的代碼。注意我們一直用的是全體-1操作后的NEXT數組，在文本串haystack里面查找是否出現過模式串needle。
int strStr(string haystack, string needle) {int j = -1;int next[needle.size()];getNext(next,needle);for(int i = 0; i< haystack.size();i++)//匹配過程中，next數組的使用從索引0開始{while(j >= 0 && haystack[i] != needle[j+1]){j = next[j];}if(haystack[i] == needle[j+1]){j++;}if(j == needle.size() -1){//j到了末尾return (i-needle.size() +1);//返回首部}}return -1;}這里有幾個要注意的點，第一個是i的初始值，匹配過程中，next數組的使用從索引0開始，在構造next數組的時候，0已經給了初始值了，所以從1開始。
然后就是如何判斷是否包含呢，當i走到了needle的末尾的時候，說明存在匹配，返回首部的數值即可，所以完整的代碼實現為
class Solution {
public:
void getNext(int* next, string& s){int j = -1;next[0] = j;//初始化for(int i =1; i < s.size();i++)//初始化，i從1開始{while(j >= 0 && s[i] != s[j+1]){//如果不想等j = next[j];//j就回退，這里有點像遞歸}if(s[i] == s[j+1]){j++;}next[i] = j;//最后給next數組的i坐標賦值}
}int strStr(string haystack, string needle) {int j = -1;int next[needle.size()];getNext(next,needle);for(int i = 0; i< haystack.size();i++)//匹配過程中，next數組的使用從索引0開始{while(j >= 0 && haystack[i] != needle[j+1]){j = next[j];}if(haystack[i] == needle[j+1]){j++;}if(j == needle.size() -1){//j到了末尾return (i-needle.size() +1);//返回首部}}return -1;}
};（2）459.重復的子字符串
459. 重復的子字符串https://leetcode.cn/problems/repeated-substring-pattern/
方法一：滑動窗口
當一個字符串內部由重復的子串組成，也就是由前后相同的子串組成。那么既然前面有相同的子串，后面有相同的子串，用 s + s，這樣組成的字符串中，后面的子串做前串，前面的子串做后串，就一定還能組成一個s。
所以總體的思路為(個人認為很神奇的思路)：只要兩個s拼接在一起，里面還出現一個s的話，就說明是由重復子串組成。但是注意要去除s+s的字符串的首尾位置，不然判斷沒有意義。
class Solution {
public:bool repeatedSubstringPattern(string s) {string t = s + s;//掐頭去尾t.erase(t.begin());t.erase(t.end() -1);//注意是end-1，應為t.end，返回指向t末尾下一個位置的迭代器if(t.find(s) != std::string::npos)//指的是字符串中未找到指定內容時的特殊返回值return true;return false;}
};方法二：KMP算法
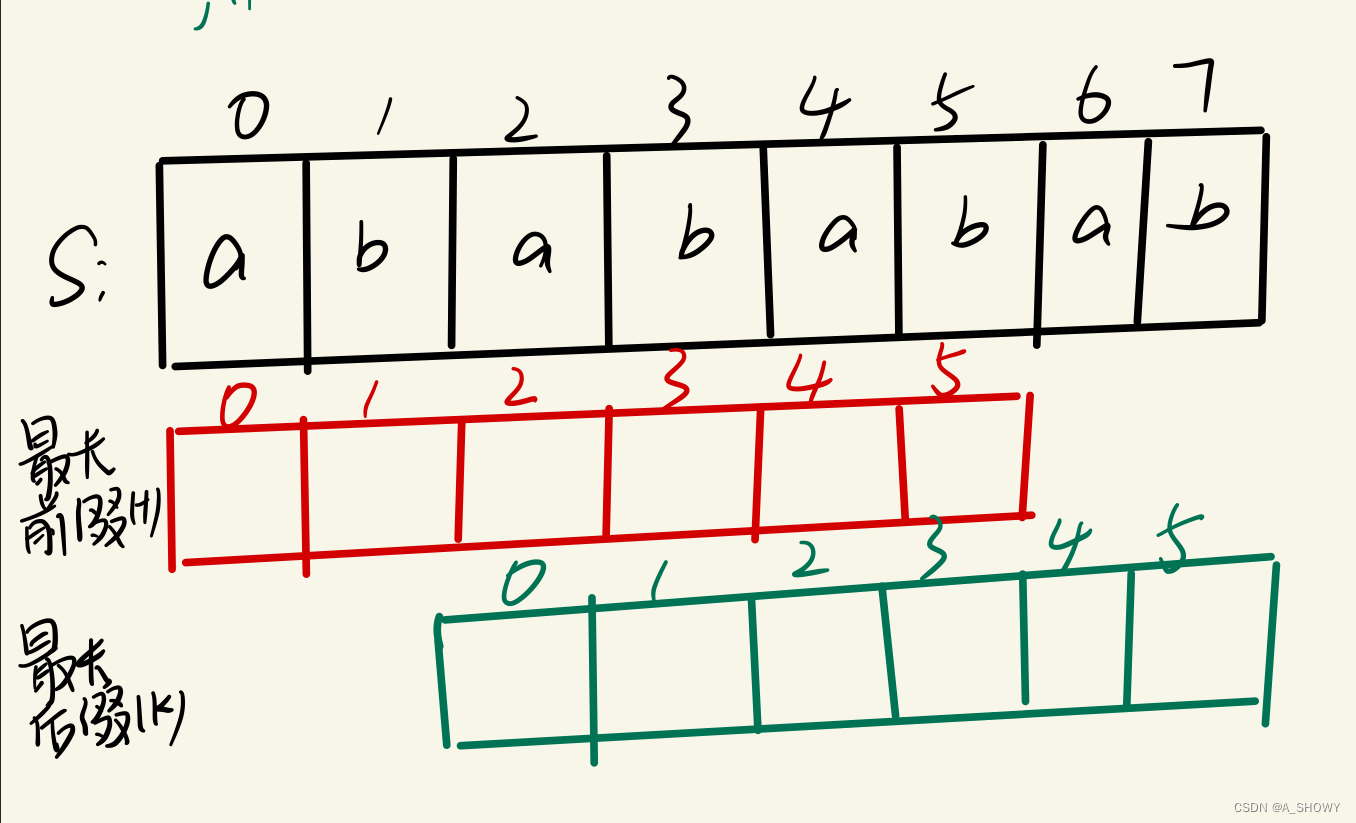
為什么可以使用KMP
步驟一：因為 這是相等的前綴和后綴，t[0] 與 k[0]相同， t[1] 與 k[1]相同，所以 s[0] 一定和 s[2]相同，s[1] 一定和 s[3]相同，即：，s[0]s[1]與s[2]s[3]相同 。
步驟二： 因為在同一個字符串位置，所以 t[2] 與 k[0]相同，t[3] 與 k[1]相同。
步驟三： 因為 這是相等的前綴和后綴，t[2] 與 k[2]相同 ，t[3]與k[3] 相同，所以，s[2]一定和s[4]相同，s[3]一定和s[5]相同，即：s[2]s[3] 與 s[4]s[5]相同。
步驟四：循環往復。
結論：在由重復子串組成的字符串中，最長前后綴不包含的子串就是最小重復子串
最長相等前后綴的長度為：next[len - 1] + 1。(這里的next數組是以統一減一的方式計算的，因此需要+1，如果len % (len - (next[len - 1] + 1)) == 0 ，則說明數組的長度正好可以被 (數組長度-最長相等前后綴的長度) 整除 ，說明該字符串有重復的子字符串。?（仍然是很神奇的思路）
class Solution {
public:void getNext (int* next, const string& s){next[0] = -1;int j = -1;for(int i = 1;i < s.size(); i++){while(j >= 0 && s[i] != s[j + 1]) {j = next[j];}if(s[i] == s[j + 1]) {j++;}next[i] = j;}}bool repeatedSubstringPattern (string s) {if (s.size() == 0) {return false;}int next[s.size()];getNext(next, s);int len = s.size();if (next[len - 1] != -1 && len % (len - (next[len - 1] + 1)) == 0) {return true;}return false;}
};
)
