1. 蒙特霍爾問題

有一個美國電視游戲節目叫做“Let’s Make a Deal”，游戲中參賽者將面對3扇關閉的門，其中一扇門背后有一輛汽車，另外兩扇門后是山羊，參賽者如果能猜中哪一扇門后是汽車，就可以得到它。

通常，當參賽者選定了一扇門時，節目的主持人蒙特霍爾（Monty Hall）會打開剩余兩扇門中的一扇（主持人知道門后是什么），讓你看到門后的山羊，此時會詢問參賽者是否換門，大部分參賽者認為這時關閉的兩扇門中獎的概率是一樣的，即都是1/2，通常他們不會改變他們第一次的選擇。您是否覺得兩個問題幾乎一樣呢？

網上說法很多，我們以標準版：主持人事先知道答案，會打開一扇你沒選擇的門，且其背后一定是羊為條件，其他情況不在此過多的擴展。如下圖所示剩下兩個門供你選擇。

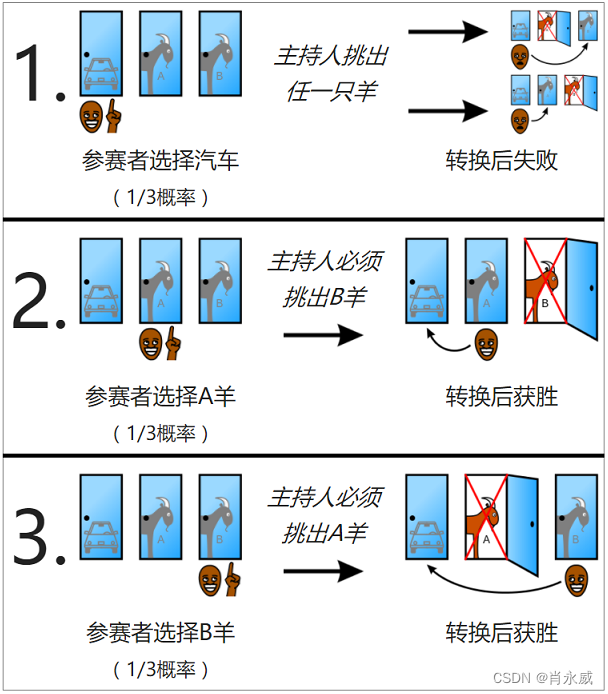
序號	參賽者初選	再選擇換門	結果
1	有車門	有羊門	失敗
2	有羊門A	有車門	獲勝
3	有羊門B	有車門	獲勝

參賽者最初選擇時有1/3的相同概率選擇汽車、羊A和羊B，再選擇轉換后的獲勝概率為2/3。

2. 數學解釋

蒙特霍爾問題的數學證明可以通過貝葉斯定理來完成。我們可以先了解一些定義。

2.1. 貝葉斯定理

2.1.1. 獨立事件概率

我們設定事件$A$的概率為$P(A)$，事件$B$的概率是$P(B)$，且事件$A$和事件$B$是相互獨立的。
則事件$A$和事件$B$同時發生的概率，滿足如下公式：
$P(AB)=P(BA)=P(A)P(B)$

2.1.2. 條件概率

條件概率是在某種條件下，某個事件發生的概率，展示了事件之間的內在聯系和影響。
我們來看兩種條件概率的簡單表述。

1.事件$A$發生之后，事件$B$發生的概率，可以記做$P(B|A)$，此時滿足公式：
$P(B|A)=\frac{P(AB)}{P(A)}$，即 $A$ 和$B$ 同時發生的概率除以 $A$ 發生的概率。
等價于 $P(AB)=P(B|A)P(A)$

2.事件$B$發生之后，事件$A$發生的概率，可以記做$P(A|B)$，此時滿足公式：
$P(A|B)=\frac{P(AB)}{P(B)}$
等價于 $P(AB)=P(A|B)P(B)$

3.綜合這兩種條件事件，可以得到公式：
$P(AB)=P(A|B)P(B)=P(B|A)P(A)$

2.1.3. 貝葉斯公式

我們綜合計算得到一個公式：
$P(A|B)P(B)=P(B|A)P(A)$

這個公式做一個變形可以得到貝葉斯公式：
$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$

2.1.4. 先驗概率和后驗概率

在貝葉斯公式中，還隱含著一些術語：

• $P(A)$是$A$的先驗概率或邊緣概率，它不考慮任何$B$方面的因素。
• $P(A|B)$是$B$發生后$A$的條件概率，由于得自$B$的取值被稱作$A$的后驗概率。

2.2. 貝葉斯定理解釋蒙特霍爾問題

前面我們提到了，關鍵條件在于主持人選擇B門后是無車的，這個事件對于已作出選擇的參賽者來說是否有影響呢？后驗概率是否產生了影響，我們來推導一下：

• 設定A、B、C門后有汽車分別記為事件$A$、$B$、$C$，
  則$P(A)=P(B)=P(C)=\frac{1}{3}$。
• 設定參賽者選擇了A門，由于主持人默認需要選擇沒有汽車的門，因此參賽者的選擇影響了主持人的選擇。
• 設定主持人選擇了B門且沒有汽車，記為事件$D$，
  則$P(D|A)=\frac{1}{2}$（因為如果選手最初選擇了A門，主持人可以選擇打開B或C，而汽車在B或C的概率相等）
  $P(D|B)=0$（因為主持人不會打開選擇的門）
  $P(D|C)=1$（因為如果選手最初選擇了C門，主持人只能選擇打開B門）。
• 在主持人選擇B門無汽車后，參賽者選擇A門有車的概率為$P(A|D)$，即事件$D$發生后事件$A$的概率，由貝葉斯公式得：
  $P(A|D)=\frac{P(D|A)P(A)}{P(D)}$
• 通過前面的分析，我們只需要求$P(D|A)$、$P(A)$、$P(D)$三個元素即可。
  • $P(D|A)$表示A門有汽車的情況下，主持人選擇B門的概率，其為$\frac{1}{2}$;
  • $P(A)$表示A門有汽車的概率，其為$\frac{1}{3}$;
  • $P(D)$可以從全概率公式求得，其為$\frac{1}{2}$：
    $P(D)=P(D|A)P(A)+P(D|B)P(B)+P(D|C)P(C)$
    $P(D)=\frac{1}{2}\times \frac{1}{3}+0\times \frac{1}{3}+1\times \frac{1}{3}=\frac{1}{2}$
• 綜上得到：
  $P(A|D)=\frac{P(D|A)P(A)}{P(D)}=\frac{\frac{1}{2}\times \frac{1}{3}}{2}=\frac{1}{3}$

在主持人選擇B門開啟后無汽車的情況下，參賽者選A門有汽車的概率$P(A|D)=\frac{1}{3}$，因此后驗概率并沒有發生變化，并不是直觀的$\frac{1}{2}$，而仍然是$\frac{1}{3}$。

因此，如果做調換門，那么相當于參賽者選擇了C門，計算過程類似，概率為$\frac{2}{3}$：
$P(C|D)=\frac{P(D|C)P(C)}{P(D)}$
$P(C|D)=\frac{1\times \frac{1}{3}}{\frac{1}{2}}=\frac{2}{3}$

3. 歧義的理解，擴展條件

3.1. 概述

蒙特霍爾問題之所以那么多年來爭論不休，本質上是由于語義理解上的歧義；事實上，根據不同的理解方式，蒙特霍爾問題一共有 4 個本質不同的版本。如果不了解其他版本的話，那當你在現實中遇到其他蒙特霍爾問題的變體時，也會很容易想當然地給出錯誤的答案。

其實，這個問題一共有兩個“歧義”點，缺一不可：

• 主持人是否能確保避免打開正確答案？
• 主持人是否一定會驗證一個和你選擇不同的門？

3.2. 歧義4個版本

根據這兩個問題的答案，我們就得到了這個問題的 4 個版本：

• 版本1（標準版）：主持人事先知道答案，會打開一扇你沒選擇的門，且其背后一定是羊；（1-是；2-是）
• 版本2（驗證版）：主持人事先并不知道答案，隨機打開了一扇你沒選擇的門，其背后恰好是羊；（1-否；2-是）
• 版本3（機選版）：主持人讓系統隨機打開一扇背后是羊的門，它恰好打開了一扇你沒選擇的門；（1-是；2-否）
• 版本4（隨機版）：主持人讓系統隨機打開一扇門，它恰好打開了一扇你沒選擇的門，且其背后是羊；（1-否；2-否）

注：1與2是指上面的歧義點。

那么，我們該怎么理解這 4 個版本的不同之處呢？它們的本質不同在于：主持人的行為是否需要承擔泄露結果的「風險」，使得「條件概率」發生變動。易見，在最初的狀態下，我們選中汽車的概率是 1/3。

• 版本1（標準版） ，無論我們是否選中汽車，主持人總能找到 1 個背后是羊的門，這件事情是 100% 能達成的，所以概率分布完全沒變，我們選中汽車的概率依然為 1/3；
• 版本2（驗證版），主持人顯然冒了風險，如果你選中了羊，那他有 1/2 的概率會選中汽車，所以我們選中汽車的條件概率變成了 （1/3） /（ 1/3+2/3×1/2）=1/2；
• 版本3（機選版），主持人其實也冒了風險，雖然不可能打開背后是汽車的門，但是在你選中羊的時候，有 1/2 的概率會隨機你選擇的門，所以我們選中汽車的條件概率變成了 （1/3） /（1/3+2/3×1/2）=1/2；
• 版本4（隨機版），主持人顯然冒了雙重風險，一個風險是，打開了你選擇的門；另一個風險是，它打開了你沒選擇的門，但其背后是汽車；在這種情況下，條件概率的分子分母都會變化；我們選中汽車的條件概率變成了（1/3×2/3）/（1/3×2/3+2/3×1/3）=1/2

除了「標準版」的答案是 1/3（應該換門）外，其他版本的答案均為 1/2 （換不換均可）。

由此可見，同一件事物對于不同人甚至掌握不同信息的同一個人概率可能不同。因此，概率并不能寄托在實際的物體上，而是存在于條件之下。

參考：

曾加. 蒙提霍爾問題（又稱三門問題、山羊汽車問題）的正解是什么？. 知乎. 2022.04