1、符合規定的三角剖分

1.1、定義

????????如果三角形的任何面的外接圓在其內部不包含頂點，則該三角形是 Delaunay 三角形。 約束 Delaunay 三角形是一種盡可能接近 Delaunay 的約束三角形。 約束 Delaunay 三角形的任何面的外接圓在其內部不包含從該面可見的數據點。

????????如果一條邊內接于一個空圓（其內部不包含數據點），則該邊被稱為德勞內邊。如果這條邊的直徑圓是空的，則該邊被稱為加布里埃爾邊。

????????如果每個約束邊都是一個Delaunay邊，則稱約束Delaunay三角剖分是保形的Delaunay三角剖分。由于約束Delaunay三角剖分中的任何邊要么是Delaunay邊，要么是約束邊，因此保形的Delaunay三角剖分實際上是一個Delaunay三角剖分。唯一的區別是其中一些邊被標記為約束邊。

????????如果每個約束邊都是加布里埃爾邊，則受約束的德勞內三角網被稱為一致的加布里埃爾三角網。 加布里埃爾屬性比德勞內屬性更強，每個加布里埃爾邊都是德勞內邊。 因此，一致的加布里埃爾三角網也是一致的德勞內三角網。

????????任何受約束的Delaunay三角剖分都可以通過在受約束的邊上添加稱為Steiner頂點的頂點，將其細化為一致的Delaunay三角剖分或一致的Gabriel三角剖分，直到它們被分解為足夠小的子約束，成為Delaunay或Gabriel邊。

1.2、構建符合規定的三角剖分

????????約束Delaunay三角剖分可以通過以下兩個全局函數細化為符合規定的三角剖分：

template<class CDT>
void make_conforming_Delaunay_2 (CDT& t)
template<class CDT>
void make_conforming_Gabriel_2 (CDT& t)

????????在這兩種情況下，模板參數CDT必須由受約束的Delaunay三角剖分類實例化（參見第2章“三角剖分”）。

????????用于實例化參數CDT的約束Delaunay三角剖分的幾何特征必須是概念ConformingDelaunayTriangulationTraits_2的模型。

????????受約束的Delaunay三角剖分t通過引用傳遞，并通過添加頂點細化為符合規定的Delaunay三角剖分或符合規定的Gabriel三角剖分。建議用戶在原始三角剖分必須保留用于其他計算的情況下，對輸入三角剖分進行復制。

????????make_conforming_Delaunay_2() 和 make_conforming_Gabriel_2() 使用的算法構建了內部數據結構，如果連續調用這兩個函數，則需要對這些數據結構進行兩次計算。為了避免這些數據被構造兩次，高級用戶可以使用 Triangulation_conformer_2<CDT>?類將約束 Delaunay 三角網細分為符合 Delaunay 三角網，然后再細分為符合 Gabriel 三角網。為了對細化算法進行額外控制，該類還提供了單獨的函數，一次插入一個 Steiner 點。?

1.3、范例

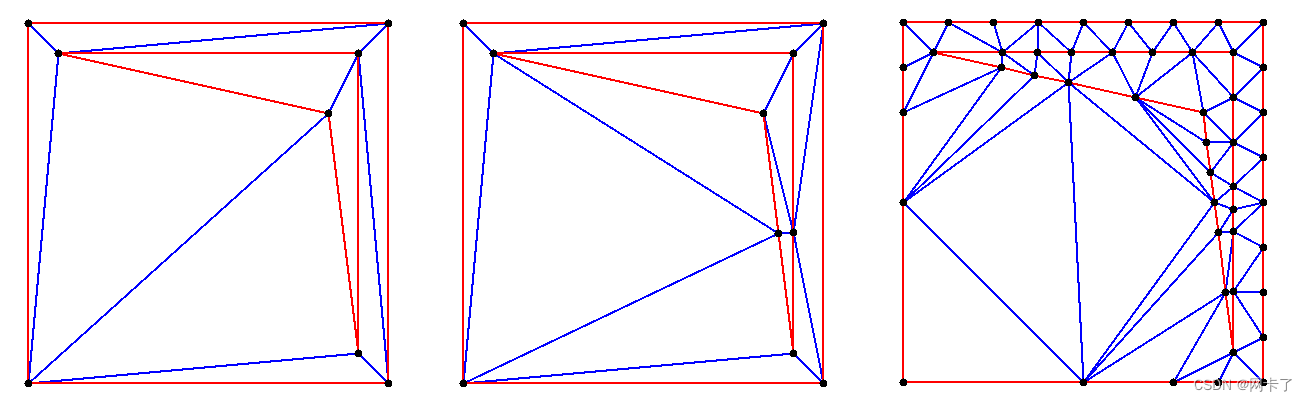
?????????從左到右：初始Delaunay三角剖分、相應的一致Delaunay和相應的Gabriel三角剖分。

2、網格

2.1、定義

????????網格是將給定區域劃分為形狀和大小滿足若干標準的單形。

????????域是用戶想要網格化的區域。它必須是平面的有界區域。域由平面直線圖定義，簡稱為Pslg，它是一組線段，其中兩條線段要么不相交，要么共享一個端點。Pslg的線段是約束，將由網格中的邊集表示。Pslg還可以包含孤立點，這些孤立點將作為網格的頂點出現。

????????Pslg的段可以是邊界段或內部約束段。Pslg的段必須覆蓋域的邊界。

????????Pslg將平面劃分為幾個連通分量。默認情況下，域是有界連通分量的并集。

????????下圖顯示了不使用種子點定義的域的示例及其可能的網格。

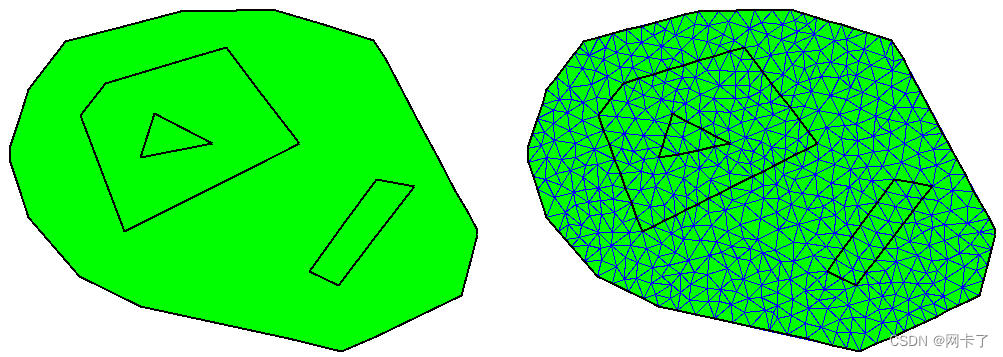
????????定義的域沒有種子點和生成的網格。

????????用戶可以通過提供一組種子點來覆蓋此默認值。種子點標記要網格化的組件，或者標記不要網格化（孔）的組件。?

????????關于用相同的Pslg和用于定義孔的兩個種子點定義的另一個域，請參見下圖。在相應的網格中，這兩個孔是三角形的，但不是網格。

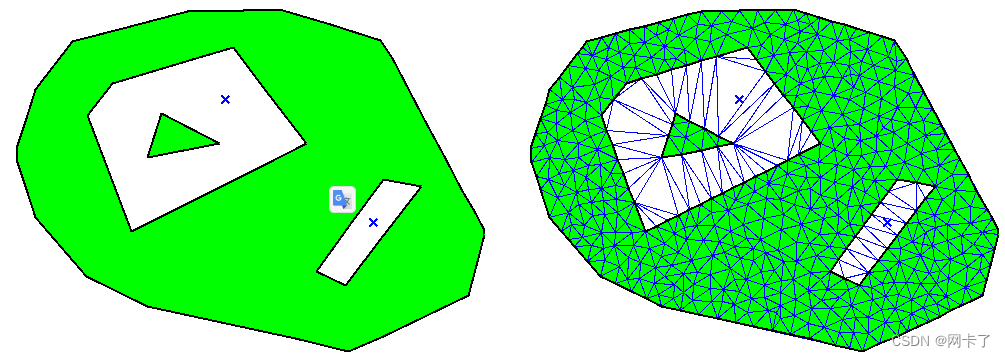
????????具有兩個種子點的域，定義孔和生成的網格。?

2.2、形狀和尺寸標準

????????三角形形狀標準是圓半徑與最短邊長之比的下界B。這樣的界意味著三角形最小角度的下界為arcsin(1/2)B，最大角度的上界為π-2*arcsin(1/2)B。不幸的是，只有當B≥2√時，算法的終止才有保證，這對應于角度的下界為20.7度。

????????大小標準可以是任何傾向于偏好小三角形的標準。例如，大小標準可以是三角形最長邊的長度的上限，或者外接圓半徑的上限。大小限制可以在域中變化。例如，對于與給定線相交的三角形，大小標準可以規定一個較小的尺寸。

????????這兩種類型標準都定義在對象criteria中，并作為參數傳遞給網格化函數。

2.3、網格剖分算法

????????網格問題的輸入是一個Pslg和一組描述要網格化的域的種子，以及一組尺寸和形狀標準。此包中實現的算法從輸入Pslg的約束Delaunay三角劃分開始，并使用Delaunay細化方法生成網格。此方法將新頂點插入三角劃分中，盡可能遠離其他頂點，并在滿足標準時停止。

????????如果輸入Pslg的入射段之間的所有角度都大于60度，并且如果圓周率/邊比的界限大于2√，則該算法保證終止于滿足尺寸和形狀標準的網格。

????????如果某些輸入角度小于 60 度，算法最終將得到一個網格，其中一些三角形在小輸入角度附近違反了標準。這是不可避免的，因為輸入段形成的小角度無法被抑制。此外，已經證明，某些具有小輸入角度的域不能以甚至小于小輸入角度的角度進行網格劃分。請注意，如果域是多邊形區域，則生成的網格將滿足除小輸入角度之外的大小和形狀標準。此外，該算法可能成功地產生角度下限大于 20.7 度的網格，但沒有任何保證。

2.4、構建網格

template<class CDT, class NamedParameters>
void refine_Delaunay_mesh_2 (CDT &t, NamedParameters np)

????????模板參數CDT必須由受約束的Delaunay三角剖分類實例化。

????????CDT 的幾何特征類必須是概念 DelaunayMeshTraits_2 的模型。這個概念通過添加幾何謂詞和構造函數來細化概念 ConformingDelaunayTriangulationTraits_2。

????????第二個模板參數 NamedParameters 允許傳遞一系列種子點來定義域。它還允許傳遞三角形必須滿足的網格化標準。該標準必須是 MeshingCriteria_2 的模型。?

????????CGAL為這個概念提供了兩個模型：

????????Delaunay_mesh_criteria_2<CDT>，定義了一個形狀標準，限制三角形的最小角度，
Delaunay_mesh_size_criteria_2<CDT>，它為前面的標準添加了一個最大邊長度的限制。

????????如果使用不同的標準對同一個三角網格調用函數 refine_Delaunay_mesh_2() 多次，則算法會在每次調用時重建用于網格化的內部數據結構。為了避免每次調用時重建數據結構，高級用戶可以使用類 Delaunay_mesher_2<CDT>。這個類還提供了逐步函數。這些函數一次插入一個頂點。

????????Delaunay_mesher_2<CDT>?類型的任何對象都是從對 CDT 的引用構造的，并且具有幾個成員函數來定義要網格化的域并對 CDT 進行網格化。有關詳細信息，請參見下面給出的示例和參考手冊。請注意，在 Delaunay_mesher_2<CDT>?對象的生存期內，不應從外部修改 CDT。

????????一旦構建了網格，就可以使用面類型的 is_in_domain() 成員函數來確定三角剖分中的哪些面位于網格域中。?

2.5、Lloyd法優化網格

????????該包還提供了一個全局函數，用于在Delaunay精化生成的網格上運行Lloyd優化迭代。這種網格優化的目標是改善網格內部的角度，并使其盡可能接近60度。

template< class CDT >
Mesh_optimization_return_code lloyd_optimize_mesh_2(CDT& cdt);

?????????請注意，此全局函數有幾個命名參數來調整優化過程。

????????該優化過程交替地將頂點重新定位到其Voronoi單元的質心，并更新三角剖分的Delaunay連通性。質心是根據一個尺寸函數計算的，該函數旨在保持Delaunay細化生成的網格中點的局部密度。

????????下圖，這是由refine_Delaunay_mesh_2()生成并使用lloyd_optimize_mesh_2()優化的網格。下圖顯示了這些網格內角度的直方圖。

????????（左）由refine_Delanay_mesh2（）生成的網格，用于統一大小調整標準。（右）顯示了Lloyd優化100次迭代后的相同網格。?

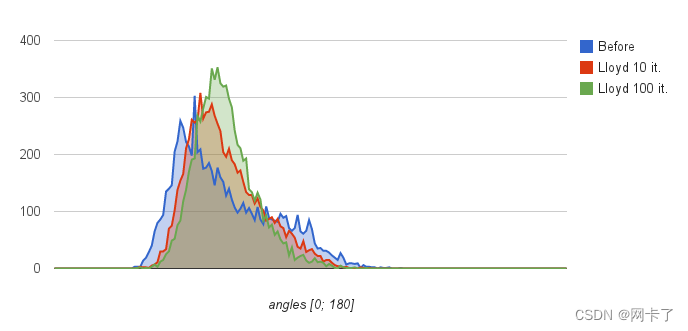
?????????Delaunay細化后以及Lloyd優化的10次和100次迭代后網格內部角度的直方圖。Delaunay精化后，角度在[28.5；121.9]度的區間內。經過10次Lloyd優化迭代后，它們處于[29.1；110.8]。100次迭代使它們達到[29.3；109.9]。

3、輸入\輸出

????????可以使用函數 ATTRIBUTE::IO::write_VTU()導出VTU中的網格結果。有關此格式的更多信息，請參閱VTK（VTU / VTP）文件格式。