1.插入排序
思路:插入排序將一個數插入一個有序的數組里面,將這個數和數組元素挨著比較,直到他插入到合適的位置。
動畫演示:

步驟:1.定義一個變量tmp保存要插入的數據
2.在循環中用tmp和有序數組中的元素比較(比方說要和a[end]比較,如果tmp<a[end]的話,就將a[end]右移動到a[end+1],如果tmp>a[end]的話就直接結束循環,因為已經找到了自己的位置,就是a[end+1].
3.當循環結束則表明已經找到了tmp的位置,下標為end+1,將tmp賦值給a[end+1]即可。
代碼實現
void InsertSort(int* a, int n)
{for (int i = 0; i < n-1; i++){int end = i;int tmp = a[end + 1];while (end >=0){if (tmp < a[end]){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}}
直接插入排序的特性總結:
- 元素集合越接近有序,直接插入排序算法的時間效率越高
- 時間復雜度:O(N^2)
- 空間復雜度:O(1),它是一種穩定的排序算法
- 穩定性:穩定
2.希爾排序
希爾排序( 縮小增量排序 )
希爾排序法又稱縮小增量法。希爾排序法的基本思想是:先選定一個整數,把待排序文件中所有記錄分成個組,所有距離為的記錄分在同一組內,并對每一組內的記錄進行排序。然后,取,重復上述分組和排序的工作。當到達=1時,所有記錄在統一組內排好序。相當于分組的插入排序。
步驟:
1.將要排列的數據分為幾組
2.每一組內進行插入排序。
3.縮小組數,當組數為1時,相當于直接插入排序。
void ShellSort(int* a, int n)
{int gap = 3;for (int i = 0; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
上面代碼為單組的排序,只有一組。
void ShellSort(int* a, int n)
{int gap = 3;for (int j = 0; j < gap; j++){for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}}
加了循環,將每組都排好序,但是整體沒有有序。當gap!=1時,屬于預排序。每次循環減小gap的值。說明分組在變,然后在每一組里面繼續排序,當gap等于1時,相當于插入排序。
void ShellSort(int* a, int n)
{int gap = 3;while (gap >= 1){gap /= 2;for (int j = 0; j < gap; j++){for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}}}
上面這種是一組排,會多套一層循環。如果使用下面的代碼是一組沒排完,就進行排下一組,一組中先把前兩個元素排好,在排第二組的前兩個元素,當排完每一組的前兩個元素,又回到第一組,排第一組的前三個元素,排好前三個元素,接著排第二組的前三個元素,依次類推。
時間復雜度平均:O(N^1.3)
空間復雜度:O(1)
3.選擇排序
基本思想:
每一次從待排序的數據元素中選出最小(或最大)的一個元素,存放在序列的起始位置,直到全部待排序的
數據元素排完 。
步驟:1.定義兩個變量maxi,mini分別記錄要排序數據的最大值和最小值的下標。初始將·maxi,mini等于起始下標。
2.循環遍歷要排序的數據,更新下標,如果有數據大于a[maxi],maxi更新為當前的i;如果有數據小于a[mini],mini更新為當前的i;
3.交換此時最小值和第一個數據的位置,最大值和最后一個數據的位置,已經保證了兩個數據到他該有的位置。起始位置下標++,結束位置下標–;
4.然后就要排除已經排好的兩個元素,現在maxi與mini起始下標就為第二個元素下標了。
5.循環條件起始位置下標小于結束位置下標。
動畫演示:

代碼實現:
void SelectSort(int* a, int n)
{int begin = 0;int end = n - 1;while (begin < end){int maxi = begin;int mini = begin;for (int i = begin + 1; i <=end; i++){if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}swap(&a[begin], &a[mini]);swap(&a[end], &a[maxi]);begin++;end--;}}
如果你要排序的數據里面最大的數據不是第一個的話,上面的代碼你會覺得是正確的,如果第一個數據是最大的,排序就不對了,到底是為什么呢?我們可以調試調試

修改代碼為:
void SelectSort(int* a, int n)
{int begin = 0;int end = n - 1;while (begin < end){int maxi = begin;int mini = begin;for (int i = begin + 1; i <=end; i++){if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}swap(&a[begin], &a[mini]);if (maxi == begin){maxi = mini;}swap(&a[end], &a[maxi]);begin++;end--;}}
直接選擇排序的特性總結:
時間復雜度:O(N^2)
空間復雜度:O(1)
4.堆排序
堆排序是指利用堆積樹(堆)這種數據結構所設計的一種排序算法,它是選擇排序的一種。它是通過堆來進行選擇數據。需要注意的是排升序要建大堆,排降序建小堆。
void AdjustDwon(int* a, int n, int root)//向下調整建立大堆。
{int child = root * 2 + 1;while (child < n){if (child+1<n &&a[child] < a[child + 1]){child = child + 1;}if (a[child] > a[root]){swap(&a[child], &a[root]);root = child;child = root * 2 + 1;}else{break;}}}
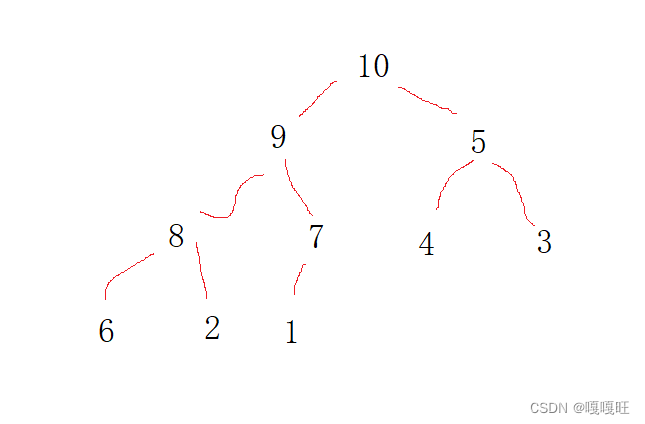
上圖為建立的大堆。
堆排序演示
5.冒泡排序
思路:
左邊大于右邊交換一趟排下來最大的在右邊
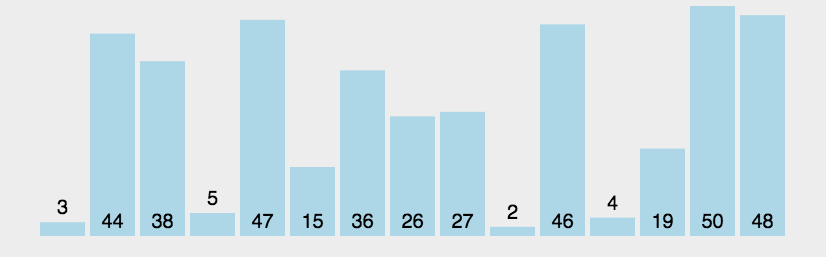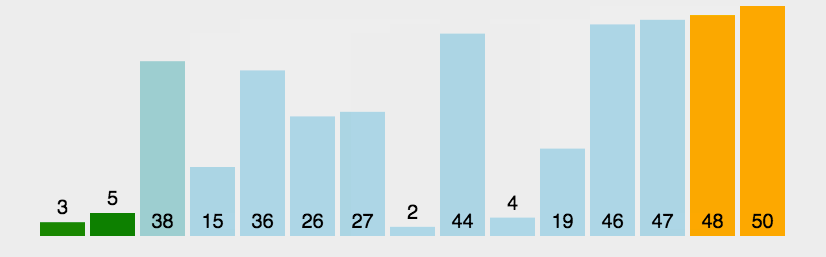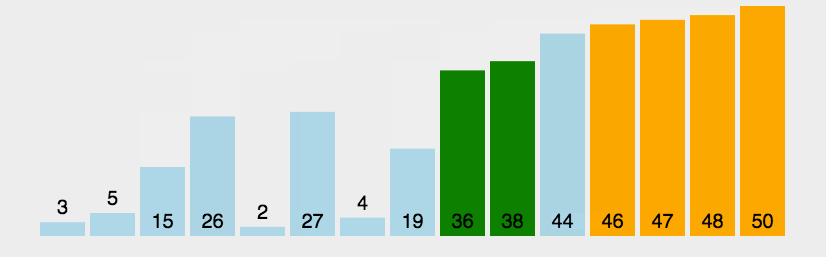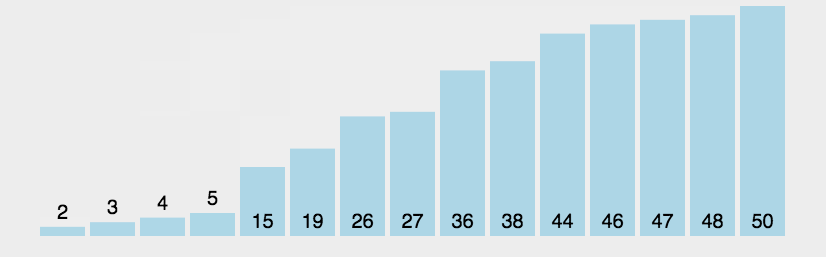
代碼實現:
void BubbleSort(int* a, int n)
{for (int i = 0; i < n-1; i++){for (int j = 0; j < n - i-1; j++){if (a[j + 1] < a[j]){swap(&a[j], &a[j + 1]);}}}}
時間復雜度:O(N^2)
空間復雜度:O(1)
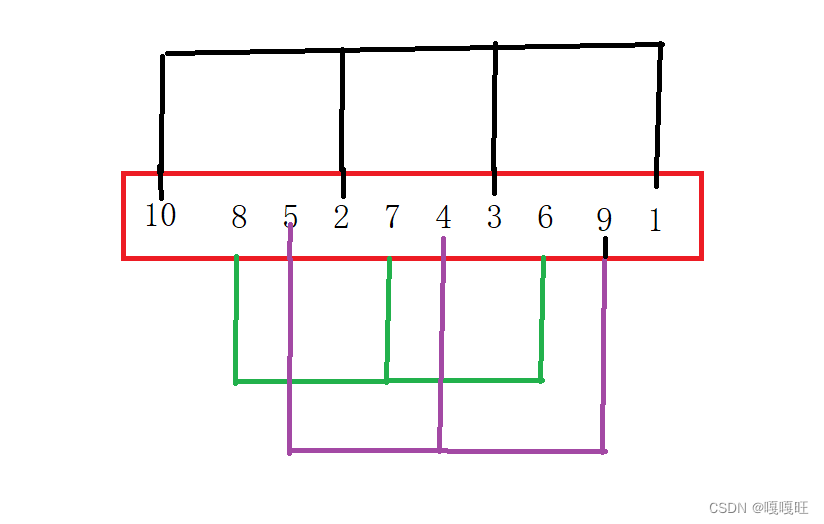




![隊列排序:給定序列a,每次操作將a[1]移動到 從右往左第一個嚴格小于a[1]的元素的下一個位置,求能否使序列有序,若可以,求最少操作次數](http://pic.xiahunao.cn/隊列排序:給定序列a,每次操作將a[1]移動到 從右往左第一個嚴格小于a[1]的元素的下一個位置,求能否使序列有序,若可以,求最少操作次數)



)








真題解析)

