版本說明
當前版本號[20231205]。
| 版本 | 修改說明 |
|---|---|
| 20231205 | 初版 |
目錄
文章目錄
- 版本說明
- 目錄
- 到達首都的最少油耗
- 理解題目
- 代碼思路
- 參考代碼
原題可以點擊此 2477. 到達首都的最少油耗 前去練習。
到達首都的最少油耗
? 給你一棵 n 個節點的樹(一個無向、連通、無環圖),每個節點表示一個城市,編號從 0 到 n - 1 ,且恰好有 n - 1 條路。0 是首都。給你一個二維整數數組 roads ,其中 roads[i] = [ai, bi] ,表示城市 ai 和 bi 之間有一條 雙向路 。
? 每個城市里有一個代表,他們都要去首都參加一個會議。
? 每座城市里有一輛車。給你一個整數 seats 表示每輛車里面座位的數目。
? 城市里的代表可以選擇乘坐所在城市的車,或者乘坐其他城市的車。相鄰城市之間一輛車的油耗是一升汽油。
? 請你返回到達首都最少需要多少升汽油。
示例 1:
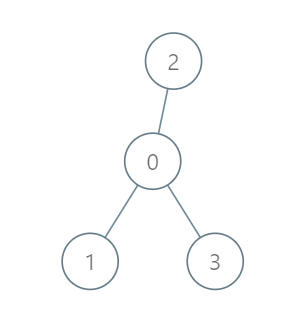
輸入:roads = [[0,1],[0,2],[0,3]], seats = 5
輸出:3
解釋:
- 代表 1 直接到達首都,消耗 1 升汽油。
- 代表 2 直接到達首都,消耗 1 升汽油。
- 代表 3 直接到達首都,消耗 1 升汽油。
最少消耗 3 升汽油。
示例 2:
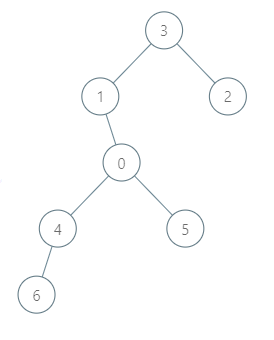
輸入:roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2
輸出:7
解釋:
- 代表 2 到達城市 3 ,消耗 1 升汽油。
- 代表 2 和代表 3 一起到達城市 1 ,消耗 1 升汽油。
- 代表 2 和代表 3 一起到達首都,消耗 1 升汽油。
- 代表 1 直接到達首都,消耗 1 升汽油。
- 代表 5 直接到達首都,消耗 1 升汽油。
- 代表 6 到達城市 4 ,消耗 1 升汽油。
- 代表 4 和代表 6 一起到達首都,消耗 1 升汽油。
最少消耗 7 升汽油。
示例 3:

輸入:roads = [], seats = 1
輸出:0
解釋:沒有代表需要從別的城市到達首都。
提示:
1 <= n <= 105roads.length == n - 1roads[i].length == 20 <= ai, bi < nai != biroads表示一棵合法的樹。1 <= seats <= 105
理解題目
- 這個問題可以使用圖的廣度優先搜索(BFS)算法來解決。
- 廣度優先搜索(BFS)算法是一種用于遍歷或搜索樹或圖的算法。它從根節點開始,然后訪問所有相鄰的節點,然后再訪問這些相鄰節點的相鄰節點,依此類推。
- 首先,我們需要創建一個鄰接表來表示城市之間的道路關系。
- 然后,從首都開始進行BFS搜索,每次搜索時,將當前城市的汽油消耗累加到總油耗中,并更新每個城市的汽油消耗。
- 最后,返回到達首都的總油耗。
代碼思路
-
它包含一個名為minimumFuelCost的方法,該方法接受兩個參數:roads和seats。**roads是一個二維列表,表示城市之間的道路關系;seats是一個整數,表示每輛車的座位數。**方法的目的是計算到達首都所需的最少汽油量。
? (該函數:
minimumFuelCost是函數名;?
self是類實例的引用,表示這個函數是一個類的方法;?
(self, roads: List[List[int]], seats: int)是函數的參數列表,包括兩個參數:? 一個是
roads,類型為List[List[int]],表示一個二維整數列表;? 另一個是
seats,類型為int,表示一個整數。?
-> int表示這個函數的返回值類型是整數。)def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int: -
首先,代碼創建了一個名為g的空列表,用于存儲道路關系。然后,遍歷roads列表,將每個城市的鄰居添加到g中。
(
[[] for i in range(len(roads) + 1)]表示創建一個長度為len(roads) + 1的列表;? 其中每個元素都是一個空列表。
? 這樣做的目的是為了讓每個節點都有一個與之對應的鄰接表,
? 方便后續進行圖的遍歷和操作。)
# 創建一個空的鄰接表g,用于存儲道路關系g = [[] for i in range(len(roads) + 1)]for e in roads:# 將道路的兩個端點添加到對方的鄰接表中g[e[0]].append(e[1])g[e[1]].append(e[0])res = 0 # 初始化結果變量為0 -
接下來,定義了一個名為dfs的內部函數,用于深度優先搜索。這個函數接受兩個參數:**cur表示當前城市,fa表示當前城市的父節點。**在dfs函數中,首先初始化一個名為peopleSum的變量,表示當前城市及其代表的人數之和。
def dfs(cur, fa):nonlocal res # 聲明res為非局部變量,以便在dfs函數中修改它peopleSum = 1 # 初始化當前節點的人數為1 -
然后,遍歷當前城市的代表,如果代表不是父節點,則遞歸調用dfs函數,并將返回的人數累加到peopleSum中。同時,更新res變量,將其加上(peopleCnt + seats - 1) // seats的結果。最后,返回peopleSum。
for ne in g[cur]: # 遍歷當前節點的所有代表if ne != fa: # 如果代表不是父節點peopleCnt = dfs(ne, cur) # 遞歸調用dfs函數,計算代表的人數peopleSum += peopleCnt # 累加代表的人數到當前節點的人數res += (peopleCnt + seats - 1) // seats # 更新結果變量,計算所需的汽油量return peopleSum # 返回當前節點的人數 -
在主函數中,調用dfs函數,傳入初始值0和-1。最后,返回res作為結果。
dfs(0, -1) # 從根節點開始調用dfs函數return res # 返回結果變量
參考代碼
class Solution:def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:g = [[] for i in range(len(roads) + 1)]for e in roads:g[e[0]].append(e[1])g[e[1]].append(e[0])res = 0def dfs(cur, fa):nonlocal respeopleSum = 1 for ne in g[cur]:if ne != fa:peopleCnt = dfs(ne, cur)peopleSum += peopleCntres += (peopleCnt + seats - 1) // seatsreturn peopleSumdfs(0, -1)return res

)
















