不變因子 初等因子 行列式因子 smith標準型

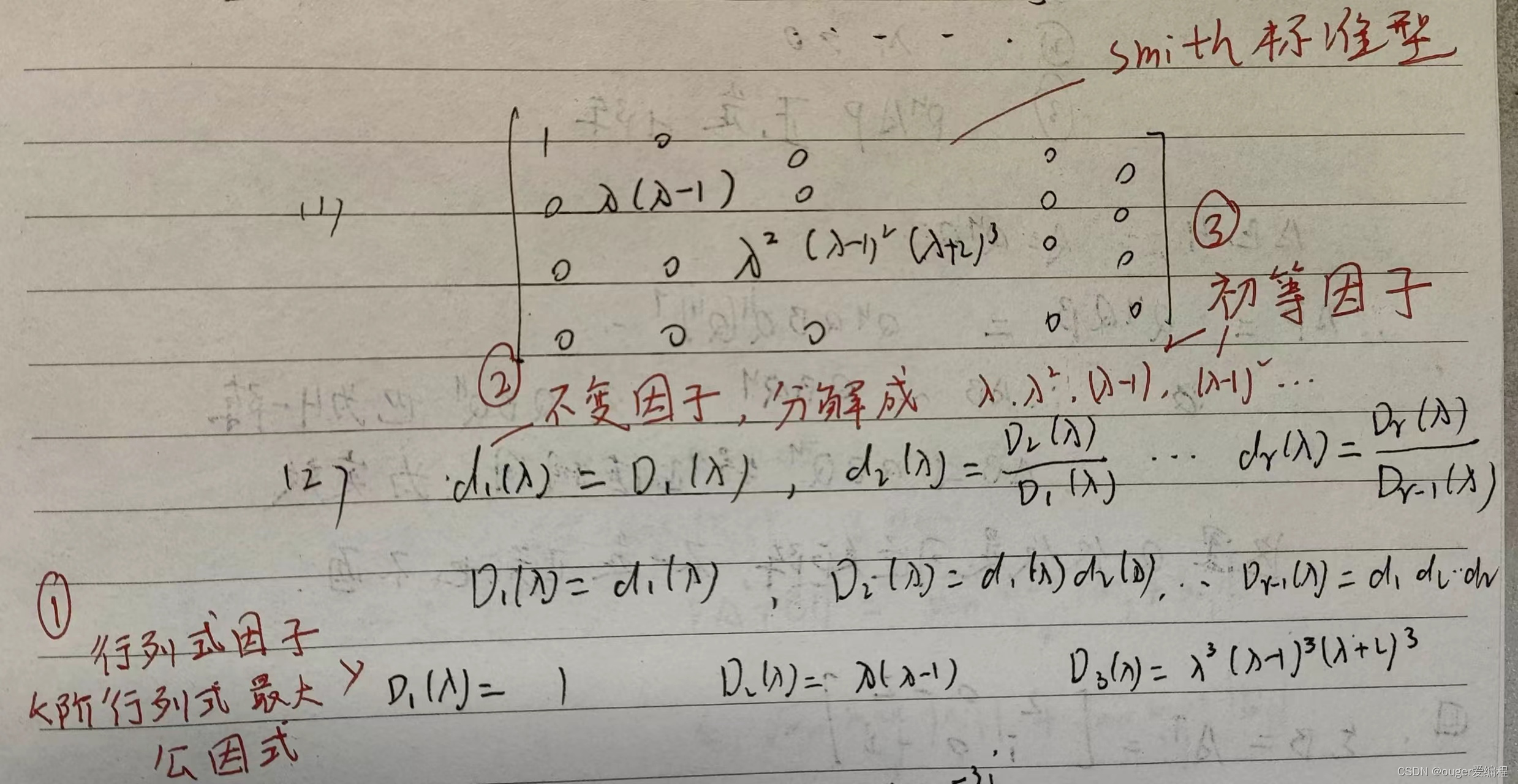
酉矩陣 H-陣等等

$A^H=A$ 就是 H-陣

正定H陣的性質

若 $A$ 為正定的H-陣.

1. 存在可逆矩陣 $Q$， 使得 $A=Q^{H}Q$.
2. 存在$P$, 使得$P^{H}AP=I$.
3. A的特征值大于0.
4. $Q^{?1}AQ$ 也是正定H-陣.

schmidt正交化

$[{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n]$，需要將其正交化，計算過程如下：
$$\begin{array}{rl}{\beta }_1& ={\alpha }_1\\ {\beta }_2& ={\alpha }_2?\frac{({\alpha }_2,{\beta }_1)}{({\beta }_1,{\beta }_1)}{\beta }_1\\ ?& \\ {\beta }_i& ={\alpha }_i?\frac{({\alpha }_i,{\beta }_1)}{({\beta }_1,{\beta }_1)}{\beta }_1?\frac{({\alpha }_i,{\beta }_2)}{({\beta }_2,{\beta }_2)}{\beta }_2???\frac{({\alpha }_i,{\beta }_{i?1})}{({\beta }_{i?1},{\beta }_{i?1})}{\beta }_{i?1}\end{array}$$

投影變換

例題：已知$R^3$ 中向量 $a=(1,0,0)$ ，$\beta =(2,0,3)$，則向量 $x=(x_1,x_2,x_3)\in R^3$ 在子空間 s p a n { α , β } span\{\alpha,\beta\} span{α,β} 上的正交投影為？
先將 α , β 標準正交化 為 η 1 = [ 1 , 0 , 0 ] T , η 2 = [ 0 , 0 , 1 ] T U = [ η 1 , η 2 ] 投影算子 P = U U H 向量 x = ( x 1 , x 2 , x 3 ) ∈ R 3 在子空間 s p a n { α , β } 上的正交投影為： P x = U U H x = [ 1 0 0 0 0 1 ] [ 1 0 0 0 0 1 ] [ x 1 , x 2 , x 3 ] T = [ 1 0 0 0 0 0 0 0 1 ] [ x 1 , x 2 , x 3 ] T = ( x 1 , 0 , x 3 ) \begin{aligned} 先將\alpha, \beta \boldsymbol{標準正交化}為\eta_1&=[1,0,0]^T, \eta_2=[0,0,1]^T\\ U &= [\eta_1, \eta_2] \\ \boldsymbol{投影算子}& \boldsymbol{P=UU^H} \\ 向量 x=(x_1,x_2,x_3 )\in{R^3} &在子空間span\{\alpha,\beta\} 上的正交投影為：\\ Px&=UU^Hx\\ &= { \left [ \begin {matrix} 1 & 0 \\ 0 & 0 \\ 0 & 1 \end {matrix} \right ] } { \left [ \begin {matrix} 1 & 0 & 0\\ 0 & 0 & 1\\ \end {matrix} \right ] } { [x_1,x_2,x_3]^T } \\&= \left[ \begin{matrix} 1 & 0&0 \\ 0 & 0 &0\\ 0 & 0 &1\\ \end{matrix} \right ] [x_1,x_2,x_3]^T \\&= (x_1,0,x_3) \end{aligned} 先將α,β標準正交化為η1?U投影算子向量x=(x1?,x2?,x3?)∈R3Px?=[1,0,0]T,η2?=[0,0,1]T=[η1?,η2?]P=UUH在子空間span{α,β}上的正交投影為：=UUHx= ?100?001? ?[10?00?01?][x1?,x2?,x3?]T= ?100?000?001? ?[x1?,x2?,x3?]T=(x1?,0,x3?)?

矩陣分解

奇異值分解

ref

譜分解

要求$A$ 為正規矩陣，即$A^{H}A=A{A}^H$
$$\begin{array}{rl}A& =[{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n]\left[\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & ?& \\ & & & {\lambda }_n\end{array}\right]\left[\begin{array}{c}{\alpha }_1^H\\ {\alpha }_2^H\\ ?\\ {\alpha }_n^H\end{array}\right]\\ & ={\lambda }_1{\alpha }_1{\alpha }_1^H+{\lambda }_2{\alpha }_2{\alpha }_2^H+?+{\lambda }_n{\alpha }_n{\alpha }_n^H\\ & =\sum _{i=1}^r{\lambda }_i\sum _{j=1}^{n_i}{\alpha }_{ij}{\alpha }_{ij}^H\\ & =\sum {\lambda }_i{G}_i\end{array}\text{\hspace{1em}?}$$

正交三角分解（UR分解）

范數

向量范數

矩陣范數

矩陣函數

一 用 Jordan 標準型和相似變換矩陣 P 來求

二 用最小多項式 $m(\lambda )$來求

函數矩陣

會求導積分就行。