Private Set Intersection from Pseudorandom CorrelationGenerators 最快PSI！導覽解讀

一、概述

二、相關介紹

三、性能對比

四、技術細節

1.KKRT

2.Pseudorandom Correlation Generators

3.A New sVOLE-Based BaRK-OPRF

4.BaRK-OPRF

五、總結

參考文獻

一、概述

????????這篇文章的主要脈絡和核心思想是探討如何利用偽隨機相關生成器（PCG）改進私有集合交（PSI）協議。文章首先介紹了PCG的概念和作用，然后闡述了如何將PCG與分布式密鑰生成協議相結合，以實現長偽隨機相關性的高效生成。接著，文章重點討論了PCG對私有集合交協議的改進作用，提出了兩個主要結果：高度優化的半誠實PSI協議和利用PCG實現新相關性的協議。這些結果展示了PCG在安全計算應用中的潛在價值，為提高協議效率和性能提供了新的思路和方法。

????????這篇文章的突破包括： 1. 針對私有集合交（PSI）協議，提出了高度優化的半誠實PSI協議，實現了競爭性的通信和顯著的性能改進。 2. 利用PCG實現新相關性的協議，在標準模型下實現了全面的惡意安全性，且在通信和性能方面具有競爭優勢。 3. 發現了Cuckoo hashing-based協議在PCG方面的優勢，以及對KKRT協議的深入優化，使得通信復雜度完全獨立于計算安全參數，為協議的進一步優化提供了新的可能性。這些突破為安全計算應用中的私有集合交協議帶來了新的發展方向和性能提升。

二、相關介紹

? ? ? ? 目前主流的實現隱私求交PSI的關鍵技術包括：Key exchange-based、Cuckoo hashing-based、OKVS、Polynomial manipulation.

????????其中，基于密鑰交換的早期PSI協議使用Diffie-Hellman密鑰交換技術，通信復雜度相對較低，但需要為每個項目計算多個指數，性能相對較差。基于Cuckoo哈希的PSI協議是過去幾十年中最常用的PSI協議之一，通常與快速的無意識傳輸擴展相結合。最近，基于OKVS的PSI協議已經超越了基于Cuckoo哈希的協議，但是KKRT協議仍然是最具競爭力的PSI協議之一。基于多項式操作的PSI協議將數據集表示為有限域上的多項式，并通過對這些多項式進行操作來計算集合操作。雖然這些協議通常比基于Cuckoo哈希或OKVS的協議慢得多，但它們具有一些優點，例如實現更強的功能（如閾值私有集合交[GS19]）并在標準模型下提供安全性。

? ? ? ? 當然還有文章的“主角”：seudorandom correlation generators.在現代安全計算協議中，安全共享相關隨機字符串是一個關鍵組成部分，PCG可以在幾乎沒有通信的情況下實現這個功能。PCG還可以用于構建無聲無意識傳輸擴展協議，這些協議可以使用最小的（對數級別的）通信實現（偽隨機）OT擴展。由于最高效的PSI協議依賴于高效的OT擴展，因此使用基于PCG的技術來提高其效率是一個自然的想法。最近，這種方法已經在基于OKVS的PSI協議中得到了應用，導致了迄今為止最有效的PSI協議[RS21]。基于OKVS的PSI協議現在已經牢固地確立為該領域的主導范式，使用PCG來進一步減少其通信開銷似乎進一步擴大了與其他范式之間的差距。

三、性能對比

四、技術細節

1.BaRK-OPRF

這里Alice將獲得所有數據偽隨機數，并且Bob將獲得所有種子。上面這個協議若基于OTE將十分高效的實踐，但是當其應用到隱私求交時，我們需要注意Bob會將所有數據計算對應的偽隨機函數并發送給Alice，其中的傳輸量將與Bob的數據量相關。當Bob的數據量較大時，需要發送整個數據集給Alice，傳輸開銷“難以接受”。

引入Cuckoo Hash見小通信和計算開銷

為了獲得PSI協議，KKRT使用哈希將數據集映射到桶中。使用簡單的哈希策略，對于大小為n的數據集，每個桶中最多只能有log n / log log n個項，這仍會導致顯著的開銷，因為必須比較同一桶中Alice和Bob的所有項對。

2.Pseudorandom Correlation Generators

PCG 是近年 MPC 研究的熱點，它的本質是通過“短的種子”生成“長的隨機串”（即相關隨機數）。而在 MPC 應用中，“離線”階段不再需要存儲大量的相關隨機數，而只需要存儲少量的 PCG 種子。當“在線”階段需要消耗相關隨機數時，各方不需要任何交互，可以直接通過 PCG 種子產生所需的相關隨機數。

兩方的偽隨機相關生成器由 PCG.Gen 和 PCG.Extend 兩個算法構成，其中 PCG.Gen 可以由可信第三方或兩方協議實現 [BCGI18][BCG+19b]。

?● 隨機算法，給定安全參數，輸出一對種子。

?● 確定性算法，給定 ?及種子，輸出偽隨機串，并且滿足。

3.vector OLE

看圖中實現的效果，Alice將獲得u和v，Bob將獲得?和w，并滿足最后的條件。本文的將要使用vole代替oprf，或者說使用vole版的oprf。w、v、u均為向量。

Alice發送z=x-u給Bob，并且自身計算 H(i,v_i) 即可，

Bob計算(k1, · · · , kn) = ? · z + w， $F_{\Delta, k_i}(y)=H(i, k_i-\Delta y)$ 。

正確性驗證：

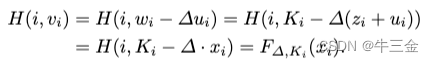
為什么使用VOLE實現OPRF。

1. 高效性：VOLE協議可以高效地生成偽隨機相關性，這對于實現OPRF協議是非常重要的。通過使用VOLE，可以在保持安全性的同時，實現高效的協議，這對于實際應用中的性能至關重要。近年來VOLE非常火熱的安全協議，將帶來效率的大幅度提升。
2. 隱私保護：VOLE協議允許兩方計算他們的輸入的線性函數，同時不泄露有關輸入的任何信息。這種隱私保護特性對于構建安全的OPRF協議至關重要，因為它確保了參與方的輸入保持私密。
3. 安全性：VOLE協議提供了安全的計算環境，確保了計算的正確性和隱私性。這對于構建安全的OPRF協議是至關重要的，因為OPRF協議需要在不暴露輸入的情況下進行計算。因此，使用sVOLE來實現OPRF可以同時保證高效性、隱私保護和安全性，使得OPRF協議在實際應用中更加可行和可靠。

五、總結

本文介紹了向量OLE和sVOLE在實現OPRF協議中的重要性和應用。向量OLE是一種密碼學原語，允許兩個參與方計算它們各自輸入向量的內積，同時不泄露有關它們個體輸入的任何信息。sVOLE是一種基于子域的向量OLE協議，可以高效地生成偽隨機相關性，同時保護參與方的隱私。 OPRF是一種重要的密碼學原語，用于在不暴露輸入的情況下計算偽隨機函數。使用sVOLE來實現OPRF協議可以同時保證高效性、隱私保護和安全性，使得OPRF協議在實際應用中更加可行和可靠。本文還介紹了一些相關的研究成果和技術，包括私有集合交集協議、安全多方計算、Cuckoo hashing-based協議等。這些技術和成果都與向量OLE和sVOLE密切相關，為實現安全、高效的計算提供了重要的支持和保障。總之，向量OLE和sVOLE在實現OPRF協議中具有重要的應用和意義，可以為實現安全、高效的計算提供重要的支持和保障。

參考文獻

相關資料——https://download.csdn.net/download/niujinya/88610168

[BC22]?Private Set Intersection from Pseudorandom Correlation Generators

[GS19]?S. Ghosh and M. Simkin. The communication complexity of threshold private set intersection.In CRYPTO 2019, Part II, LNCS 11693, pages 3–29. Springer, Heidelberg, August 2019.

[RS21]?P. Rindal and P. Schoppmann. VOLE-PSI: Fast OPRF and circuit-PSI from vector-OLE. LNCS,pages 901–930. Springer, Heidelberg, 2021

[KKRT16]?V. Kolesnikov, R. Kumaresan, M. Rosulek, and N. Trieu. Efficient batched oblivious PRF with applications to private set intersection. In ACM CCS 2016, pages 818–829. ACM Press, October 2016.

[KRTW19]?V. Kolesnikov, M. Rosulek, N. Trieu, and X. Wang. Scalable private set union from symmetric-key techniques. In ASIACRYPT 2019, Part II, LNCS 11922, pages 636–666. Springer, Heidelberg, December 2019.

[CM20]?M. Chase and P. Miao. Private set intersection in the internet setting from lightweight oblivious PRF. In CRYPTO 2020, Part III, LNCS 12172, pages 34–63. Springer, Heidelberg, August 2020.

[PRTY20]?B. Pinkas, M. Rosulek, N. Trieu, and A. Yanai. PSI from PaXoS: Fast, malicious private set intersection. In EUROCRYPT 2020, Part II, LNCS 12106, pages 739–767. Springer, Heidelberg, May 2020.

[GPR+21]?G. Garimella, B. Pinkas, M. Rosulek, N. Trieu, and A. Yanai. Oblivious key-value stores and amplification for private set intersection. LNCS, pages 395–425. Springer, Heidelberg, 2021.

[CRR21]?G. Couteau, P. Rindal, and S. Raghuraman. Silver: Silent VOLE and oblivious transfer from hardness of decoding structured LDPC codes. LNCS, pages 502–534. Springer, Heidelberg, 2021.