---

前言——TSNE是t-Distributed Stochastic Neighbor Embedding的縮寫

TSNE是t-Distributed Stochastic Neighbor Embedding的縮寫,它是一個非線性降維算法。

TSNE的主要作用和優點如下:

• 將高維數據投影到低維空間,如二維或三維,實現高維數據的可視化。

• 相比其他降維方法如PCA,TSNE在保留局部結構信息上的效果更好,尤其適用于高維稠密數據。

• 它可以很好地區分數據中的簇結構,有利于觀察不同類別或類型的數據分布情況。

1、可運行的T-SNE程序

from sklearn.datasets import load_iris
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
import matplotlib
matplotlib.use('TkAgg')# 加載數據
iris = load_iris()
X = iris.data
y = iris.target# TSNE降維
tsne = TSNE(n_components=2, random_state=0)
X_tsne = tsne.fit_transform(X)# 繪制點
plt.scatter(X_tsne[:,0], X_tsne[:,1], c=y, marker='o', s=5)# 添加圖例
plt.legend(iris.target_names)# 添加標題
plt.title("TSNE projection of the Iris dataset")plt.show()

2. 實驗結果

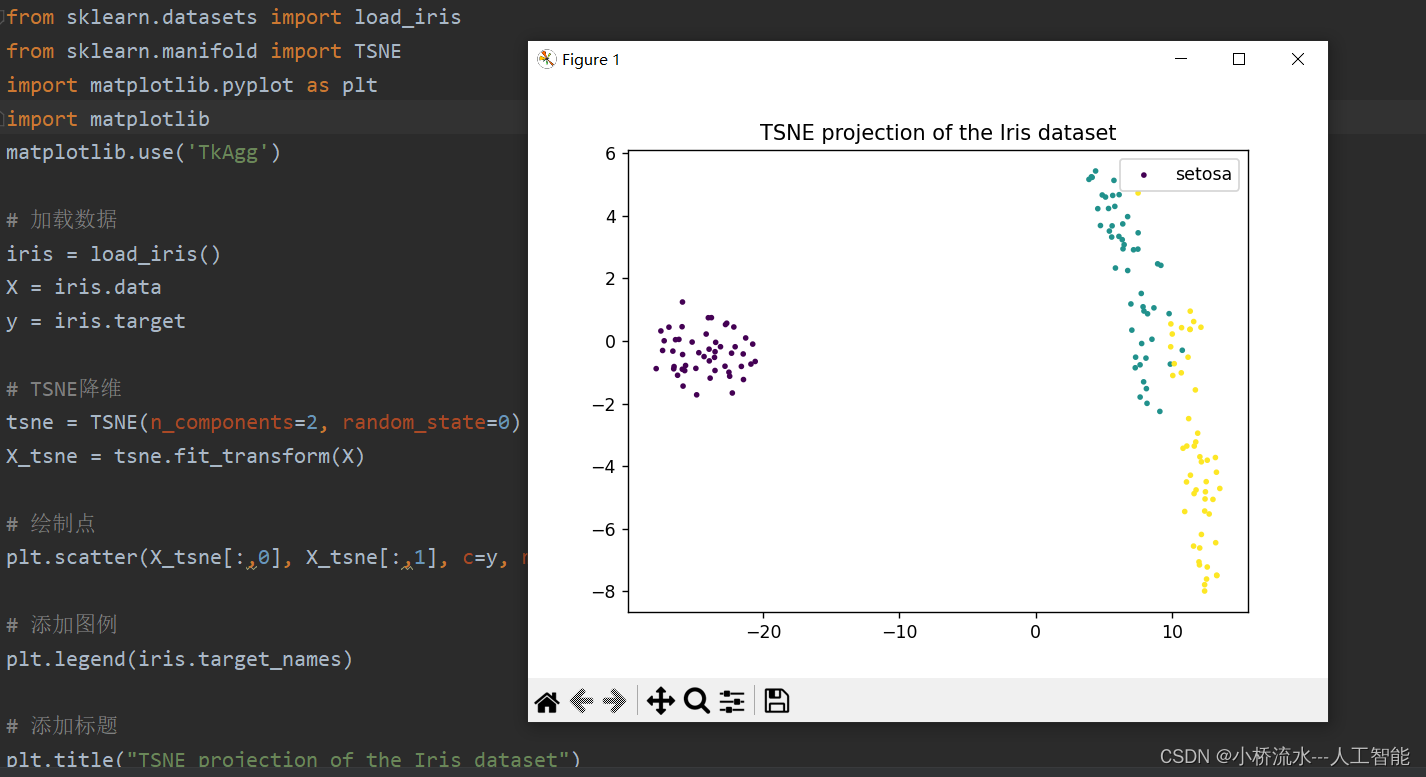
3、針對上述程序我們詳細分析T-SNE的使用方法

3.1 加載數據

• load_iris()函數從sklearn.datasets模塊加載鳶尾花數據集,
• iris包含數據集的特征數據X和標簽數據y。

3.2 TSNE降維

• TSNE是一種非線性降維算法,用于高維數據的可視化。它可以將高維數據投影到二維或三維空間。

• TSNE(n_components=2)實例化一個TSNE模型,降維后的維度數設為2。

• random_state=0固定隨機數種子,使得結果可重復。

• fit_transform(X)對特征數據X進行降維,返回降維后的新特征X_tsne。

3.3 繪制點

• X_tsne包含每個樣本的二維坐標。

• plt.scatter以(x,y)坐標方式繪制每個點,c=y指定點的顏色。

• marker='o’設置點的形狀為圓形。

• s=5控制點的大小。

通過TSNE降維,高維數據X被投影到二維空間,得到低維表示X_tsne。然后根據X_tsne和y進行散點圖繪制,就可以實現TSNE降維結果的可視化。這是TSNE的標準流程。

3.4 關于顏色設置，顏色使用的標簽數據的說明c=y

c=y這行代碼的含義和作用是:

• c參數用于設置散點圖中每個點的顏色。

• y變量包含了樣本的類別標簽信息。對于鳶尾花數據集來說,y取值為0、1或2,分別表示三種花的類別。

• 當我們設置c=y時,就是根據每個樣本在y中的類別標簽值,來動態設置這個樣本點在散點圖中的顏色。

• 具體來說:

  • 如果一個樣本的y值為0,那么這個點的顏色就會取顏色映射中的第一個顏色。

  • 如果y值為1,點顏色取第二個顏色。

  • 如果y值為2,點顏色取第三個顏色。

• 這樣每個類別的樣本點就會使用不同的顏色來繪制,從而在可視化結果中清晰區分開各個類別。

---

總結

• 在科研中,TSNE廣泛應用于圖像分類、自然語言處理等領域的數據降維和可視化。

• 比如對神經網絡分類結果進行TSNE降維,可以觀察不同類別樣本在特征空間中的分布,有助于分析模型表現。

• 對文本語料進行TSNE降維,可以觀察詞匯在語義空間中的分布,幫助理解語義結構。

• 對單細胞RNA-seq數據進行TSNE降維,可以觀察不同類型細胞在表達空間中的分布,有助于發現新型細胞亞群。

所以總體來說,TSNE通過高效的降維和保留局部結構,有助于科研人員直觀觀察高維數據的內在結構,分析模型效果,發現數據中的新知識,從而推動科研工作的進展。它為數據可視化和理解提供了重要的工具支持。