目錄
- 前言
- 遞歸
- 定義
- 遞歸的兩個必要條件
- 接受一個整型值(無符號),按照順序打印它的每一位
- 使用函數不允許創建臨時變量,求字符串“abcd”的長度
- 求n的階乘
- 求第n個斐波那契數
- 迭代
- 總結
- 遞歸與迭代的主要區別
- 用法不同
- 結構不同
- 時間開銷不同
- 兩個經典問題
前言
從前有座山,山里有座廟,廟里有個老和尚,正在給小和尚講故事!故事是什么?“從前有座山,山里有座廟,廟里有個老和尚,正在給小和尚講故事!故事是什么?‘從前有座山,山里有座廟,廟里有個老和尚,正在給小和尚講故事!故事是什么?……’”
遞歸
定義
計算機科學中,遞歸是是指在函數的定義中使用函數自身的方法。它通常把一個大型的復雜問題層層轉化為一個與原問題相似的規模較小的問題來求解,遞歸只需要少量的代碼就可以描述出解題過程中的多次重復計算,大大減少了程序的代碼量。
遞歸的主要思想是:大化小
遞歸的兩個必要條件
1.存在限制條件,當滿足這個限制條件時,遞歸停止。
2.每次遞歸調用之后越來越接近限制條件。
錯誤示例:
#include<stdio.h>int main()
{printf("hello world!\n");main();return 0;
}
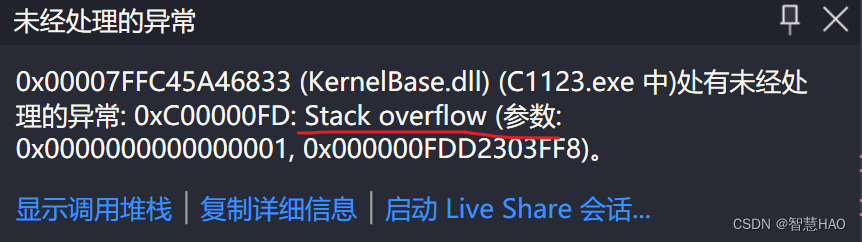
畫紅線的地方,意思是棧溢出,從上面寫的程序中發現,遞歸沒有停止的限制條件,導致死遞歸。
接受一個整型值(無符號),按照順序打印它的每一位
示例1:
問題描述:
接受一個整型值(無符號),按照順序打印它的每一位。
樣例輸入:1234
樣例輸出:1 2 3 4
代碼示范:
#include<stdio.h>void Func(unsigned int x)
{if (x > 9){Func(x / 10);}printf("%d ", x % 10);
}
int main()
{unsigned int num = 0;scanf("%d", &num); //假設輸入的是123Func(num);return 0;
}
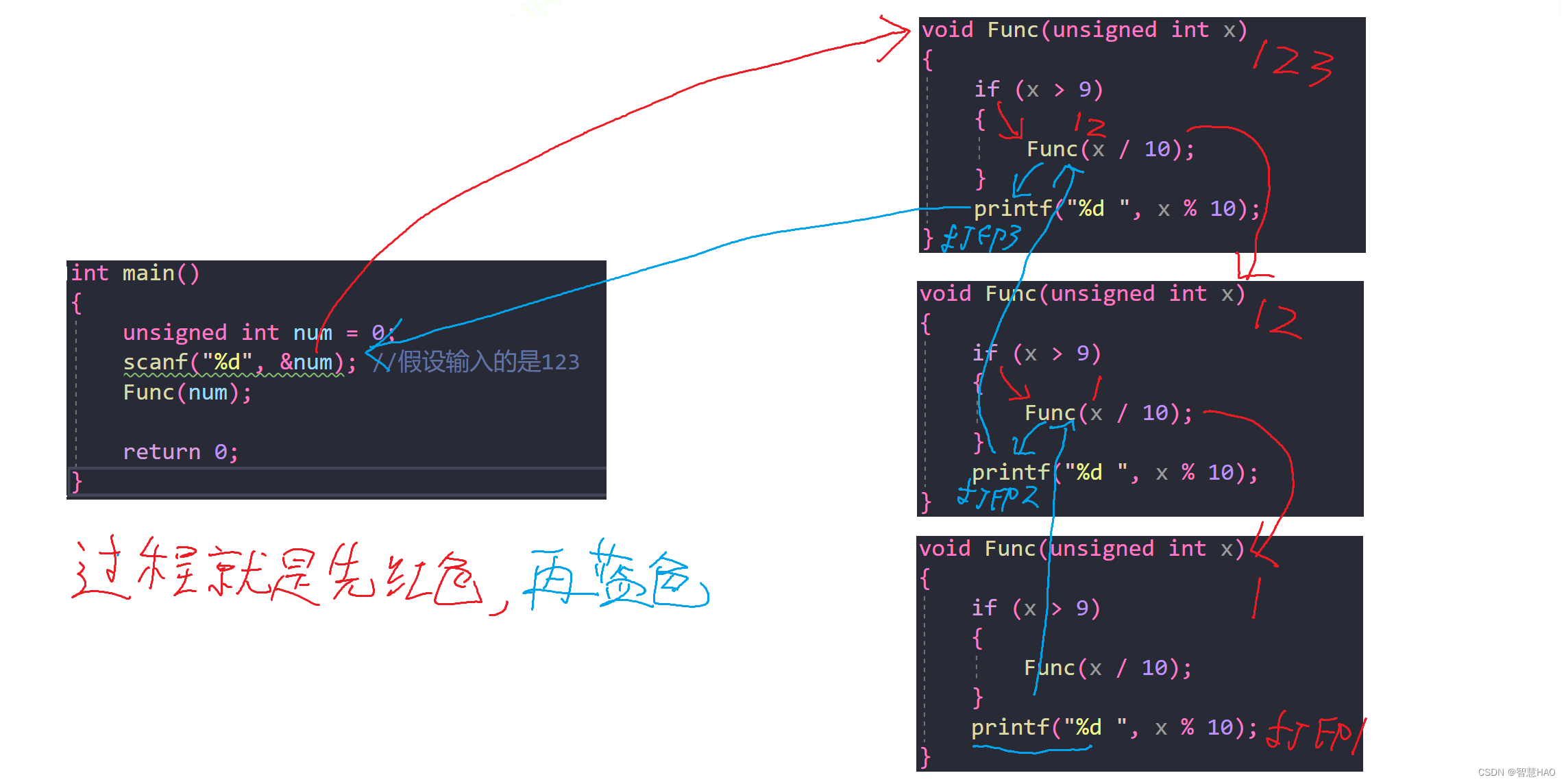
到這里對遞歸應該有一個比較清晰的認識了,在圖中紅色過程表示的就是遞歸當中的“遞”,藍色過程表示的就是遞歸當中的“歸”。
使用函數不允許創建臨時變量,求字符串“abcd”的長度
示例2:
問題描述:
使用函數不允許創建臨時變量,求字符串“abcd”的長度
分析: 直接求字符串“abcd”的長度,它是字符串,在前面文章中說過字符串的結束標志是 \0
代碼展示:
#include<stdio.h>
#include<string.h>int Length(char* l)
{int count = 0;while (*l != '\0'){count++;l++;}return count;
}
int main()
{char arr[] = "abcd";int len = Length(arr);printf("%d\n", len);return 0;
}
這段代碼完全沒有問題,但是題目要求不允許創建臨時變量,這里創建了臨時變量count。
再分析:
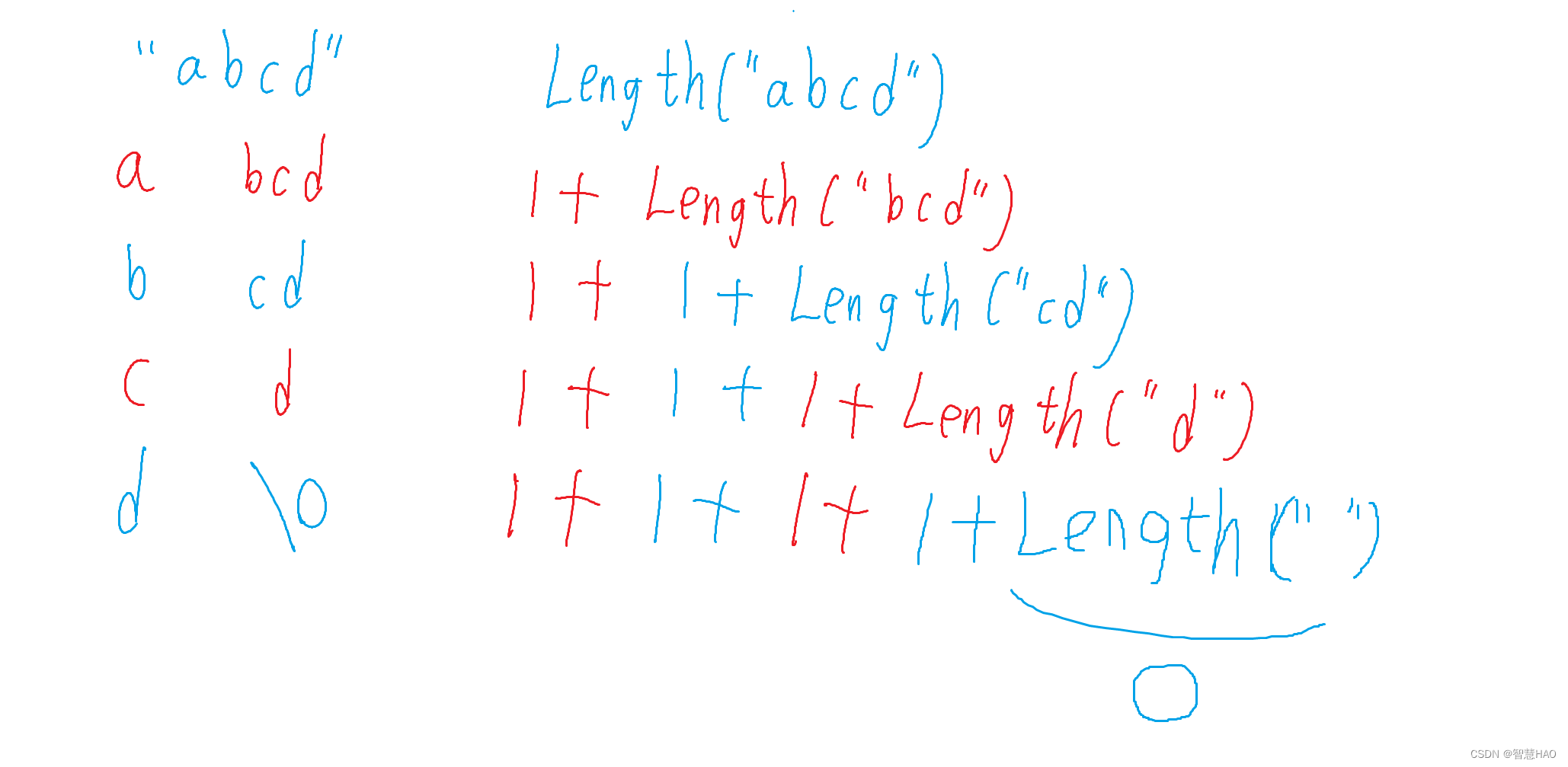
所以我們可以將Length函數寫成遞歸的形式:
//遞歸
int Length(char* length)
{if (*length == '\0')return 0;elsereturn 1 + Length(length + 1);
}
我們再分析過程:

求n的階乘
我們回顧一下n!怎么算:
#include<stdio.h>int Func(int x)
{int i = 0;int j = 1;for (i = 1; i <= x; i++){j *= i;}return j;
}
int main()
{int n = 0;scanf("%d", &n);int result = Func(n);printf("%d\n", result);return 0;
}
上述代碼是非遞歸的形式,我們再來思考一下如何使用遞歸來寫n!:
我們可以發現n!=n*(n-1)!
所以Func函數可以寫成:
int Func(int x)
{if (x <= 1)return 1;else return x * Func(x - 1);
}
求第n個斐波那契數
斐波那契數列由0和1開始,之后的斐波那契數就是由之前的兩數相加而得出。
前幾個斐波那契數是:
1、 1、 2、 3、 5、 8、 13、 21、 34、 55、 89、 144……
也就是說從第三個數開始,后面的每一個斐波那契數都是前兩個數的和。
到這里就可以直接寫代碼了:
#include<stdio.h>int Fib(int n)
{if (n <= 2)return 1;elsereturn Fib(n - 1) + Fib(n - 2);
}
int main()
{int n = 0;scanf("%d", &n);int result = Fib(n);printf("%d\n", result);return 0;
}
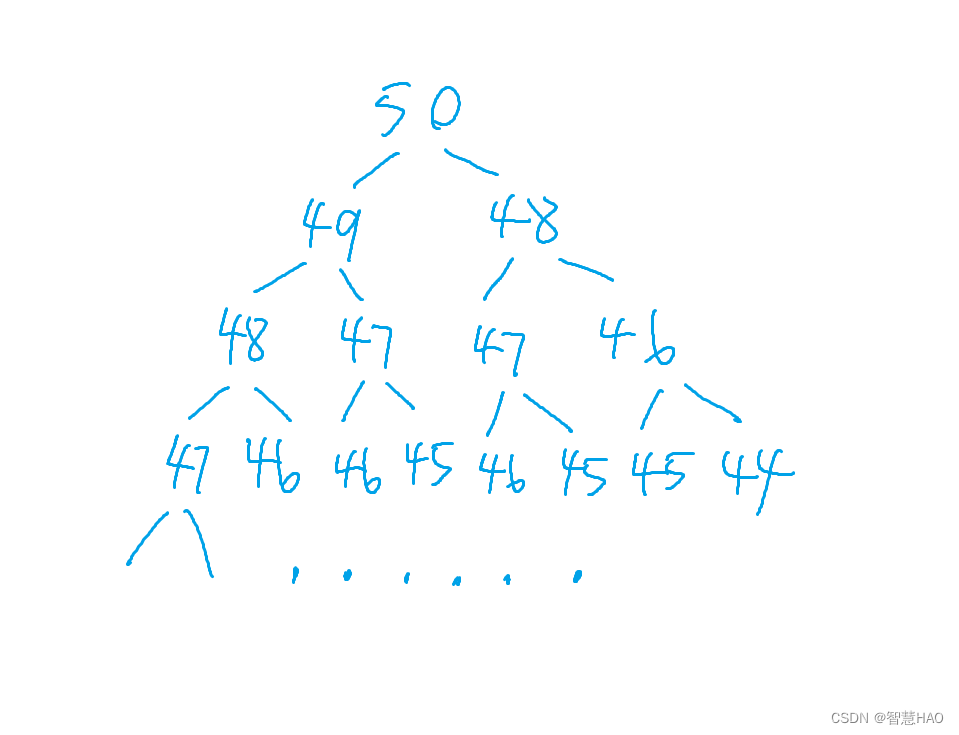
這時候我們信心滿滿,讓計算機幫我求第50個斐波那契數,當我們執行程序后在鍵盤輸入50,卻發現,等了很久都沒有發現它輸出內容。
為什么?
我們要求第50個斐波那契數,就需要計算第49個和第48個數,計算第49個數又需要計算第48個數和第47個數,可以想一下上面這個圖畫到末端需要畫多少,除了前兩個數,要算2的48次方,而int型只占4個字節的內存,也就是32位,2的32次方都已經42億多,可想而知計算量非常龐大。按照遞歸的方式要進行大量的重復計算。我們可以做一個計數,計算第40個斐波那契數中3被計算了多少次,你會發現3被計算了將近四千萬次,效率非常低。所以不是因為計算機偷懶沒算,它也在拼命地計算,只是量太大,它一會兒也算不出來。
那么應該如何改進呢?
迭代
在計算機科學中,迭代是程序中對一組指令(或一定步驟)的重復。它既可以被用作通用的術語(與“重復”同義),也可以用來描述一種特定形式的具有可變狀態的重復。可以簡單理解為普通循環。但與普通循環有所差別,迭代時,循環代碼中參與運算的變量同時是保存結果的變量,當前保存的結果作為下一次循環計算的初始值
我們知道函數形參是被存放在棧區當中,遞歸每“遞”一次,就要開辟一個變量的內存,那么當參數非常大的時候,棧區內存不夠了,棧區放不下了,也就是說棧區空間已經被耗盡了,但是你的東西還沒放完,這個時候就會出現棧溢出的現象。
那么我們回頭再看求第n個斐波那契數,能否將遞歸轉換成迭代的形式。
while (n >= 3){c = a + b;a = b;b = c;n--;}return c;
那么當n小于3的時候,也就是第1個或者第2個數,都是1,所以在給a,b,c初始化的時候,都賦值為1即可。
完整代碼:
#include<stdio.h>
//迭代
int Fib(int n)
{int a = 1;int b = 1;int c = 1;while (n >= 3){c = a + b;a = b;b = c;n--;}return c;
}
int main()
{int n = 0;scanf("%d", &n);int result = Fib(n);printf("%d\n", result);return 0;
}
這個時候程序運行后輸入50,盡管結果仍然是錯誤的,但是速度非常快。解決了大量重復計算的問題。
總結
當使用遞歸可能會導致棧溢出時,程序效率明顯下降的時候,就不能夠使用遞歸了。
如何解決?
1.可以使用迭代替換遞歸。
2.在遞歸函數設計中可以使用static限制變量,讓變量申請一塊內存后,在那一塊內存折騰。不僅不再大量開辟棧區內存,從而導致棧溢出,并且static可以保存遞歸時的中間狀態,并且為各個調用層所訪問。
- 遞歸代碼量少,迭代不易想到,遞歸比迭代更清晰。所以許多問題采用遞歸的方式解釋。
- 迭代實現比遞歸實現的代碼可讀性差,但是效率高。
- 當問題復雜的時候,難以用迭代實現,此時使用遞歸會更加簡潔。
遞歸與迭代的主要區別
用法不同
- 迭代是代碼塊的重復。雖然需要更多的代碼,但時間復雜度通常小于遞歸的時間復雜度。
- 遞歸是多次調用自身,因此代碼長度非常小。但是,當有非常非常多次的遞歸調用時,遞歸的時間復雜度可能會呈指數級增長。
結構不同
- 迭代是環結構,從初始狀態開始,每次迭代都遍歷這個環,并更新狀態,多次迭代直到到達結束狀態。
- 遞歸是樹結構,從字面可以理解為重復“遞”和“歸”的過程,當“遞”到達底部時就會開始“歸”。
時間開銷不同
- 與迭代相比,遞歸具有大量的開銷。遞歸具有重復函數調用的開銷,即由于重復調用同一函數,代碼的時間復雜度增加了許多倍。
兩個經典問題
- 漢諾塔問題
- 青蛙跳臺階問題
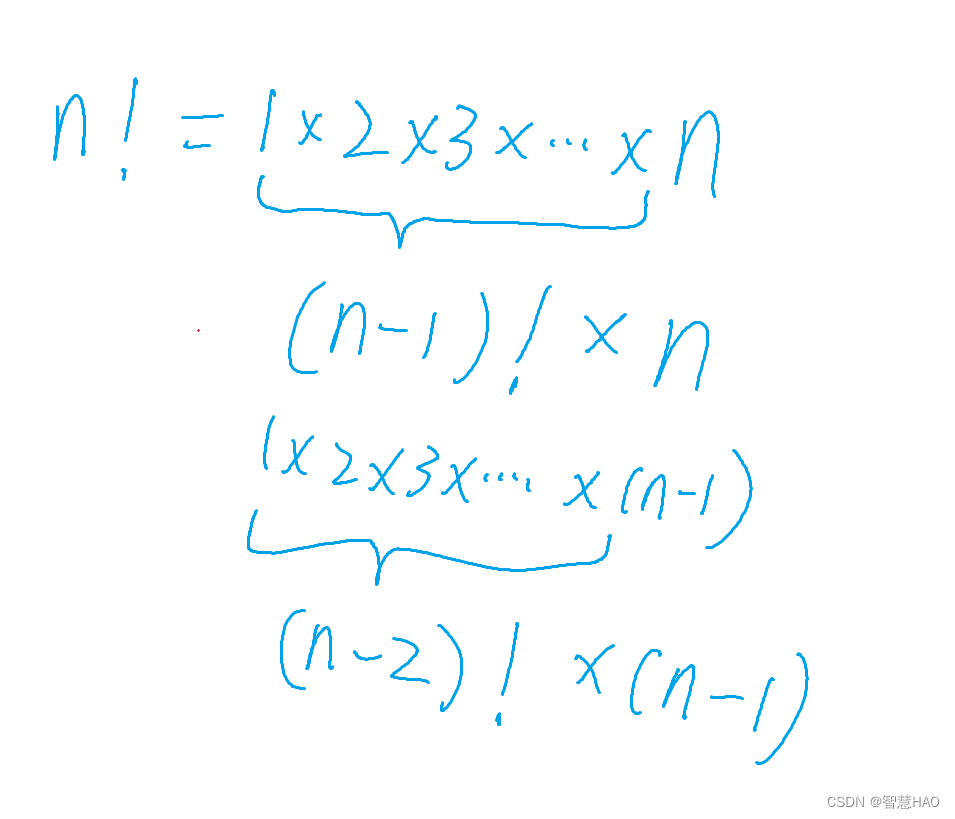
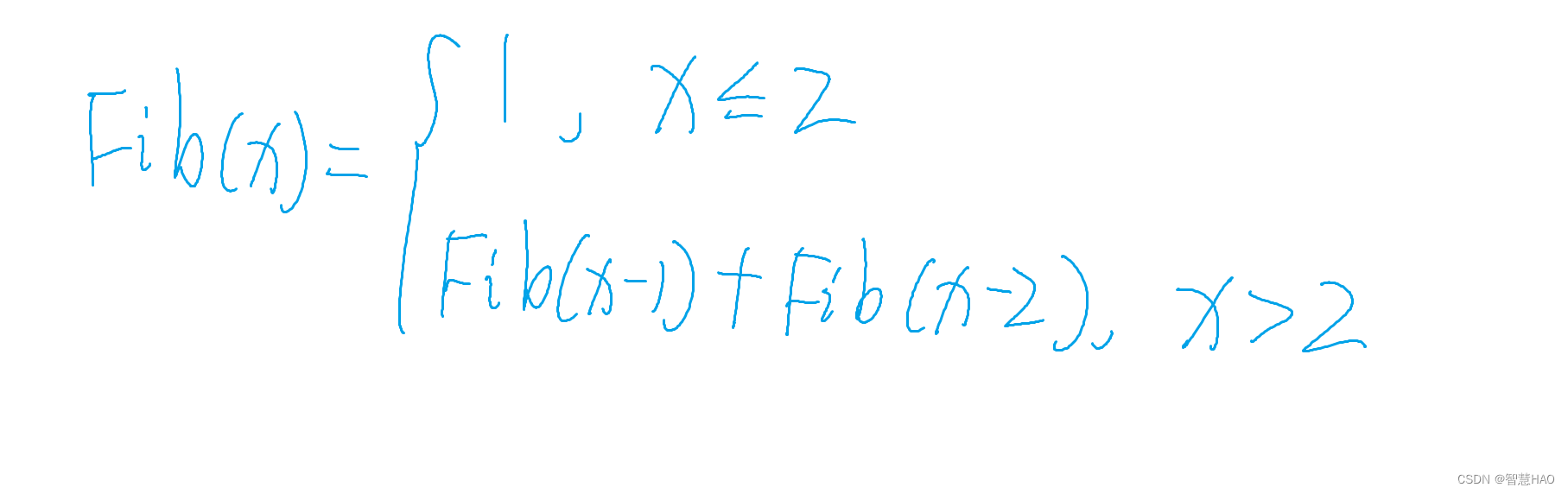




)


)






——算術運算符)

)



