目錄
1 基本概念
結構體定義
各種接口
2?二叉排序樹的構建和中序遍歷
遞歸版單次插入
非遞歸版單次插入
3?二叉排序樹的查找
非遞歸版本
遞歸版本
4?二叉排序樹的刪除(難點)
1 基本概念
????????普通二叉排序樹是一種簡單的數據結構,節點的值根據特定順序(通常是升序或降序)排列。然而,如果普通二叉排序樹不平衡,即左、右子樹的高度相差很大時,查詢效率可能會降低。因此引出了avl樹、紅黑樹等一系列高階數據結構。
? ? ? ?基本性質:
- 若它的左子樹不空,則左子樹上所有結點的值均小于它根結點的值。
- 若它的右子樹不空,則右子樹上所有結點的值均大于它根結點的值。
- 它的左、右子樹均為為?叉排序樹。
- 二叉排序樹的查找時間復雜度為樹的高度,即為O(以2為底N的對數) ,下面全寫成O(logN)
- 二叉排序樹的中序遍歷輸出是一個遞增的數列。
結構體定義
typedef struct BSTreeNode
{int val;struct BSTreeNode* left;struct BSTreeNode* right;
}BSTNode,*BiTree;各種接口
???????
關于用到C++中的引用:
BSTNode是結構體struct BSTNode的別名,BiTree是結構體struct BSTNode指針。
在鏈表中,首次插入時需要修改頭節點,由于頭節點的定義也是一個指針,所以要修改一個一級指針,必須傳入二級指針或者一級指針的引用,二叉樹也是一樣,首次插入需要修改根節點的指向,所以這里用引用,當然也可以用二級指針,嚴蔚敏老師編寫的數據結構中也經常用到C++的引用。
而再次或多次進行插入時,我們用cur去遍歷鏈表或二叉樹,其實是修改鏈表和二叉樹的一個個結構體,這時我們只需要結構體指針,其實就只需要一級指針即可。
因此,我們直接用二級指針或一級指針的引用,就能解決所有的問題。?
2?二叉排序樹的構建和中序遍歷
?構建原則:
①根節點為空,先構建根節點。
②插入節點的值小于根節點的值,去根節點的左子樹尋找插入位置。
③插入節點的值大于根節點的值,去根節點的右子樹尋找插入位置。
void Create(BiTree& root,int* a,int n)
{for (int i = 0; i < n; ++i){BST_InsertR(root, a[i]);//BST_Insert(root, a[i]);}
}遍歷數組O(N),數組每個元素插入O(logN),因此構建的時間復雜度是O(NlogN)。
遞歸版單次插入
int BST_InsertR(BiTree& root, int x)
{//先申請節點BSTNode* newnode = (BiTree)malloc(sizeof(BSTNode));if (newnode == nullptr){perror("malloc fail");exit(-1);}newnode->val = x;newnode->left = newnode->right = nullptr;//進行插入if (root == nullptr)//空樹或者走到空{root = newnode;return 1;//插入成功}if (root->val == x)return -1;//插入失敗,節點元素值不能相同if (root->val > x)//x小于根節點的值,就去左子樹插入return BST_InsertR(root->left, x);if (root->val < x)//x大于于根節點的值,就去右子樹插入return BST_InsertR(root->right, x);
}非遞歸版單次插入
?定義兩個指針,cur和prev,prev指向cur的根節點,cur最后走到空,對prev的左右指針進行操作,比對prev->val和x,如果val<x,就讓prev->right指向新節點,反之。
int BST_Insert(BiTree& root, int x)
{//二叉排序樹左孩子的值比根的值要小,右孩子的值比根的值要大BSTNode* newnode = (BiTree)malloc(sizeof(BSTNode));if (newnode == nullptr){perror("malloc fail");exit(-1);}newnode->val = x;newnode->left = newnode->right = nullptr;//第一次進來root為空if (root == nullptr){root = newnode;return 0;}//第二次開始往后遍歷BSTNode* cur = root;BSTNode* prev = nullptr;while (cur)//讓cur走到空{prev = cur;if (cur->val < x){cur = cur->right;}else if (cur->val > x){cur = cur->left;}else{return -1;//插入失敗,不能有元素相等的情況}}if (prev->val < x){prev->right = newnode;}if (prev->val > x){prev->left = newnode;}return 0;//插入成功
}假設我們用這個數組去構建一棵樹:
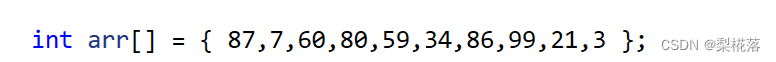
結果是這樣的:

中序遍歷:
void InOrder(BiTree root)
{if (root == nullptr)//空樹或走到空return;InOrder(root->left);//左子樹printf("%d ", root->val);//根InOrder(root->right);//右子樹
}輸出的結果一定是一個遞增序列,因此二叉排序樹的中序遍歷才有意義。
3?二叉排序樹的查找
查找原則:
①所查找的值比當前節點的值要小,就去左子樹找
②所查找的值比當前節點的值要大,就去右子樹找
③查找成功,返回結構體指針BSTNode*/BiTree
二叉排序樹的最大查找次數,就是樹的深度,類似于折半查找,每查一次排除一半的樹。
因此二叉排序樹的查找時間復雜度為O(logN) 。
非遞歸版本
BSTNode* BinarySearch(BiTree root,int x)
{BSTNode* cur = root;while (cur){if (cur->val < x){cur = cur->right;}else if (cur->val > x){cur = cur->left;}else{return cur;}}return nullptr;
}遞歸版本
BSTNode* BinarySearchR(BiTree root, int x)
{if (root == nullptr)//空樹或者找到空了還沒找到return nullptr;if (x == root->val)return root;if (x > root->val)//大于就去右子樹找return BinarySearchR(root->right, x);if(x < root->val)//小于就去左子樹找return BinarySearchR(root->left, x);
}4?二叉排序樹的刪除(難點)
刪除原則:
①刪除節點的右子樹為空,左子樹不為空,把左子樹頂上來。
②刪除節點的左子樹為空,右子樹不為空,把右子樹頂上來。
③刪除節點的左右子樹都不為空,要么在左子樹中找最大的數據和根的數據交換,要么在右子樹中找最小的數據和根的數據交換。
void DeleteNode(BiTree& root, int x)
{if (root == nullptr)//找不到或者根為空,直接返回{return;}//先找后刪除,遞歸if (x < root->val){DeleteNode(root->left, x);}if (x > root->val){DeleteNode(root->right, x);}//找到了,執行刪除if (root->val == x){if (root->left == nullptr)//左子樹為空,把右子樹頂上去{BiTree tmp = root;root = root->right;free(tmp);}else if (root->right == nullptr)//右子樹為空,把左子樹頂上去{BiTree tmp = root;root = root->left;free(tmp);}else//左右子樹均不為空,要么在左子樹中找最大的數據和根的數據交換,要么在右子樹中找最小的數據和根的數據交換//采用前者即可,左子樹的最大數據就是左子樹的最右結點{BiTree left = root->left;while (left->right){left = left->right;}root->val = left->val;//free(left);//不能這么做,萬一這個結點有左子樹怎么辦?//只能重新在T的左子樹找這個結點,復用遞歸刪除這個結點DeleteNode(root->left, left->val);}}
}圖解何為“頂上來”?
由于函數傳參用到引用,因此root就是上一層函數root->left或者root->right的別名:

定義指針tmp去指向root形參,root形參用root(1)表示一下:
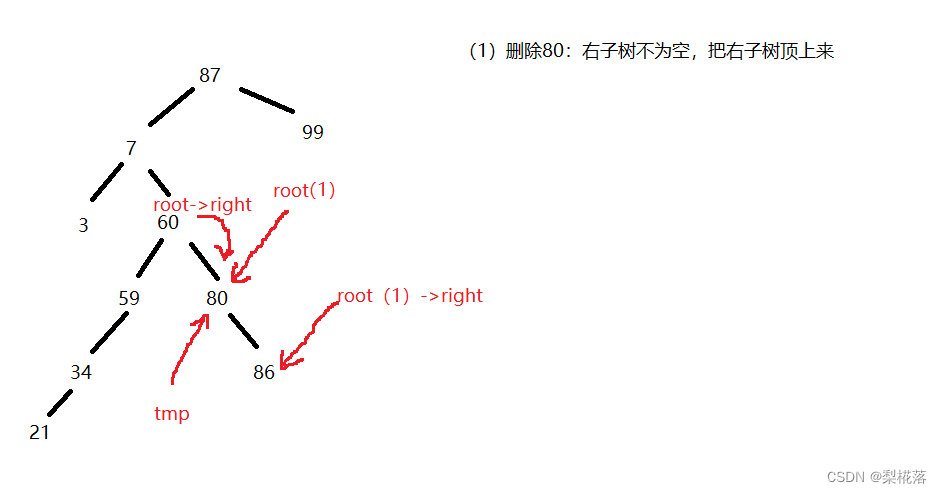
這時我們想讓root->right變為root(1)->right,而root(1)就是root->right的別名,因此我們直接讓root(1)=root(1)->right,然后去free(tmp),用代碼表示就是這樣:

同理,右子樹為空,把左子樹頂上去:

當左右子樹都不為空時,要么去左子樹中找最大的數據去替換刪除節點,要么去右子樹中找最小的數據去替換刪除節點。
而左子樹中的最大數據位于左子樹的最右深處節點,右子樹中的最小數據位于右子樹的最左深處節點。
什么是“替換”:把要刪除的根節點的值與左子樹最右節點的值交換,然后“刪除”掉左子樹最右節點;或者把要刪除的根節點的值與右子樹最左節點的值交換,然后“刪除”掉右子樹最左節點。

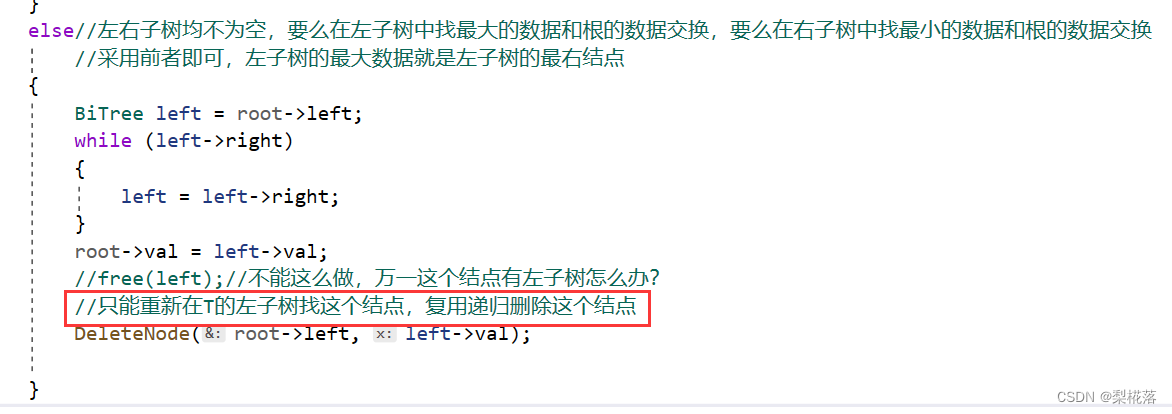
何為刪除?真的是直接free掉嗎?
 ?刪除59,那它的左子樹咋辦?直接free就坑了!
?刪除59,那它的左子樹咋辦?直接free就坑了!
復用函數去遞歸刪除59,讓59的左子樹頂上去:







)
))










