1 基本介紹
- OPTICS(Ordering points to identify the clustering structure)是一基于密度的聚類算法
- OPTICS算法是DBSCAN的改進版本
- 在DBCSAN算法中需要輸入兩個參數:???和 MinPts?,選擇不同的參數會導致最終聚類的結果千差萬別,因此DBCSAN對于輸入參數過于敏感
- ?機器學習筆記:DBSCAN_dbscan參數選取-CSDN博客
- OPTICS算法的提出就是為了幫助DBSCAN算法選擇合適的參數,降低輸入參數的敏感度
- OPTICS主要針對輸入參數?過敏感做的改進
- OPTICS和DBSCNA的輸入參數一樣( ? 和 MinPts? ),雖然OPTICS算法中也需要兩個輸入參數,但該算法對 ? 輸入不敏感(一般將 ? 固定為無窮大)【不太清楚為什么不直接不輸入ε呢?】
- 同時該算法中并不顯式的生成數據聚類,只是對數據集合中的對象進行排序,得到一個有序的對象列表
- 通過該有序列表,可以得到一個決策圖
- 通過決策圖可以不同 ? 參數的數據集中檢測簇集,
- 即:先通過固定的 MinPts? 和無窮大的 ? 得到有序列表,然后得到決策圖,通過決策圖可以知道當 ? 取特定值時(比如 ?=3 )數據的聚類情況。
- OPTICS算法是DBSCAN的改進版本
1.1 和DBSCAN相似的概念
- ε、minPts、核心點、邊緣點、噪點、密度直達(直接密度可達)、密度可達、密度相連 這些概念可見“機器學習筆記:DBSCAN_dbscan參數選取-CSDN博客
?1.2 OPTICS新的定義
1.2.1 核心距離
 換句話說,如果x不是核心點,那么cd(x)就沒有意義
換句話說,如果x不是核心點,那么cd(x)就沒有意義
1.2.2 可達距離

- 也是,如果x不是核心點,那么rd(y,x)沒有意義
- 如果y在x的ε領域內,那么rd(y,x)=cd(x);如果在x的ε領域外,那么就是d(y,x)
1.3 算法思想
假設數據集為,OPTICS算法的目標是輸出一個有序排列,以及每個元素的兩個屬性值:核心距離,可達距離。
1.3.1 OPTICS算法的數據結構

1.4 算法流程
- 輸入:數據集
,領域參數ε(一般等于∞),MinPts
- 創建兩個隊列,有序隊列O和結果隊列R
- 有序隊列用來存儲核心對象及其該核心對象的密度直達對象,并按可達距離升序排列
- 理解為待處理的數據
- 結果隊列用來存儲樣本點的輸出次序
- 已經處理完的數據
- 有序隊列用來存儲核心對象及其該核心對象的密度直達對象,并按可達距離升序排列
- 如果D中所有點都處理完畢或者不存在核心點,則算法結束。否則:
- 選擇一個未處理(即不在結果隊列R中)且為核心對象的樣本點 p
- 將 p 放入結果隊列R中,并從X中刪除 p
- 找到 X 中 p 的所有密度直達樣本點 x,計算 x 到 p 的可達距離
- 如果 x 不在有序隊列O 中,則將 x 以及可達距離放入 O 中
- 若 x 在O中,則如果 x 新的可達距離更小,則更新 x 的可達距離
- 最后對O中數據按可達距離從小到大重新排序。
- 如果有序隊列O為空,則回到步驟2,否則:
- 取出O 中第一個樣本點 y(即可達距離最小的樣本點),放入 R 中
- 從 D 和 O 中刪除 y
- 如果 y 不是核心對象,則重復步驟 3(即找 O 中剩余數據可達距離最小的樣本點)
- 如果 y 是核心對象,則
- 找到 y 在 D 中的所有密度直達樣本點
- 計算到 y 的可達距離
- 所有 y 的密度直達樣本點更新到 O 中
- 對O中數據按可達距離從小到大重新排序。
- 重復步驟2、3,直到算法結束。
- 最終可以得到一個有序的輸出結果,以及相應的可達距離。
1.5 舉例
樣本數據集為:D = {[1, 2], [2, 5], ?[8, 7], [3, 6], ?[8, 8], [7, 3], [4,5]}

假設eps = inf,min_samples=2,則數據集D在OPTICS算法上的執行步驟如下:
- 計算所有的核心對象和核心距離
- 因為 eps 為無窮大,則顯然每個樣本點都是核心對象
- 因為 min_samples=2,則每個核心對象的核心距離就是離自己最近樣本點到自己的距離(樣本點自身也是鄰域元素之一)
-
索引 0 1 2 3 4 5 6 元素 (1, 2) (2, 5) (8, 7) (3, 6) (8, 8) (7, 3) (4, 5) 核心距離 3.16 1.41 1.0 1.41 1.0 3.61 1.41
- 隨機在 D 中選擇一個核心對象
- 假設選擇?0 號元素,將 0 號元素放入 R 中,并從 D 中刪除
- 因為 eps = inf,則其他所有樣本點都是 0 號元素的密度直達對象
- 計算其他所有元素到 0 號元素的可達距離(計算所有元素到 0 號元素的歐氏距離)
- 按可達距離排序,添加到序列 O 中
- 此時D{1,2,3,4,5,6},R{0},O{1,6,3,5,2,4}
-
索引 0 1 2 3 4 5 6 核心對象 元素 (1, 2) (2, 5) (8, 7) (3, 6) (8, 8) (7, 3) (4, 5) 核心距離 3.16 1.41 1.0 1.41 1.0 3.61 1.41 第一次可達距離 -- 3.16 8.60 4.47 9.21 6.08 4.24 0
- 此時 O 中可達距離最小的元素是 1 號元素
- 取出 1 號元素放入 R ,并從 D 和 O?中刪除
- 因為 1 號元素是核心對象,找到?1?號元素在 D 中的所有密度直達對象(剩余的所有樣本點),并計算可達距離
- 同時更新 O
- 此時 D{2,3,4,5,6} R{0,1} O{3,6,5,2,4}
-
索引 0 1 2 3 4 5 6 核心對象 元素 (1, 2) (2, 5) (8, 7) (3, 6) (8, 8) (7, 3) (4, 5) 核心距離 3.16 1.41 1.0 1.41 1.0 3.61 1.41 第二次可達距離 -- -- 6.32 1.41 6.70 5.38 2.0 1
- 此時 O 中可達距離最小的元素是 3?號元素
- 取出 3?號元素放入 R ,并從 D 和 O 中刪除
- 因為 3?號元素是核心對象,找到 3?號元素在 D 中的所有密度直達對象(剩余的所有樣本點),并計算可達距離
- 同時更新 O
- 此時D{2,4,5,6} R{0,1,3} O{6,5,2,4}
-
索引 0 1 2 3 4 5 6 核心對象 元素 (1, 2) (2, 5) (8, 7) (3, 6) (8, 8) (7, 3) (4, 5) 核心距離 3.16 1.41 1.0 1.41 1.0 3.61 1.41 第三次可達距離 -- -- 5.09 -- 5.39 5.0 1.41 3
- 此時 O 中可達距離最小的元素是 6?號元素
- 取出 6?號元素放入 R ,并從 D 和 O 中刪除
- 因為 6?號元素是核心對象,找到 6?號元素在 D 中的所有密度直達對象(剩余的所有樣本點),并計算可達距離,同時更新 O
- 此時D{2,4,5},R{0,1,3,6},O(5,2,4}
-
索引 0 1 2 3 4 5 6 核心對象 元素 (1, 2) (2, 5) (8, 7) (3, 6) (8, 8) (7, 3) (4, 5) 核心距離 3.16 1.41 1.0 1.41 1.0 3.61 1.41 第四次可達距離 -- -- 4.47 -- 5.0 3.61 -- 6
- 此時 O 中可達距離最小的元素是 5 號元素
- 取出 5 號元素放入 R ,并從 D 和 O 中刪除
- 因為 5 號元素是核心對象,找到 5 號元素在 D 中的所有密度直達對象(剩余的所有樣本點),并計算可達距離,同時更新 O。
- 注意本次計算的4號元素到5號元素的可達距離是5.10,大于5.0,因此不更新4號元素的可達距離
- 此時D{2,4}R{0,1,3,6,5} O(2,4)
-
索引 0 1 2 3 4 5 6 核心對象 元素 (1, 2) (2, 5) (8, 7) (3, 6) (8, 8) (7, 3) (4, 5) 核心距離 3.16 1.41 1.0 1.41 1.0 3.61 1.41 第五次可達距離 -- -- 4.12 -- 5.0
(5.10)
-- -- 5
- 此時 O 中可達距離最小的元素是 2?號元素
- 取出 2?號元素放入 R ,并從 D 和 O 中刪除
- 因為 2?號元素是核心對象,找到 2?號元素在 D 中的所有密度直達對象,并計算可達距離,同時更新 O
-
索引 0 1 2 3 4 5 6 核心對象 元素 (1, 2) (2, 5) (8, 7) (3, 6) (8, 8) (7, 3) (4, 5) 核心距離 3.16 1.41 1.0 1.41 1.0 3.61 1.41 第六次可達距離 -- -- -- -- 1.0 -- -- 2
所以最后的R:(0,1,3,6,5,2,4)?,對應的可達距離為:{∞,3.16,1.41,1.41,3.61,4.12,1.0}
按照最終的輸出順序繪制可達距離圖
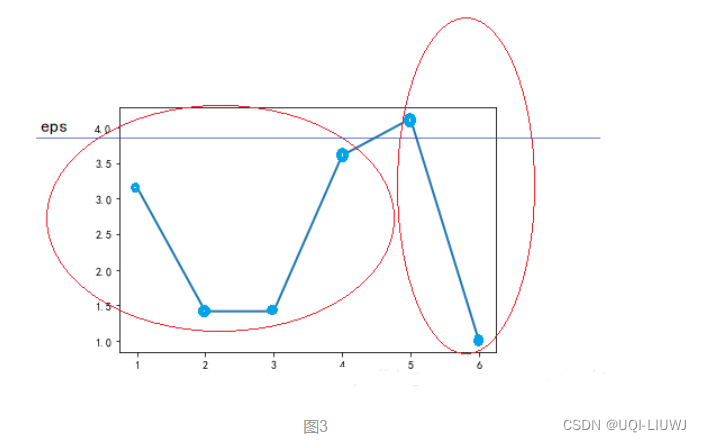
- 可以發現,可達距離呈現兩個波谷,也即表現為兩個簇,波谷越深,表示簇越緊密
- 只需要在兩個波谷之間取一個合適的 eps 分隔值(圖中藍色的直線),使用 DBSCAN 算法就會聚類為兩個簇。
- 即第一個簇的元素為:0、1、3、6、5;第二個簇的元素為:2、4。
1.4 和DBSCAN的異同
- OPTICS算法與DBSCAN算法有許多相似之處,可以被視為DBSCAN的一種泛化,它將eps要求從單一值放寬到值范圍
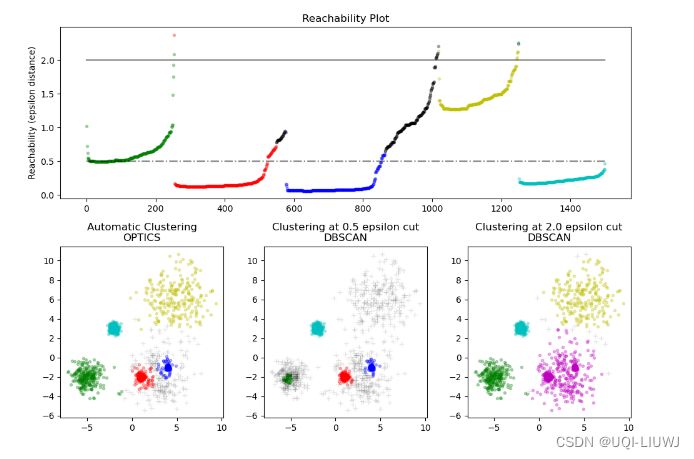
- DBSCAN和OPTICS之間的關鍵區別在于,OPTICS算法構建了一個可達性圖,為每個樣本分配了一個可達性距離和在集群排序屬性中的位置
- 這兩個屬性在模型擬合時被賦值,并用于確定集群成員資格
1.5 可達性距離
- OPTICS生成的可達性距離允許在單個數據集中提取可變密度的集群
- 結合可達性距離和數據集排序產生了一個可達性圖,其中點密度在Y軸上表示,點的排序使得附近的點相鄰
- 平行于x軸“切割”可達性圖產生了類似DBSCAN的結果:
- 所有在“切割”線以上的點被分類為噪聲
- 每當從左到右閱讀時出現間斷時,就標志著一個新的集群
- OPTICS的默認集群提取方法是查看圖中的陡峭斜坡以找到集群,可以使用xi參數定義什么算作陡峭斜坡
1.6 計算復雜度
- 空間索引樹用于避免計算完整的距離矩陣,并允許在大量樣本集上有效地使用內存
- 對于大型數據集,可以通過HDBSCAN獲得類似(但不完全相同)的結果。
- HDBSCAN實現是多線程的,并且比OPTICS具有更好的算法運行時間復雜性,但以較差的內存擴展為代價
2?sklearn.cluster.OPTICS
class sklearn.cluster.OPTICS(*, min_samples=5, max_eps=inf, metric='minkowski', p=2, metric_params=None, cluster_method='xi', eps=None, xi=0.05, predecessor_correction=True, min_cluster_size=None, algorithm='auto', leaf_size=30, memory=None, n_jobs=None)2.1 主要參數
| min_samples | int > 1 或介于0和1之間的浮點數,默認為5 點被視為核心點時,鄰域中的樣本數量 如果是浮點數,表示樣本數量的一部分 |
| max_eps | 兩個樣本被視為彼此鄰域的最大距離。 np.inf的默認值將識別所有規模的聚類; 降低max_eps將導致更短的運行時間 |
| metric | str或可調用,默認為'minkowski' 用于距離計算的度量。可以使用 來自scikit-learn:['cityblock', 'cosine', 'euclidean', 'l1', 'l2', 'manhattan'] 來自scipy.spatial.distance:['braycurtis', 'canberra', 'chebyshev', 'correlation', 'dice', 'hamming', 'jaccard', 'kulsinski', 'mahalanobis', 'minkowski', 'rogerstanimoto', 'russellrao', 'seuclidean', 'sokalmichener', 'sokalsneath', 'sqeuclidean', 'yule'] |
| p | 閔可夫斯基度量的參數 |
| xi | float在0和1之間,默認為0.05 確定可達性圖中構成聚類邊界的最小陡度。 例如,可達性圖中的向上點被定義為一個點與其后繼的比率最多為1-xi。 僅在cluster_method='xi'時使用 |
| min_cluster_size | int > 1 或介于0和1之間的浮點數,默認為None OPTICS聚類中的最小樣本數量,表示為絕對數量或樣本數量的一部分(至少為2)。如果為None,則使用min_samples的值。 僅在cluster_method='xi'時使用。 |
| algorithm | {'auto', 'ball_tree', 'kd_tree', 'brute'},默認為'auto' 用于計算最近鄰居的算法: 'ball_tree'將使用BallTree。 'kd_tree'將使用KDTree。 'brute'將使用蠻力搜索。 'auto'(默認)將嘗試根據傳遞給fit方法的值決定最合適的算法。 |
| leaf_size | 傳遞給BallTree或KDTree的葉子大小。這會影響構建和查詢的速度,以及存儲樹所需的內存。最佳值取決于問題的性質。 |
| cluster_method | str,默認為'xi' 使用計算的可達性和排序提取聚類的方法。可能的值是“xi”和“dbscan” |
2.2. 舉例
from sklearn.cluster import OPTICS
import numpy as npX = np.array([[1, 2], [1, 4], [1, 0],[10, 2], [10, 4], [10, 0]])op=OPTICS(min_samples=2).fit(X)op.labels_
#array([0, 0, 0, 1, 1, 1])op.ordering_
#array([0, 1, 2, 3, 4, 5])
#按聚類順序排列的樣本索引列表op.reachability_
#array([inf, 2., 2., 9., 2., 2.])
#按對象順序索引的每個樣本的可達距離op.core_distances_
#array([inf, 2., 2., 9., 2., 2.])
#每個樣本成為核心點的核心距離
#永遠不會成為核心的點的距離為無窮大。參考內容:機器學習筆記(十一)聚類算法OPTICS原理和實踐_optics聚類_大白兔黑又黑的博客-CSDN博客
(4)聚類算法之OPTICS算法 - 知乎 (zhihu.com)



)















