參考:https://www.hello-algo.com/chapter_tree/binary_tree/#711
1. 介紹
樹存儲不同于數組和鏈表的地方在于既可以保證數據檢索的速度,又可以保證數據插入刪除修改的速度,二者兼顧。
二叉樹是一種很重要的數據結構,是非線性的結構,
非常多其他數據結構都是基于二叉樹的基礎演變而來的。
如:一般二叉樹、完全二叉樹、滿二叉樹、線索二叉樹、哈夫曼樹、
二叉排序樹、平衡二叉樹、紅黑樹、B樹。
普通的二叉樹,很難構成現實的應用場景,但因其簡單,常用于學習研究,
平衡二叉樹則是實際應用比較多的。
常見于快速匹配、搜索等方面。
常用的樹有:AVL樹、紅黑樹、B+樹、Trie(字典)樹。
1、AVL樹: 最早的平衡二叉樹之一。應用相對其他數據結構比較少。windows對進程地址空間的管理用到了AVL樹。
2、紅黑樹: 平衡二叉樹,廣泛用在C++的STL中。如map和set都是用紅黑樹實現的。還有Linux文件管理。
3、B/B+樹: 用在磁盤文件組織 數據索引和數據庫索引。
4、Trie樹(字典樹): 用在統計和排序大量字符串,如自動機、M數據庫索引。
2 概念
2.1 二叉樹的每個節點最多只能有兩個子節點(左、右節點)
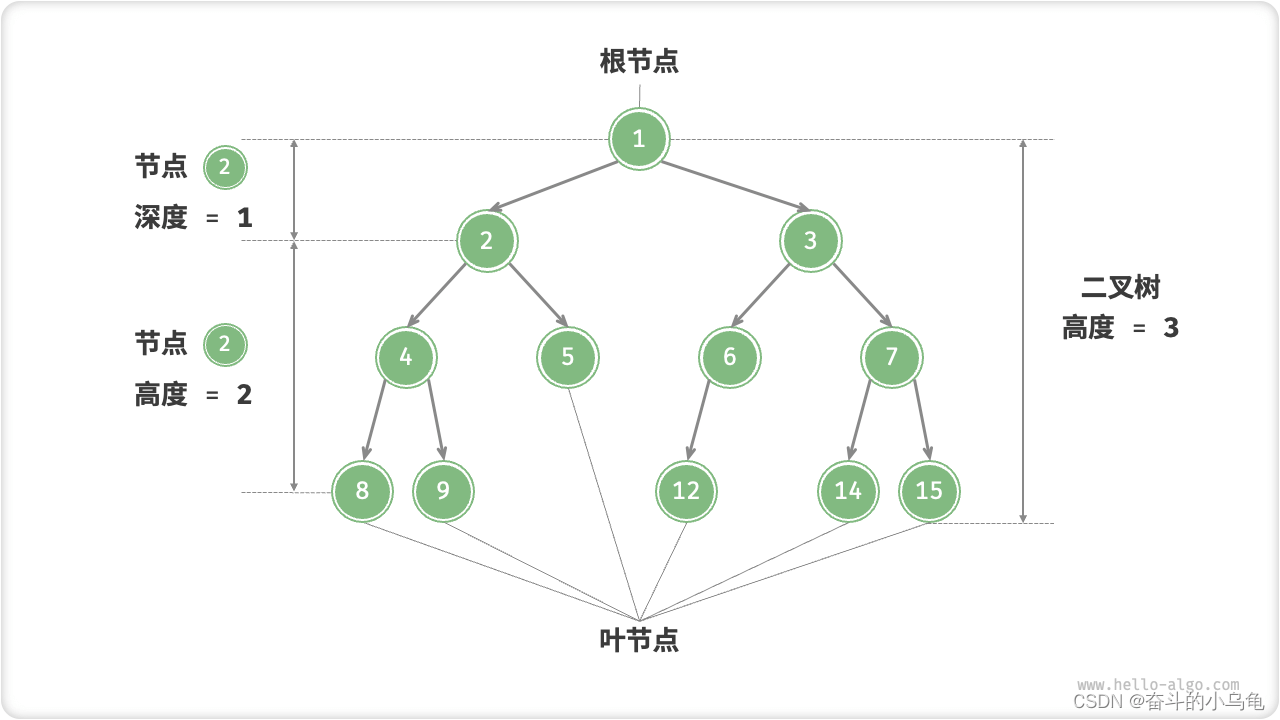
1. 「根節點 root node」:位于二叉樹頂層的節點,沒有父節點。
2. 「葉節點 leaf node」:沒有子節點的節點,其兩個指針均指向None
3. 「邊 edge」:連接兩個節點的線段,即節點引用(指針)。
4. 節點所在的「層 level」:從頂至底遞增,根節點所在層為 1 。
5. 節點的「度 degree」:節點的子節點的數量。在二叉樹中,度的取值范圍是 0、1、2 。
6. 二叉樹的「高度 height」:從根節點到最遠葉節點所經過的邊的數量。
7. 節點的「深度 depth」:從根節點到該節點所經過的邊的數量。
8. 節點的「高度 height」:從距離該節點最遠的葉節點到該節點所經過的邊的數量。
2.2 完全二叉樹
若設二叉樹的高度為h,除第 h 層外,其它各層 (1~h-1) 的結點數都達到最大個數,第h層有葉子結點,并且葉子結點都是從左到右依次排布,這就是完全二叉樹。
特征:
葉子結點只可能在最下面的兩層上出現,對任意結點,若其右分支下的子孫最大層次為L,則其左分支下的子孫的最大層次必為L或L+1
圖示:
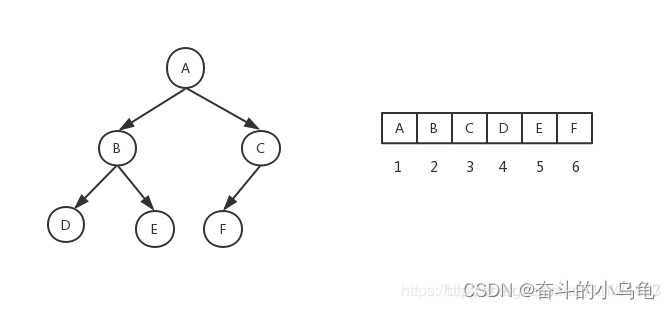
特點:
(1)若i為奇數且i>1,那么tree[i]的左兄弟為tree[i-1];(2)若i為偶數且i<n,那么tree[i]的右兄弟為tree[i+1];(3)若i>1,tree[i]的雙親為tree[i div 2];(4)若2*i<=n,那么tree[i]的左孩子為tree[2*i];若2*i+1<=n,那么tree[i]的右孩子為tree[2*i+1];(5)若i>n/2,那么tree[i]為葉子結點(對應于(3));(6)若i<(n-1)/2,那么tree必有兩個孩子(對應于(4));(7)滿二叉樹一定是完全二叉樹,完全二叉樹不一定是滿二叉樹;(8)完全二叉樹第i層至多有2^(i-1)個節點,共i層的完全二叉樹最多有2^i-1個節點。


)














)
