深度學習模型訓練計算量的估算

在當今的機器學習領域，深度學習模型的性能和先進性往往與其在更多計算資源上進行的訓練有關。為了確保不同深度學習模型之間的準確比較，估算和報告訓練過程中的計算資源使用情況變得至關重要。

本文將探討深度學習模型訓練計算量的估算方法，并介紹了該領域的一些前沿。

計算資源的使用通常以訓練模型的最終版本所需的浮點運算次數（FLOP）來衡量。

我們將重點介紹兩種估算方法，以大家更好地理解和比較不同深度學習模型的訓練計算量，這兩種方法用于估算深度學習模型的訓練計算量：

• 一種基于網絡架構和批處理數量
• 一種基于硬件的最大配置和模型訓練時間

方法1：基于網絡架構和批處理數量計算算術運算次數

這種方法通過分析模型的架構和訓練數據量來估算計算量。我們將探討如何通過這種信息來估算模型訓練的計算資源需求，以及其在實際研究中的應用。

大致公式如下：

$$計算量=2\times connections\times 3\times trainingexample\times epochs$$

connections：指的是神經網絡中的連接數，即神經元之間的直接相互連接。在神經網絡中，神經元之間的連接表示它們之間的信息傳遞和相互作用。

舉個例子，如果你有一個具有 N 個輸入神經元和 M 個輸出神經元的全連接層（fully connected layer），那么它將有 NM 個連接。這意味著每個輸入神經元都與每個輸出神經元相連接，形成了 NM 個連接。

training example：指的是用于訓練機器學習模型的數據集中的樣本數量
epochs：是指在訓練深度學習模型時的迭代次數

計算資源的使用通常是以模型的前向傳播（inference）或反向傳播（backpropagation）所需的浮點運算次數（FLOP）來衡量。這是在單次迭代（一個batch）中的計算，而不是迭代的總和，在深度學習框架中，每個批次計算完成后，框架通常會自動釋放相應的計算資源，包括中間結果的內存。

為什么不可以層層計算，釋放資源，進入下一層呢？

在神經網絡的訓練中，每一層的計算都依賴于前一層的輸出，因此不能在每一層的計算中釋放資源并進入下一層。神經網絡的計算通常是流水線式的，每一層的輸出是下一層的輸入。如果在每一層都等待上一層計算完成并釋放資源，會導致整個計算過程變得非常慢。

下面我們可以將上面的公式翻譯轉換一下，可以用如下公式來解釋：

$$training\_compute=(ops\_per\_forward\_pass+ops\_per\_backward\_pass)?n\_passes$$

其中：

• ops_per_forward_pass：表示的是前向傳播中的計算數
• ops_per_backward_pass：是反向傳播中的計算數
• n_passes：等于模型迭代次數和訓練樣本數的乘積：

$$n\_passes=n\_epochs?n\_examples$$

如果不知道自己一個迭代的訓練樣本數，有時可以計算為每個迭代的批次數乘以每個批次的大小

$$n\_examples=n\_batches?batch\_size$$

ops_per_backward_pass與ops_per_forward_pass的比率相對穩定，因此可以將二者整合為

$$fp\_to\_bp\_ratio=\frac{ops\_per\_backward\_pass}{ops\_per\_forward\_pass}$$。

得到以下公式：

$$training\_compute=ops\_per\_forward\_pass?(1+fp\_to\_bp\_ratio)?n\_passes$$

通常估計fp_to_bp_ratio的值為2:1 。最終的公式為：
$$training\_compute=ops\_per\_forward\_pass?3?n\_epochs?n\_examples$$

為什么反向傳遞操作與前向傳遞操作的比率2:1

計算反向傳遞需要為每一層計算與權重相關的梯度和每個神經元關于要回傳的層輸入的誤差梯度。這些操作中的每一個需要的計算量大致等于該層前向傳遞中的操作量。因此，fp_to_bp_ratio約為2:1。

為什么權重更新參數計算可以忽略不計

在深度學習訓練中，權重更新所需的參數計算量相對于前向傳播和反向傳播來說，通常可以被認為是可以忽略不計的。這主要有以下幾個原因：

1. 批量更新： 在深度學習中，通常使用批量梯度下降或小批量梯度下降等優化算法進行權重更新。這意味著權重更新是基于整個訓練數據集或小批次的梯度。相比于前向傳播和反向傳播，其中需要對每個訓練樣本進行計算，權重更新的計算是在更大的數據集上進行的，因此其計算量相對較小。
2. 累積梯度： 在實際應用中，通常會累積多個批次的梯度來更新參數。這樣做有助于降低梯度的方差，提高梯度估計的穩定性。由于梯度的累積，單個批次中的權重更新計算相對于整體訓練過程來說是較小的一部分。
3. 參數共享： 在卷積神經網絡（CNN）等架構中，存在參數共享的情況。在這種情況下，多個神經元共享同一組權重，從而減少了參數的數量。由于參數共享，權重的梯度計算是相對較小的。

前向傳遞計算和常見層的參數數量

下面是整理了一個常見神經網絡層的表格，估算了它們的參數數量以及每層前向傳遞所需的浮點運算次數。

前文已經知道了，在許多層中，前向傳遞中的FLOP數量大致等于參數數量的兩倍，然而，有許多例外情況，例如CNN由于參數共享而具有更少的參數，而詞嵌入則不進行任何操作。

全連接層（Fully connected layer）

參數

浮點數計算量

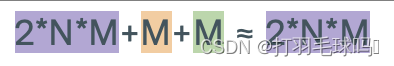
CNN

從形狀為 $H\times W\times C$ 的張量中使用形狀為 $K\times K\times C$的 D 個濾波器，應用步幅為 S 和填充為 P 的卷積神經網絡（CNN）。

參數

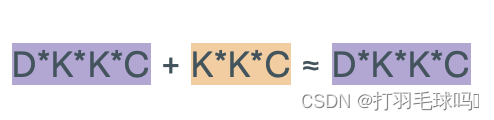
浮點數計算量

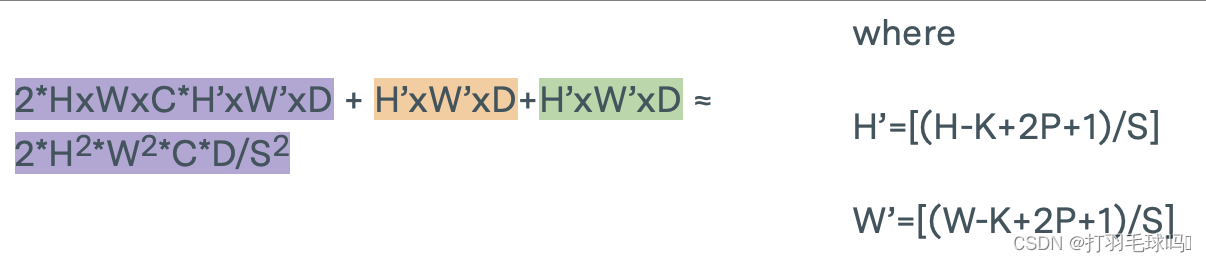
轉置CNN

從形狀為 $H\times W\times C$ 的張量中使用形狀為 $K\times K\times C$的 D 個濾波器，應用步幅為 S、填充為 P 的轉置卷積神經網絡（Transpose CNN）。

參數

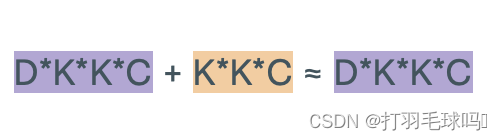
浮點數計算量

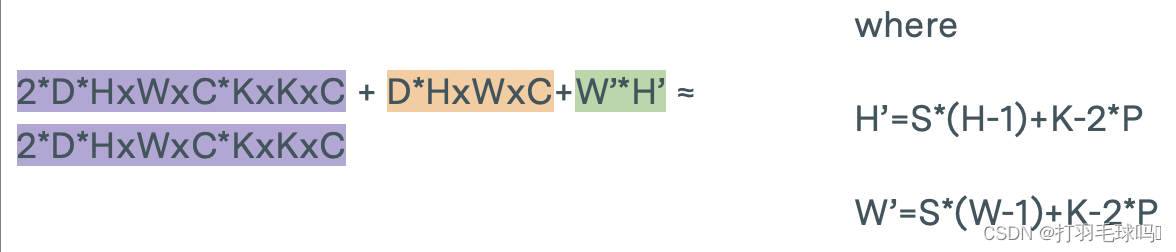
RNN

帶有偏置向量的循環神經網絡（RNN），其輸入大小為 N，輸出大小為 M。

參數

浮點數計算量

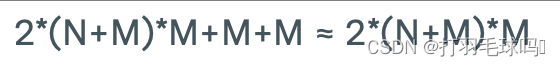
GRU

帶有偏置向量的全門控門循環單元（Fully Gated GRU），其輸入大小為 N，輸出大小為 M。

參數

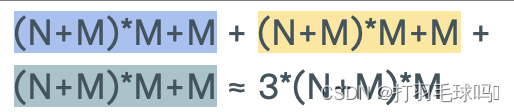
浮點數計算量

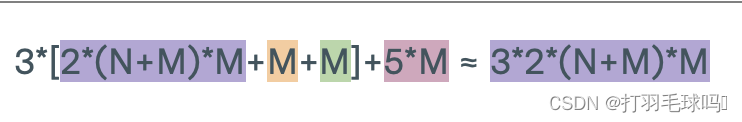
LSTM

帶有偏置向量的長短時記憶網絡（LSTM），其輸入大小為 N，輸出大小為 M。

參數

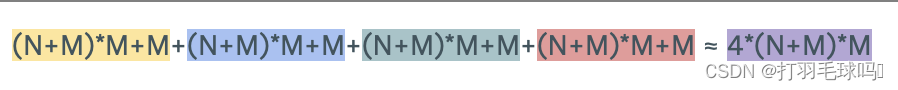
浮點數計算量

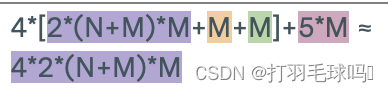
Self-Attention

具有序列長度 L、輸入大小為 W、鍵大小為 D 和輸出大小為 N 的自注意力層（Self-Attention Layer）。

參數

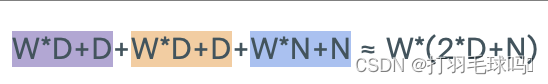
浮點數計算量

Multi-Headed Attention

具有序列長度 L、輸入大小為 W、鍵大小為 D、每個注意力頭輸出大小為 N、最終輸出大小為 M 以及 H 個注意力頭的多頭注意力層（Multi-Headed Attention Layer）。

參數

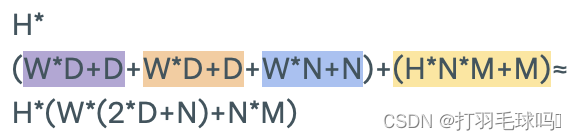
浮點數計算量

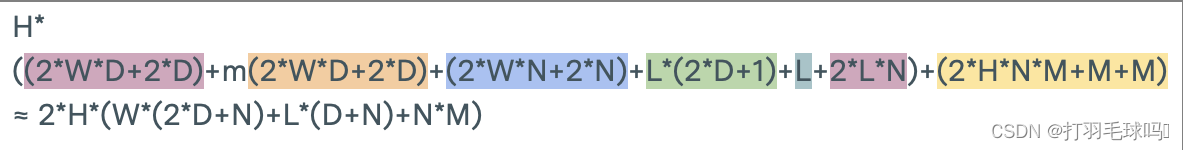
示例：CNN-LSTM-FCN模型

例如，假設我們有一個CNN-LSTM-FCN架構，具體如下：

• 輸入是形狀為 [400x400x5] 的圖像序列。
• 每個輸入序列的平均長度為20張圖像。
• CNN 具有16個形狀為 5x5x5 的濾波器，應用步幅為2，填充為2。
• LSTM 是一個多對一層，具有256個輸出單元和偏置向量。
• 全連接層有10個輸出單元。
• 訓練過程經過10個時期，每個時期包含100個大小為128的序列批次。
  
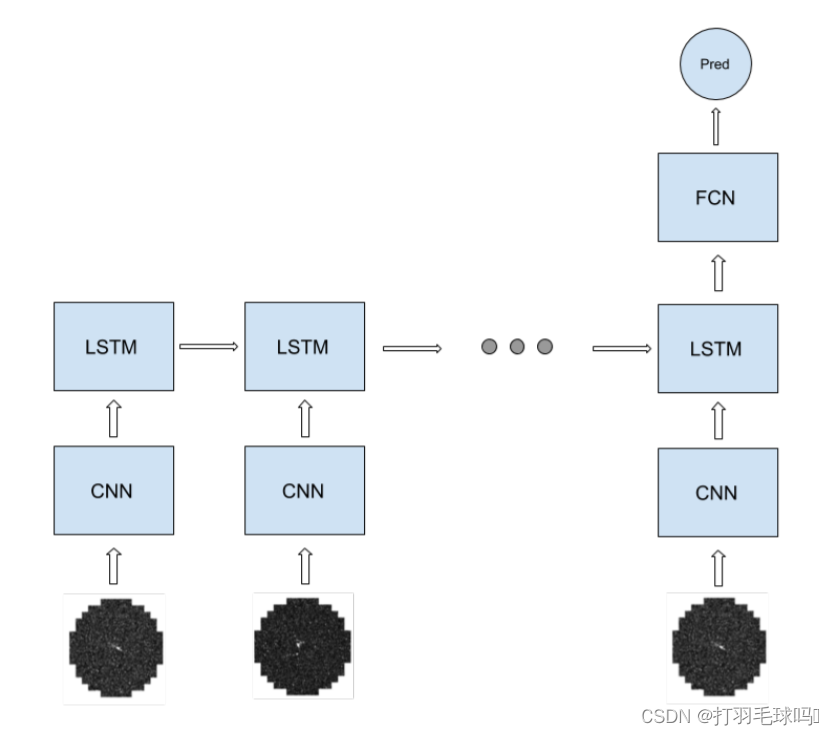
  當我們考慮一個CNN-LSTM-FCN模型時，循環部分包括CNN和LSTM，而FC則是網絡的非循環部分。

首先，CNN接受一個形狀為$400?400?5$的輸入圖像序列。該CNN有16個5x5x5的濾波器，應用步幅為2，填充為2。它產生一個輸出，寬度和高度為$H’=W’=[(W?K+2P)/S]+1=[(400?5+2?2+1)/2]=200$，通道數為16。整個CNN的前向傳遞需要約$1.024\times 10^{12}$ 次浮點運算（FLOP）。

在將輸入饋送到LSTM之前，CNN的輸出被重新排列成一個$200?200?16$的輸入。然后，LSTM中每個序列標記的操作數量約為$1.31\times 10^9$FLOP。最后，全連接層（FC）有10個輸出單元，它需要5120 FLOP。

整個網絡的非循環部分相對較小，我們可以將總操作數近似為：

$$training\_compute\approx ops\_per\_forward\_pass\_recurrent\times 3\times n\_epochs\times n\_batches\times batch\_size\times avg\_tokens\_per\_sequence\approx 1.024\times 10^{12}FLOP\times 3\times 10\times 100\times 128\times 20=7.86432\times 10^{18}FLOP$$

方法2：基于硬件設置和訓練時間計算運算次數

另一種估算方法涉及考慮所使用的硬件和訓練時間。我們將研究如何利用這些硬件方面的信息來估算計算資源的使用情況，并探討硬件選擇如何影響深度學習模型的性能和效率。

傳統的基于硬件設置和訓練時間計算運算次數是用使用GPU天數做為標準。

GPU使用天數：描述了單個GPU用于訓練的累積天數。如果訓練持續了5天，總共使用了4個GPU，那等于20個GPU天數。

傳統的用GPU天數來估算計算資源的方法存在一些問題。首先，它只關注訓練所使用的時間，而忽略了訓練過程中所使用的計算硬件的性能。在十年內，GPU的性能顯著提升，因此相同的GPU天數在不同時期所完成的實際計算工作量可能存在巨大差異。

此外，該方法沒有考慮到不同硬件設置之間的差異。同樣的GPU天數在不同的硬件配置下可能導致不同數量的浮點運算。因此，為了更準確地估算計算資源的使用情況，我們需要考慮硬件性能和配置的影響。

因此我們需要用GPU時間結合硬件配置估算FLOP，具體步驟如下

1.從論文/參考文獻中提取信息：

在深入研究模型相關論文時，我們需要從中提取以下關鍵信息：

1. GPU天數的數量：論文中應該包含關于訓練模型所用GPU的天數，這反映了模型在訓練期間的計算資源使用情況。
2. 所使用的計算系統/GPU：論文應該明確說明在訓練期間使用的計算系統或GPU型號，這對于了解硬件規格和性能至關重要。
3. 訓練運行期間使用的浮點數數字表示：論文應提供關于訓練運行期間所采用的數字表示的信息，如FP32、FP16、BF16、INT8等。這直接關系到模型在計算過程中使用的精度。

2.閱讀硬件規格

通過閱讀硬件規格表，我們可以獲取以下信息：

1. GPU/系統的型號：通過查閱制造商的規格表，我們可以確定所使用的GPU或計算系統的具體型號。此信息對于計算性能的準確評估至關重要。
2. GPU的峰值性能：規格表通常包含GPU的峰值性能，以FLOP/s（每秒浮點運算次數）為單位。這是評估硬件計算能力的關鍵指標。

以下是NVIDIA A100的示例：

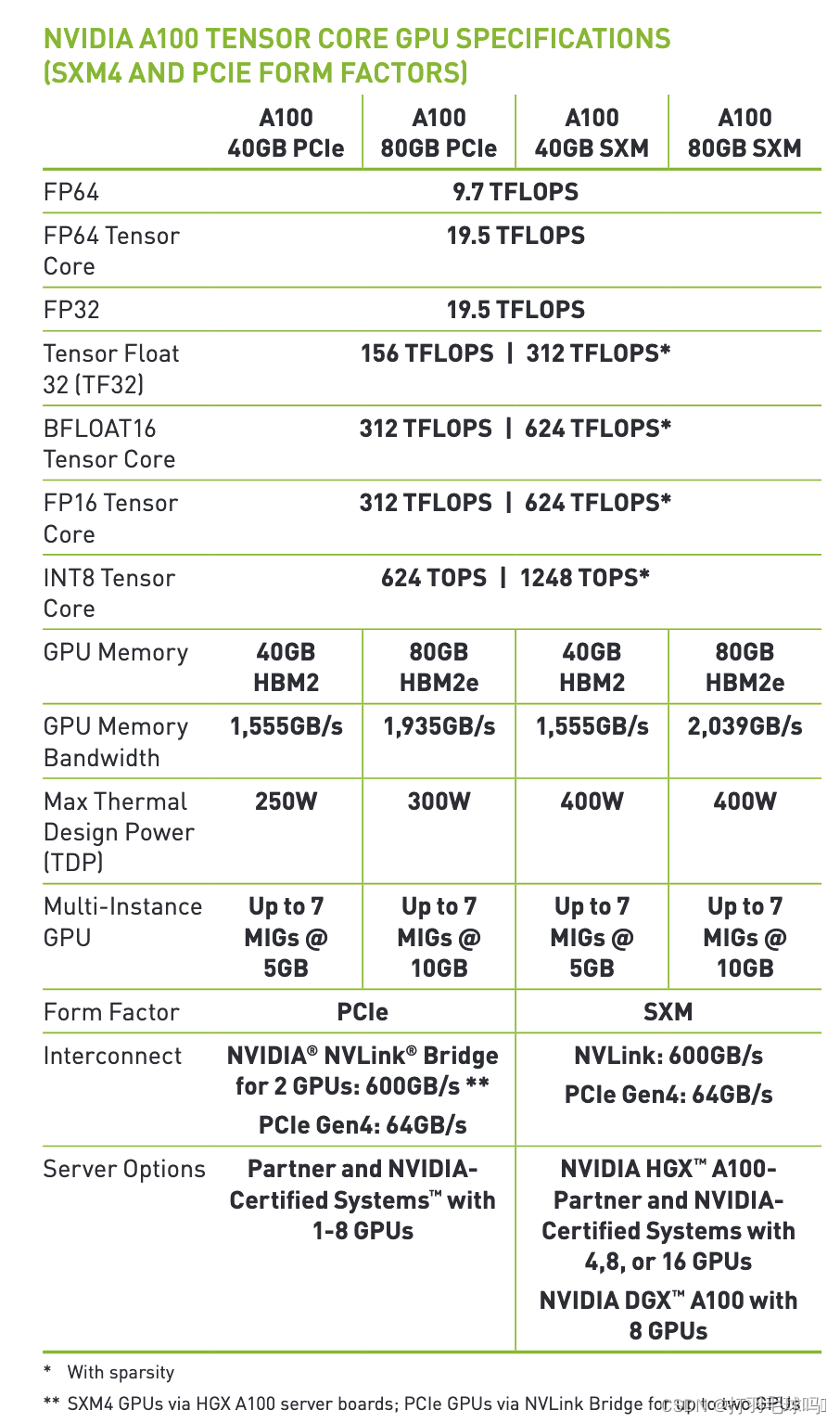
如果您找不到使用過的硬件或上述硬件的規格，建議參考下面鏈接里的表格，估計給定年份的平均計算能力。您還可以在下面的框中找到每年峰值表現的圖表。

ML Hardware Data sheet

3.進行估算

綜合上述信息，我們可以進行如下估算：

估算GPU的總FLOP：

步驟 1：計算單個GPU的峰值性能

從硬件規格表中獲取GPU的峰值性能，表示為FLOP/s。例如，若峰值性能為 $X$ FLOP/s。

步驟 2：計算總的GPU FLOP

通過將單個GPU的峰值性能乘以GPU使用的天數，我們得到總的GPU FLOP。假設GPU使用天數為 Y 天，那么總的GPU FLOP 為 $X\times Y$。

精度的考慮：

步驟 1：確定訓練使用的數字表示

從論文中獲取模型在訓練期間使用的數字表示，如FP32、FP16等。

步驟 2：確定每個數字表示的FLOP數

根據不同數字表示的標準，確定每個數字表示所需的FLOP數。例如，FP32可能需要 $A$ FLOP，FP16可能需要 $B$FLOP。

步驟 3：計算總的FLOP數

將每個數字表示所需的FLOP數與模型中相應數字表示的使用情況相乘，得到總的FLOP數。假設使用了FP32和FP16，總FLOP數為
$A\times 數量1+B\times 數量2$。

考慮硬件特性：

步驟 1：檢查是否使用了張量核心

查閱硬件規格表或相關文獻，確定是否啟用了NVIDIA的張量核心。如果啟用，我們可以考慮這一特性對性能的影響。

步驟 2：了解張量核心的使用情況

若啟用了張量核心，了解它在模型訓練中的具體使用情況。這可能涉及到特殊的參數設置或架構要求。

步驟 3：調整總的GPU FLOP

如果使用了張量核心，可以根據其使用情況調整總的GPU FLOP。這可能需要根據具體情況進行一些額外的計算和估算。

通過這些詳細的步驟，我們可以更準確地估算模型在訓練期間的計算資源使用情況，考慮到不同精度和硬件特性的影響。