五、動態規劃

基本概念

階段（Stage）：將所給問題的過程，按時間或空間特征分解成若干相互聯系的階段，以便按次序去求解每階段的解，常用字母 $k$ 表示。

狀態（State）：各階段開始時的客觀條件叫做狀態。描述各階段狀態的變量稱為狀態變量，常用 $s_k$ 表示第 $k$ 階段的狀態變量，狀態變量 $s_k$ 的取值集合稱為狀態集合，用 $S_k$ 表示。狀態變量應具有無后效性：某階段狀態給定后，這個階段以后過程的發展不受這段以前各狀態的影響。

決策和策略（Decision and Policy）：各階段狀態確定后，就可以作不同的決定，從而確定下一階段的狀態，這種決定稱為決策。表示決策的變量稱為決策變量，常用 $u_k(s_k)$ 表示，允許的決策集合常用 $D_k(s_k)$ 表示。各階段決策確定后，整個問題的決策序列就構成一個策略。

狀態轉移方程：如果給定了第 $k$ 階段的狀態 $s_k$ ，本階段決策為 $u_k(s_k)$ ，則第 $k+1$ 階段的狀態 $s_{k+1}$ 也就完全確定，它們的關系就稱為狀態轉移方程。

指標函數：用于衡量所選定策略優劣的數量指標稱為指標函數。直接指標函數表示某階段的決策產生的效益，常用 $d_k(u_k)$ 表示。最優指標函數表示從第 $k$ 階段狀態為 $s_k$ 采用最優策略時，后部過程的最優收益值，常用 $f_k(s_k)$ 表示。

五要素

動態規劃模型五要素：

1. 將問題按時空特征恰當地劃分為若干個階段。
2. 正確地規定狀態變量 $s_k$ ，使得它既能描述過程的演變，又具有無后效性。
3. 正確地規定決策變量 $u_k$ 以及每階段的允許決策集合 $D_k(s_k)$ .
4. 正確寫出狀態轉移方程 $s_{k+1}=g_k(s_k,u_k)$ 。
5. 正確地定義各階段的直接指標函數 $d_k(s_k,u_k)$ 和后部子過程的最優指標函數 $f_k(s_k)$ ，并寫出基本方程（以 $\max$ 和相加求收益為例）： { f k ( s k ) = max ? { d k ( s k , u k ) + f k + 1 ( s k + 1 ) } , k = n , n ? 1 , ? , 1 f n + 1 ( s n + 1 ) = 0 , 邊界條件 \begin{cases} f_k(s_k)=\max\{d_k(s_k,u_k)+f_{k+1}(s_{k+1})\} &,k=n,n-1,\cdots,1 \\ f_{n+1}(s_{n+1})=0&,邊界條件\end{cases} {fk?(sk?)=max{dk?(sk?,uk?)+fk+1?(sk+1?)}fn+1?(sn+1?)=0?,k=n,n?1,?,1,邊界條件?

生產存儲問題

做題時，我們可也按照動態規劃模型五要素進行建模，以生產與儲存問題為例。

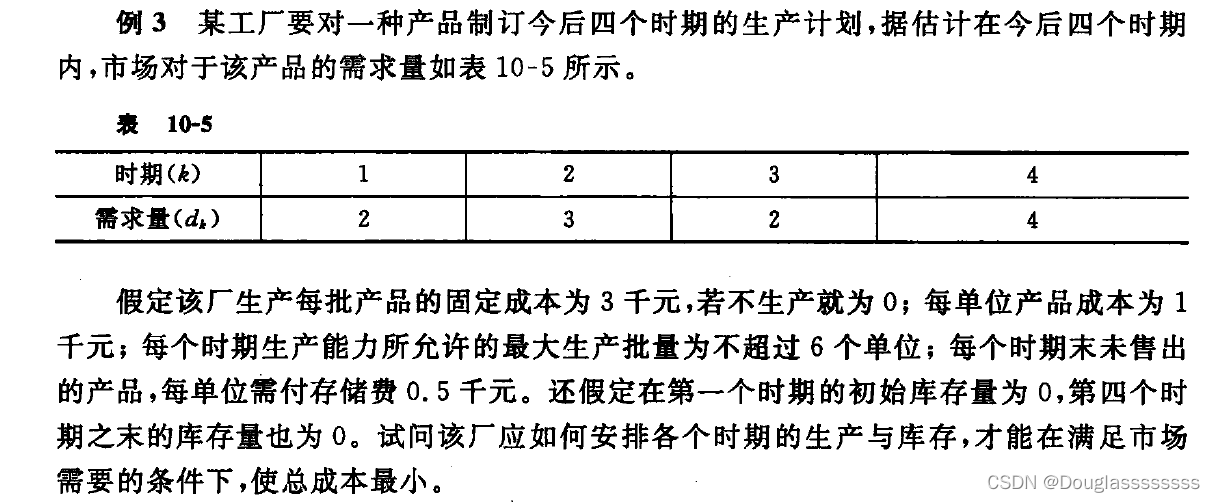
解： 將問題劃分為 $4$ 個階段（$k=1,2,3,4$），每個階段表示一個時期；狀態變量 $s_k$ 表示第 $k$ 階段開始時的庫存量；決策變量 $x_k$ 表示第 $k$ 階段的產品生產量，$d_k$ 表示第 $k$ 階段的產品需求量，則狀態轉移方程為：$$s_{k+1}=s_k+x_k?d_k$$ 直接指標函數 $g_k(x_k)$ 表示第 $k$ 階段決策為 $x_k$ 時的成本，包括生產成本 $c_k(x_k)$ 和存儲成本 $m_k(x_k)$ 。其中，$$c_k(x_k)=?\begin{array}{ll}0& ,x_k=0\\ 3+x_k& ,x_k=1,2,?,6\\ \infty & ,x_k>6\end{array}$$ $m_k(x_k)=0.5(s_k+x_k?d_k)$ 。最優指標函數 $f_k(s_k)$ 表示第 $k$ 階段狀態為 $s_k$ 采用最優策略時，后部過程的最小成本，則遞推基本方程為： f k ( s k ) = { min ? { c k ( x k ) + m k ( x k ) + f k + 1 ( s k + 1 ) } , k = 4 , 3 , 2 , 1 f 5 ( s 5 ) = 0 f_k(s_k)=\begin{cases} \min\{c_k(x_k)+m_k(x_k)+f_{k+1}(s_{k+1})\},k=4,3,2,1\\ f_5(s_5)=0\end{cases} fk?(sk?)={min{ck?(xk?)+mk?(xk?)+fk+1?(sk+1?)},k=4,3,2,1f5?(s5?)=0? 隨后便是每個階段的求解了，最關鍵的就是確定 $s_k$ 和 $x_k$ 的取值范圍，需要瞻前顧后，考慮每階段的生產能力以及最后階段的庫存要求。

設備更新問題

對于設備更新問題，教材上用了別的符號，讓人難以和之前的聯系起來，但其實它也可以用我們常見的符號表達的。用一個實際題目來說明。

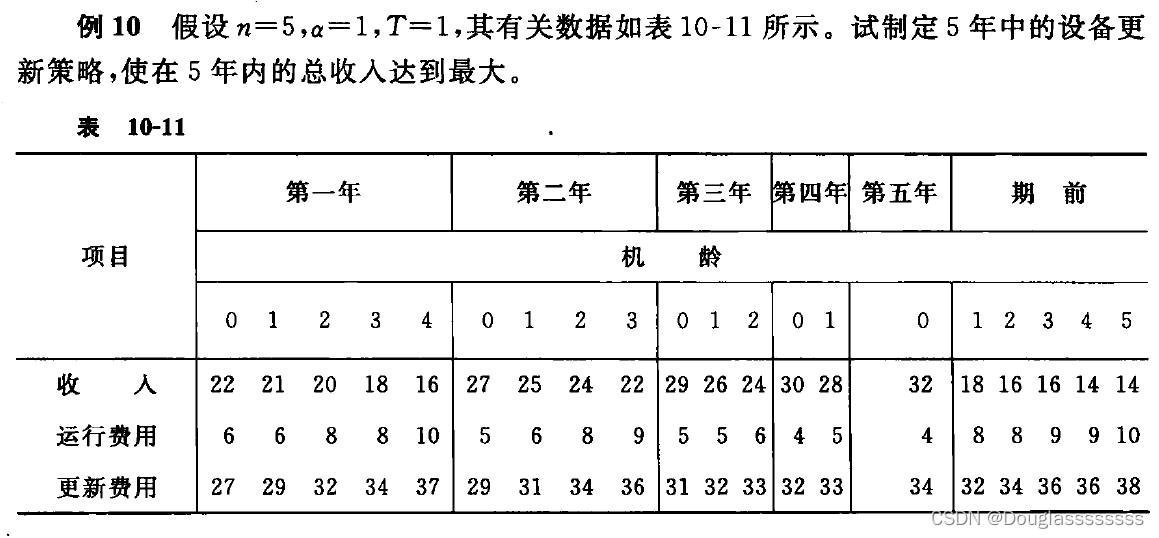
解： 將問題分為 5 個階段（$k=1,2,3,4,5$），每個階段代表一年。狀態變量 $s_k$ 表示第 $k$ 階段初機器的役齡，決策變量 $x_k$ 表示第 $k$ 階段時保留（K）還是更新（R）。則狀態轉移方程為：$$s_{k+1}=\{\begin{array}{ll}{s}_k+1& ,x_k=K\\ 1& ,x_k=R\end{array}$$ 直接指標函數 $g_k(x_k)$ 表示第 $k$ 階段做出決策 $x_k$ 的收入，$I_k(s_k)$ 表示第 $k$ 階段役齡為 $s_k$ 的機器帶來的收入，$O_k(s_k)$ 表示第 $k$ 階段役齡為 $s_k$ 的機器的運行費用，$C_k(s_k)$ 表示第 $k$ 階段役齡為 $s_k$ 的機器更新費用，則有 $$g_k(x_k)=\{\begin{array}{ll}{I}_k(s_k)?O_k(s_k)& ,x_k=K\\ I_k(0)?O_k(0)?C_k(s_k)& ,x_k=R\end{array}$$ 最優指標函數 $f_k(s_k)$ 表示第 $k$ 階段役齡為 $s_k$ 的機器采用最優策略時，后部過程的最大收入，可寫出遞推基本方程為： f k ( s k ) = { max ? { g k ( x k ) + f k + 1 ( s k + 1 ) } , k = 5 , 4 , 3 , 2 , 1 f 6 ( s 6 ) = 0 f_k(s_k)=\begin{cases} \max\{g_k(x_k)+f_{k+1}(s_{k+1})\},k=5,4,3,2,1\\ f_6(s_6)=0\end{cases} fk?(sk?)={max{gk?(xk?)+fk+1?(sk+1?)},k=5,4,3,2,1f6?(s6?)=0? 剩下就是根據表中的數據代入遞推方程了。

靜態規劃問題

動態規劃方法還可以用來求解一些靜態規劃問題，如整數規劃和非線性規劃問題等。一般將約束條件的右端資源量作為狀態變量，決策變量為原規劃問題的決策變量，直接指標函數為目標函數對應的部分。

有時候最后一個階段的直接指標函數較為復雜，可以換一換次序，簡化計算。

---