紅黑樹:
一種接近平衡的二叉樹,平衡程度低于搜索二叉樹。
特點:
1.根節點為黑
2.黑色結點的子結點可以是紅色結點或黑色結點。
3.紅色結點的子結點只能是黑色結點。
4.每個結點到其所有葉子結點的路徑的黑色結點個數相同。
5.指向空的結點,指向空的那一側視為指向黑色結點(指向nullptr的黑色結點,用于明確路徑)
6.由于上述規則,使得紅黑樹任意結點的左右子樹高度差不超過二倍(最小是全黑,最大是紅黑相交,又由于黑色結點個數需要一致,因此高度不會超過二倍)。
模擬實現紅黑樹:
1.紅黑樹的插入:
// 注意:為了簡單起見,本次實現紅黑樹不存儲重復性元素bool Insert(const T& data){if (_pHead == nullptr){Node* cur = new Node(data);_pHead = cur;_pHead->_color = black;return true;}//有根節點的時候Node* cur = new Node(data);Node* news = _pHead;Node* parent = nullptr;//查找插入位置while (news != nullptr){if (news->_data < data){ parent = news;news = news->_pRight;}else if (news->_data > data){ parent = news;news = news->_pLeft;}else{return false;}}//確定插入位置是parent的左還是右if (parent->_data < data){parent->_pRight = cur;cur->_pParent = parent;}else{parent->_pLeft = cur;cur->_pParent = parent;}//開始向上判斷//若父節點為黑則可以正常插入,無任何影響//父節點為紅才進入,若父節點為空則cur指向根結點同樣退出while (parent&&parent->_color==red){ Node* grandparent = parent->_pParent;//parent為紅則一定有父節點if(grandparent->_color==black){//得到uncleNode* uncle = nullptr;if (parent->_data < grandparent->_data){uncle = grandparent->_pRight;}else{uncle = grandparent->_pLeft;}//判斷uncle情況if (uncle && uncle->_color == red){ //UNCLE存在且是紅parent->_color = uncle->_color = black;grandparent->_color = red;cur = grandparent;parent = cur->_pParent;}else{//uncle為黑或者uncle為空if (cur == parent->_pLeft&& parent == grandparent->_pLeft){//右旋RotateR(grandparent);//更新顏色parent->_color = black;grandparent->_color = red;}else if (cur == parent->_pRight&& parent == grandparent->_pRight){//左旋RotateL(grandparent);//更新顏色parent->_color = black;grandparent->_color = red;}//更新后當前子樹的根節點為黑,無需向上繼續判斷,因此parent->_color可以直接使得退出循環else if(cur == parent->_pRight&& parent == grandparent->_pLeft){//先左旋parent再右旋grandparentRotateL(parent);RotateR(grandparent);cur->_color = black;grandparent->_color = red;break;}else{RotateR(parent);RotateL(grandparent);cur->_color = black;grandparent->_color = red;break;}}}else{ //此時grandparent和parent顏色均是紅,報錯cout << parent->_data<<"出現連續紅結點" << endl;assert(false);}}_pHead->_color = black;}// 左單旋void RotateL(Node* pParent){Node* parent = pParent;Node* pr = parent->_pRight;Node* prl = pr->_pLeft;//記錄父節點Node* pp = parent->_pParent;//更新指針parent->_pRight = prl;if (prl)//判斷prl是否存在prl->_pParent = parent;pr->_pLeft = parent;parent->_pParent = pr;if (pp == nullptr){//若parent是根節點_pHead = pr;pr->_pParent = nullptr;}else{ //父節點連接if (pp->_data < parent->_data){pp->_pRight = pr;pr->_pParent = pp;}else{pp->_pLeft = pr;pr->_pParent = pp;}}}// 右單旋void RotateR(Node* pParent){Node* parent = pParent;Node* pl = parent->_pLeft;Node* plr = pl->_pRight;//記錄父節點Node* pp = parent->_pParent;//更新指針parent->_pLeft = plr;if (plr)//判斷prl是否存在plr->_pParent = parent;pl->_pRight = parent;parent->_pParent = pl;if (pp == nullptr){//若parent是根節點_pHead = pl;pl->_pParent = nullptr;}else{ //父節點連接if (pp->_data < parent->_data){pp->_pRight = pl;pl->_pParent = pp;}else{pp->_pLeft = pl;pl->_pParent = pp;}}}插入一個結點,初始時插入結點為紅(若為黑則會導致其祖先結點每條路徑黑色結點的個數改變,修改十分麻煩)。若此時父節點為黑,則無需進行任何其余操作。
若父節點為紅,此時會出現連續紅色結點的情況,不符合紅黑樹的定義,因此需要修改。
修改主要分以下幾種情況:
1.
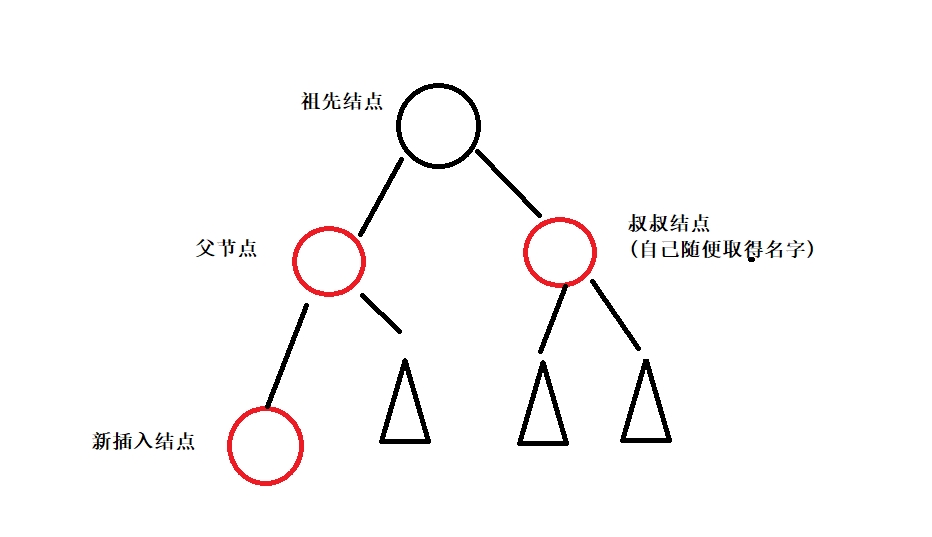
此時叔叔結點存在且為紅色。
修改方式是將父節點和叔叔結點改成黑色,祖先結點改成紅色,然后將祖先結點視為新插入結點繼續向上判斷。此時父節點和叔叔結點改成黑色,不會受其子節點顏色的影響,且對于祖先結點的父節點,每條路徑的黑色結點的個數沒有變化,因此仍符合紅黑樹。
2.
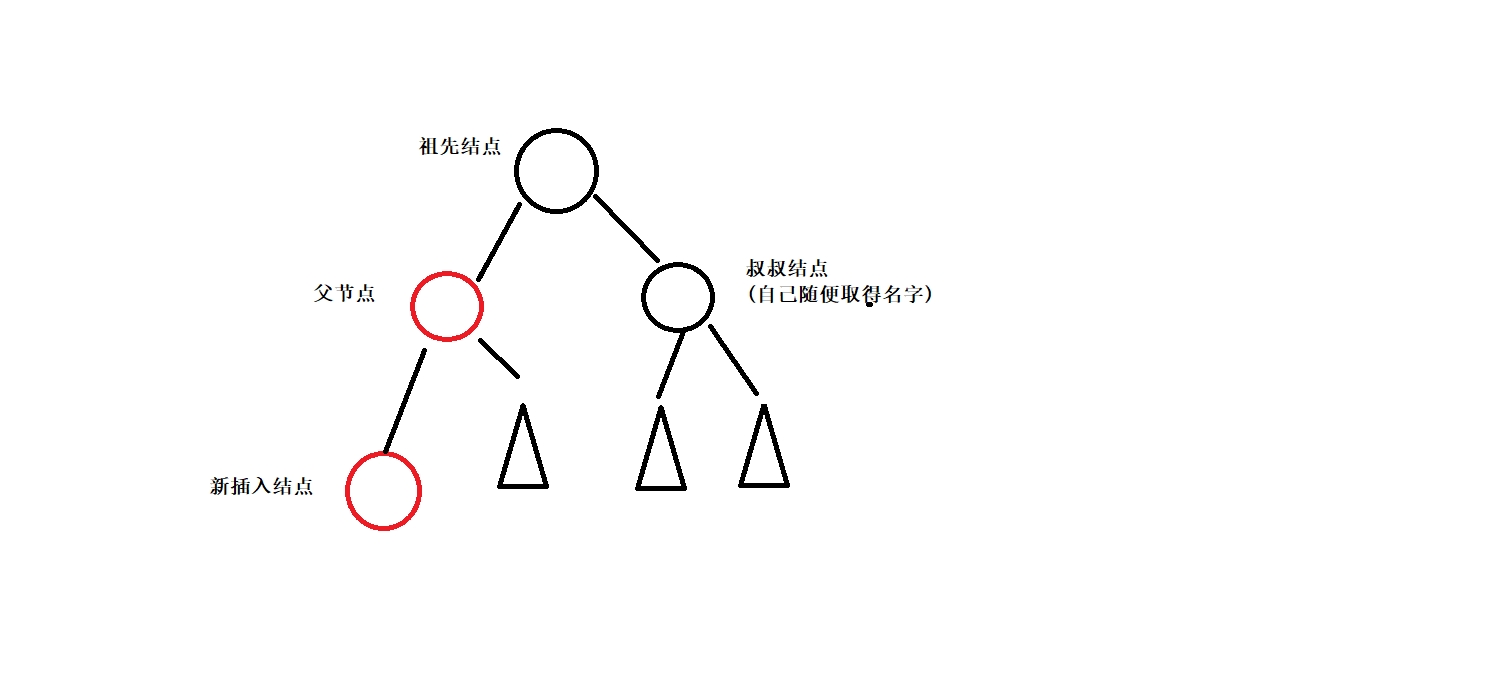
此時叔叔結點為黑色結點或者不存在(不存在的情況,根據紅黑樹規則指向空的結點,指向空的那一側視為指向黑色結點,因此也可以看做叔叔結點為黑色結點)。此時需要進行旋轉來修改這棵子樹。若祖先結點和父節點以及新插入結點都在同一側(比如父節點是祖先結點左子樹,新插入結點是父節點的左子樹),則只需要對祖先結點進行一次旋轉,旋轉完成后將父節點改成黑色,祖先結點改成紅色即可。若不在同一側,則需要先對父節點進行一次旋轉,再對祖先結點進行一次旋轉,旋轉完成后新插入結點的顏色為黑,祖先結點顏色為紅。
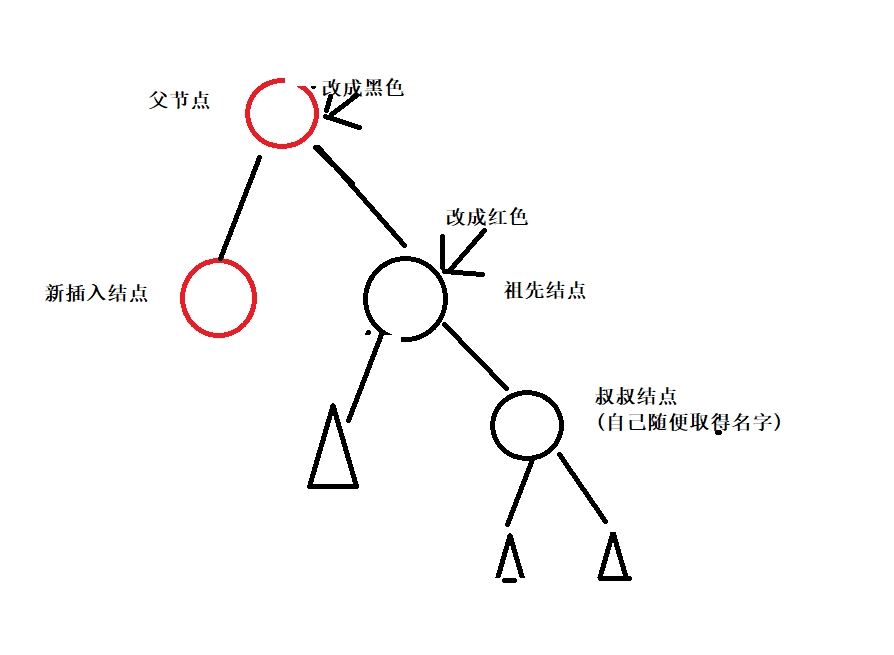
在同一側的旋轉一次。
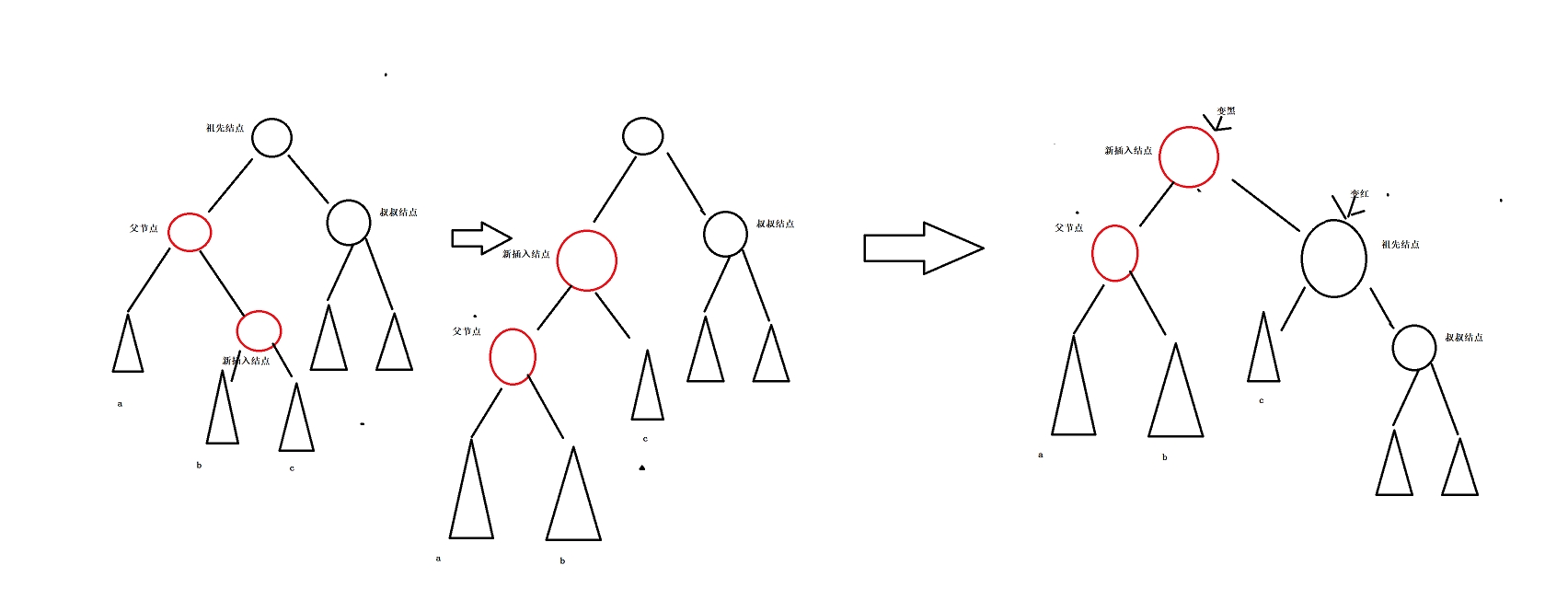
不在同一側,旋轉兩次。

)

)


)
】文件和異常詳解:使用、讀取、寫入、追加、保存用戶的信息,以及優雅的處理異常)


)







)
