前言?

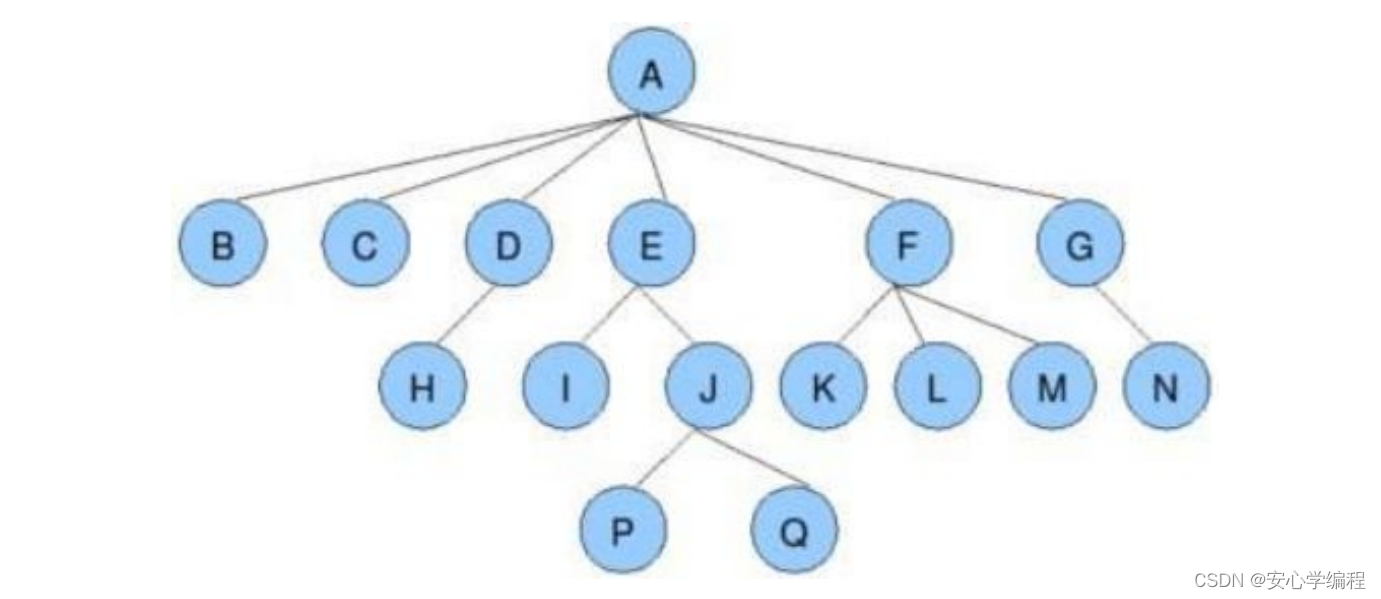
如上圖，A中的孩子的個數是不固定的。我們無法精確的每個不同的根結點有多少個孩子。所以并不能精確知道需要定義多少個孩子節點。

struct TreeNode
{int val;struct TreeNode* child1;struct TreeNode* child2;struct TreeNode* child3;//...//這樣顯然是不能的
};

樹的表示

指針數組表示法

? ?

#define N 6
//假設數的度為6
struct TreeNode
{int val;struct TreeNode* childArr[N];//指針數組-這些指針指向孩子數組
};

但是很顯然這個指針數組定義樹的存儲時有一個前提：那就是這個樹的度是確定好的。

并且一個樹的度是所有結點中最大度的結點的度，但是并不是每一個結點的度均為樹的度，而是小于或者等于。那么這樣就會出現一種情況，好多節點的指針就會浪費。

順序表表示法

那么解決這種情況，可以利用我們以前學習的順序表，需要幾個就插入幾個。

struct TreeNode
{int val;SeqList childSL;//順序表存儲孩子
};

左孩子右兄弟表示法（重點）

樹結構相對線性表就比較復雜了，要存儲表示起來就比較麻煩了，既然保存值域，也要保存結點和結點之間的關系，實際中樹有很多種表示方式如：雙親表示法，孩子表示法、孩子雙親表示法以及孩子兄弟表示法 等。我們這里就簡單的了解其中最常用的孩子兄弟表示法。?

//左孩子右兄弟
struct TreeNode
{int val;struct TreeNode* leftchild;struct TreeNode* rightbrother;
};

舉一個簡單的例子就是，假如我要生小孩，我想要生三個小孩，但是我覺得生三個小孩很麻煩，帶三個小孩很累啊，那我就可以先生老大，等老大有能力照顧弟弟妹妹的時候，我再生老二，同理再過幾年讓老二帶老三，那這樣我就可以輕松一點啦~

那么這里的“左孩子右兄弟”的原理也是類似的，我們可以看一下下面的圖例：

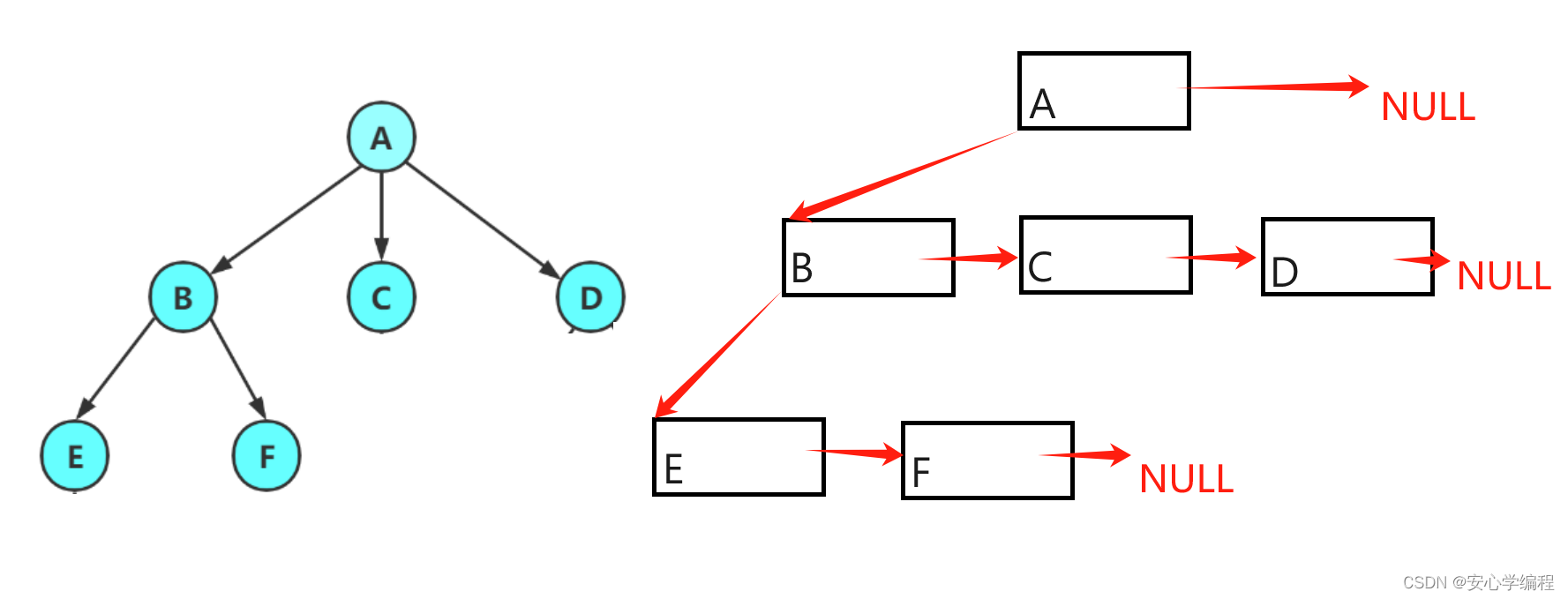
樹的實際應用

那么在實際情況中，我們什么時候會遇到樹呢？

在學習Linux操作系統中，我們可以知道Linux的文件系統的目錄樹，文件系統就是一個樹形結構。當前目錄下可以有很多個文件夾或者文件，那么文件夾就有可能是葉子，也有可能
會分下去，每個下面可以有任意多個孩子，那就是一個樹形結構。

• 我們平時敲在Linux中敲的ls，其實底層就是鏈式結構的遍歷，通過找到父節點，然后找到第一個孩子，然后第一個孩子再去用兄弟指針找到把所有的兄弟都找出來。
• 所以在Linux中，我們所學習的指令本質也就是一串代碼。每一個命令底層就是一個程序。目錄相關的文件相關的都是程序。
• 但是在Windows操作系統中，其實就是一個森林，假如在電腦上插入一個U盤的話，那么就是一個森林。例如C盤、D盤、E盤等也就是一個森林。