01背包問題

題目鏈接：

題目頁面

求解思路：

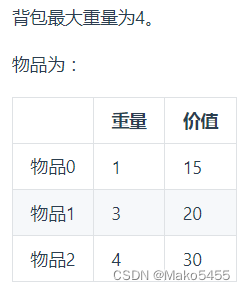
1. 確定dp數組及其下標含義：dp[i][j] 表示從下標為 [0] 到 [i] 的物品里任意選取，放進容量為j的背包，此時的價值總和最大值
2. 確定遞推公式：
   不放物品i，總和為dp[i-1][j]；
   放物品i，總和為 dp[i - 1][j - weight[i]] + value[i]；
   因此遞推公式為 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
3. dp數組的初始化：注意第一行，dp[0][j]，即i為0，存放編號0的物品的時候。當 j < weight[0]的時候，dp[0][j] 應該是 0，因為背包容量比編號0的物品重量還小；當j >= weight[0]時，dp[0][j] 應該是value[0]，因為背包容量放足夠放編號0物品
4. 確定遍歷順序：有兩個遍歷的維度，分別為物品與背包重量，本題中先遍歷哪個都可以
5. 舉例推導dp數組：如圖所示

代碼：

#include <bits/stdc++.h>
using namespace std;int n, bagweight;
void solve(){vector<int> weight(n, 0); // 每件物品所占空間vector<int> value(n, 0); // 每件物品的價值for (int i = 0; i < n; i++){cin >> weight[i];}for (int j = 0; j < n; j++){cin >> value[j];}// 先將dp數組全部初始化為0vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));// 當只有1件物品的時候（第一行）的初始化for (int j = weight[0]; j <= bagweight; j++){dp[0][j] = value[0];}// 開始遍歷for (int i = 1; i < weight.size(); i++){ // 遍歷物品for (int j = 0; j <= bagweight; j++){ // 遍歷背包if (j < weight[i]) // 放不下的情況dp[i][j] = dp[i-1][j];else dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i]);}}cout << dp[weight.size()-1][bagweight] << endl;
}int main(){cin >> n >> bagweight;solve();return 0;
}

01背包問題（滾動數組）

題目鏈接：

卡碼網KamaCoder

求解思路：

對于背包問題其實狀態都是可以壓縮的。

在使用二維數組的時候，遞推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

其實可以發現如果把dp[i - 1]那一層拷貝到dp[i]上，表達式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);

與其把dp[i - 1]這一層拷貝到dp[i]上，不如只用一個一維數組了，只用dp[j]（一維數組，也可以理解是一個滾動數組）。

這就是滾動數組的由來，需要滿足的條件是上一層可以重復利用，直接拷貝到當前層。

動規五部曲

1. 確定dp數組的意義：dp[j] 表示容量為j的背包，所背的物品最大價值為 dp[j]
2. 確定遞推公式：根據上文可知，dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
3. dp數組的初始化：因為背包容量為0所背的物品的最大價值就是0，所以dp[0] = 0；dp[j] 在計算的時候會加上自身來判斷更大的值，且所有物品價值大于0，為了讓值不被初始值覆蓋，其他下標也都初始化成0
4. 遍歷順序：注意必須倒序遍歷，并且先遍歷物品再遍歷背包。
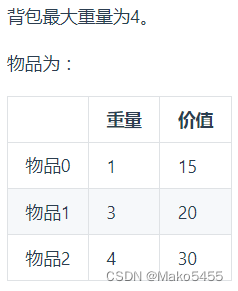
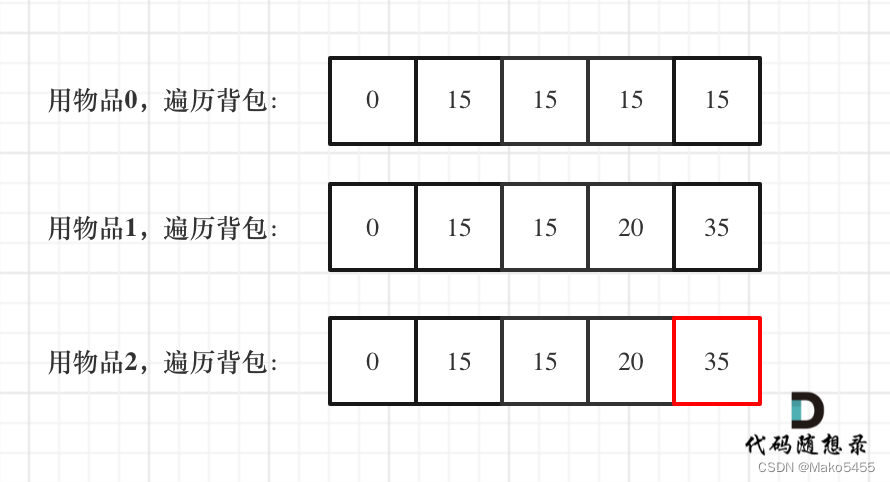
5. 舉例推導dp數組：如圖所示

代碼：

#include <iostream>
#include <vector>
using namespace std;int main(){int M, N;cin >> M >> N;vector<int> costs(M);vector<int> values(M);for (int i = 0; i < M; i++)cin >> costs[i];for (int i = 0; i < M; i++)cin >> values[i];vector<int> dp(N+1, 0);for (int i = 0; i < M; i++){for (int j = N; j >= costs[i]; j--){dp[j] = max(dp[j], dp[j-costs[i]] + values[i]);}}cout << dp[N] << endl;return 0;
}

416. 分割等和子集

題目鏈接：

力扣（LeetCode）官網 - 全球極客摯愛的技術成長平臺

求解思路：

分割成兩個等和子集，等于找出和為一半的子集，等于一個容量為數組和一半的背包可以被數組里的數裝滿。

注意事項

• 背包的體積為sum / 2
• 背包要放入的商品（集合里的元素）重量為 元素的數值，價值也為元素的數值
• 背包如果正好裝滿，說明找到了總和為 sum / 2 的子集。
• 背包中每一個元素是不可重復放入。

動規五部曲

1. 確定dp數組及其下標含義：dp[j] 表示背包總容量為j，放進物品后，背包的最大重量為dp[j]
2. 確定遞推公式：因為物品i的重量和價值都是nums[i]，所以 dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
3. dp數組的初始化：dp[0] = 0，其他下標也為0（因為價值都是正數）
4. 遍歷順序：先物品，再背包，并且背包要倒序遍歷（參考前面滾動數組）
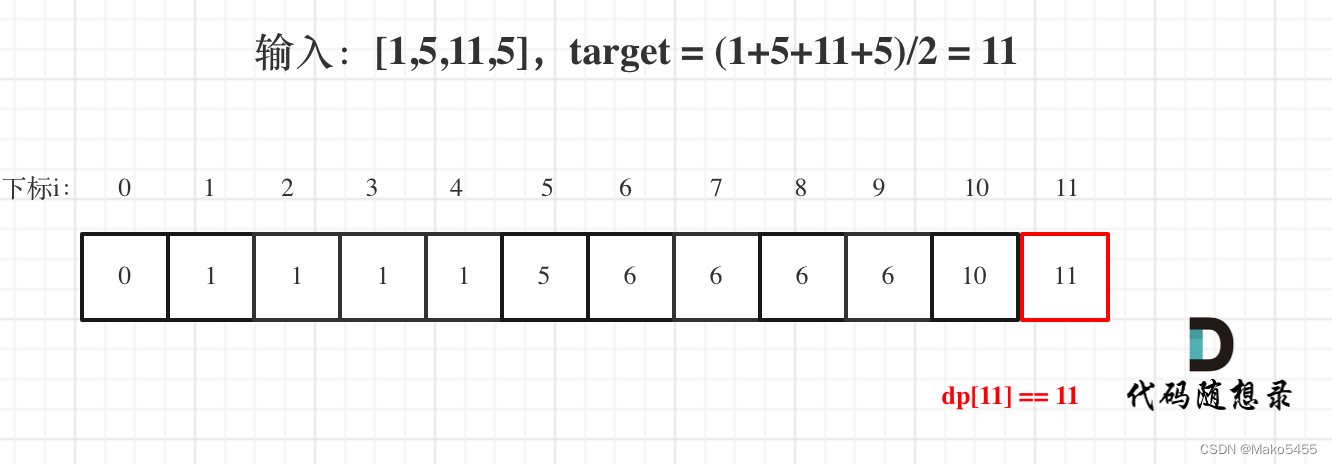
5. 舉例推導dp數組：以[1,5,11,5]為例，如圖

代碼：

class Solution {
public:bool canPartition(vector<int>& nums) {// 求和int sum = 0;for (int i : nums) sum+= i;// 和為奇數不可能有解if (sum % 2 == 1) return false;// 01背包int target = sum / 2;vector<int> dp(target+1, 0);for (int i = 0; i < nums.size(); i++){for (int j = target; j >= nums[i]; j--){dp[j] = max(dp[j], dp[j-nums[i]] + nums[i]);if (dp[j] == target) return true;}}return false;}
};