算法的復雜度分析
什么是算法復雜度？
不同的算法，其實效率是不一樣的
讓我舉一個案例來比較兩種不同的算法在查找數組中給定元素的時間復雜度
[1,2,3,4,5,6,7,...9999,n]
順序查找
這種方法從頭到尾遍歷整個數組，依次比較每個元素和給定元素的值。
如果找到想等元素，則返回下標，如果遍歷整個數組都找不到就返回-1。
function sequenSearch(array:number[],target:number) {let result = -1for (let i = 0;i<array.length;i++) {array[i] === target ? result = i : undefined}return result
}
最長時間復雜度：n
平均的時間復雜度: n / 2
該算法時間復雜度是O(n)
二分查找
這種算法假設數組是有序的，每次選擇數組中間的元素與給定元素進行比較。
如果找到想等元素，則返回下，如果給定的元素比中間元素小，則在數組左半部分繼續查找；如果給定的元素比中間元素大，則在數組右半部分繼續查找。
這樣每次查找都會將查找的范圍減半，知道找到想等的元素或者查找范圍為空。
function binarySearch(array: number[], target: number) {let left = 0;let right = array.length - 1;while (left <= right) {let mid = Math.floor((left + right) / 2);const midTarget = array[mid];if (midTarget === target) {return mid;} else if (midTarget < target) {left = mid + 1;} else {right = mid - 1;}}return -1;
}
最長時間復雜度：log(n,2)
平均的時間復雜度: log(n,2) / 2
該算法時間復雜度是O(log n)
大O表示法（Big O notation）
大O表示法(Big O notation)英文翻譯為大O符號（維基百科翻譯)，中文通常翻譯為大O表示法（標記法)。
- 這個記號則是在德國數論學家愛德蒙·蘭道的著作中才推廣的，因此它有時又稱為蘭道符號(Landau symbols)。
- 代表“order of …”.……階)的大O，最初是一個大寫希臘字母“O”(omicron)，現今用的是大寫拉丁字母“O”。
時間復雜度
分析算法時間效率舉例
-
舉個例子，解決一個規模為n的問題所花費的時間（或者所需步驟的數目)可以表示為:
T(n)=4n2-2n＋2 -
當
n增大時，n2項開始占據主導地位，其他各項可以被忽略; -
舉例說明:當
n=500 -
4n2項是2n項的1000倍大，因此在大多數場合下，省略后者對表達式的值的影響將是可以忽略不計的。
進一步看，如果我們與任一其他級的表達式比較， n2的系數也是無關緊要的。
這樣，針對第一個例子T(n) = 4n2- 2n＋2，大O符號就記下剩余的部分，寫作:
T(n) ∈ o(n2)
或
T(n)= o(n2)
我們就說該例子算法具有**n2**階（平方階）的時間復雜度，表示為**O(n2)**
常用函數階
介紹
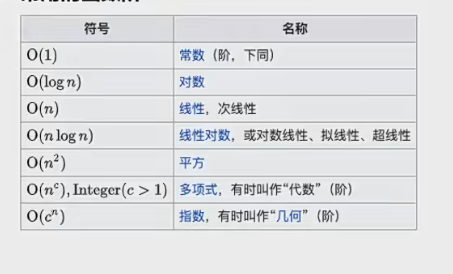
案例
圖表
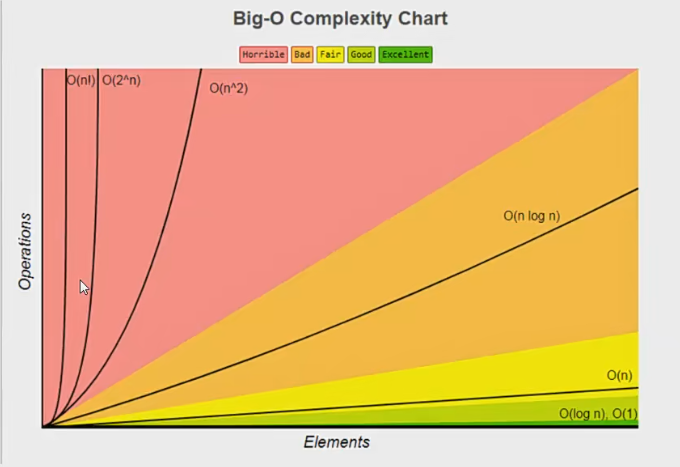
空間復雜度
空間復雜度指的是程序運行過程中所需要的額外存儲空間。
空間復雜度也可以用大O表示法來表示;
空間復雜度的計算方法與時間復雜度類似，通常需要分析程序中需要額外分配的內存空間，如數組、變量、對象、遞歸調用等。
分析算法空間效率舉例
舉個栗子:
對于一個簡單的遞歸算法來說，每次調用都會在內存中分配新的棧幀，這些棧幀占用了額外的空間。
-
因此，該算法的空間復雜度是o(n)，其中n是遞歸深度。
而對于迭代算法來說，在每次迭代中不需要分配額外的空間，因此其空間復雜度為o(1)。
當空間復雜度很大時，可能會導致內存不足，程序崩潰。
在平時進行算法優化時，我們通常會進行如下的考慮: -
使用盡量少的空間(優化空間復雜度);
-
使用盡量少的時間（優化時間復雜度);
-
特定情況下:使用空間換時間或使用時間換空間;
