最近在看時間序列的文章，回顧下經典
論文地址
項目地址

---

---

3.2、季節性

企業時間序列通常由于它們所代表的人類行為而具有多期季節性。例如，5天的工作周可以在時間序列上產生每周重復的效應，而假期安排和學校放假可以產生每年重復的效應。為了擬合和預測這些效應，我們必須指定季節性模型，這些模型是關于 t 的周期函數。

我們依靠傅立葉級數提供周期效應的靈活模型（Harvey & Shephard 1993）。讓 P 表示我們期望時間序列具有的常規周期（例如，對于年度數據，P = 365.25；對于每周數據，當我們將時間變量按天計算時，P = 7）。我們可以用傅立葉級數來近似任意平滑的季節效應

$s(t)={\sum }_{n=1}^N(a_{n}cos(\frac{2\pi nt}{P})+b_{n}sin(\frac{2\pi nt}{P}))$

標準傅立葉級數。擬合季節性需要估計2N個參數$\beta =[a_1,b_1,...,a_N,b_N{]}^{\text{T}}$。這是通過為歷史和未來數據中的每個 t 值構建一個季節性向量矩陣來完成的，例如，對于每年的季節性和 N = 10。

$X(t)=\left[\begin{array}{c}cos(\frac{2\pi (1)t}{356.25}),...,sin(\frac{2\pi (10)t}{356.25})\end{array}\right]$ (5)

季節性成分是

$s(t)=X(t)\beta$ (6)

在我們的生成模型中，我們采用$\beta Normal(0,{\sigma }^2)$對季節性施加平滑先驗。

將序列截斷到 N，對季節性施加了低通濾波器，因此增加 N 可以適應更快變化的季節模式，盡管存在過度擬合的風險。對于年度和每周季節性，我們發現分別使用 N = 10 和 N = 3 對大多數問題效果良好。選擇這些參數可以使用諸如 AIC 的模型選擇過程進行自動化。

3.3、假日和活動事件

假期和事件對許多企業時間序列提供了大而有些可預測的沖擊，通常不遵循周期模式，因此它們的影響無法很好地通過平滑周期來建模。例如，美國的感恩節是在11月的第四個星期四舉行的。美國最大的電視節目之一——超級碗則在1月或2月的某個星期日舉行，難以編程聲明。世界上許多國家有根據農歷計算的重要節日。特定假期對時間序列的影響通常每年相似，因此將其納入預測非常重要。

我們允許分析師提供一個自定義的過去和未來事件列表，由該事件或假期的唯一名稱識別，如表1所示。我們包括一個國家列，以便除全球節日外，保留特定于國家的節日列表。對于給定的預測問題，我們使用全球節日集合和特定國家節日集合的并集。

將這個假期列表納入模型中是基于假設假期效應是獨立的。對于每個假期 i，設 $D_i$ 為該假期的過去和未來日期集合。我們添加一個指示函數，表示時間 t 是否在假期 i 期間，并為每個假期分配一個參數 ${\kappa }_i$，該參數是相應預測變化。這與季節性類似，通過生成回歸器矩陣來完成。

$Z(t)=[1(t\in D_1),...,1(t\in D_L)]$

并采用

$h(t)=Z(t)\kappa$ (7)

與季節性一樣，我們使用先驗$\kappa ～Normal(0,v^2)$。

通常，包括特定假期前后一段時間窗口的效應非常重要，比如感恩節周末。為了解決這個問題，我們為假期周圍的日期添加額外的參數，本質上將假期周圍的每一天都視為一個假期。

3.4、模型擬合

當將每個觀測的季節性和假期特征結合到矩陣X中，并將變化點指示符a(t)結合到矩陣A中時，模型(1)可以在幾行Stan代碼（Carpenter et al. 2017）中表示，如下所示。對于模型擬合，我們使用Stan的L-BFGS算法找到最大后驗估計，但也可以進行完整的后驗推斷，將模型參數的不確定性包括在預測的不確定性中。

圖4顯示了Prophet模型對圖3中Facebook事件時間序列的預測。這些預測與圖3中相同的三個日期一樣，僅使用該日期之前的數據進行預測。Prophet模型能夠預測每周和每年的季節性，與圖3中的基準模型不同，它不會對第一年的假期下降作出過度反應。在第一個預測中，Prophet模型在只有一年數據的情況下稍微過擬合了每年的季節性。在第三個預測中，模型還沒有學習到趨勢已經發生變化。圖5顯示了一個包含最近三個月數據的預測展示了趨勢的變化（虛線）。

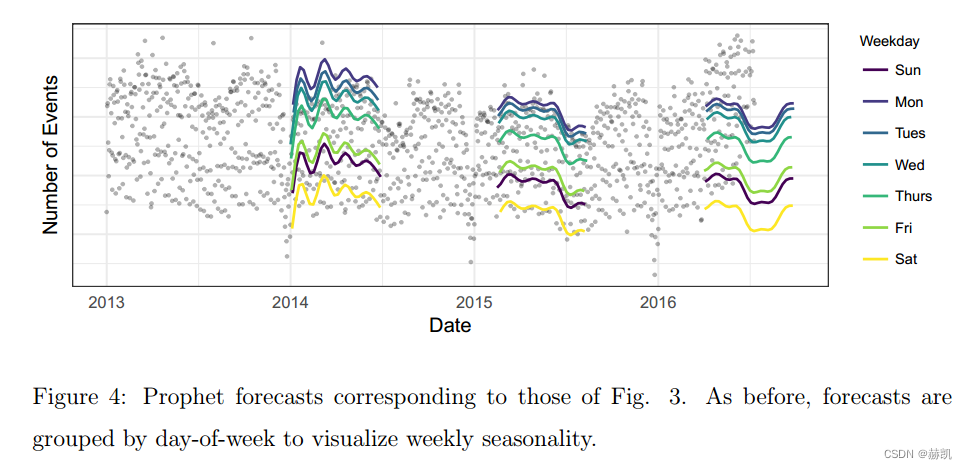
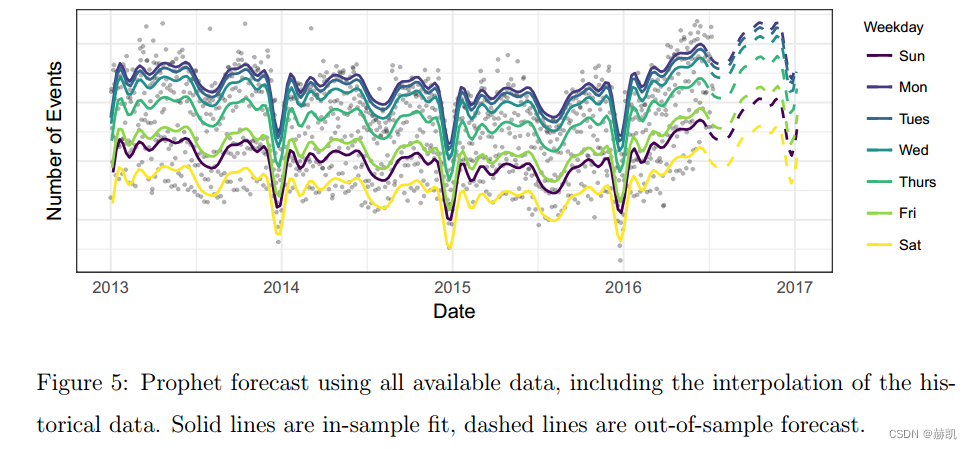
可分解模型的一個重要優勢是它允許我們分別觀察預測的每個組成部分。圖6顯示了與圖4中最后一個預測相對應的趨勢、每周季節性和每年季節性組件。除了產生預測之外，這為分析師提供了洞察他們的預測問題的有用工具。

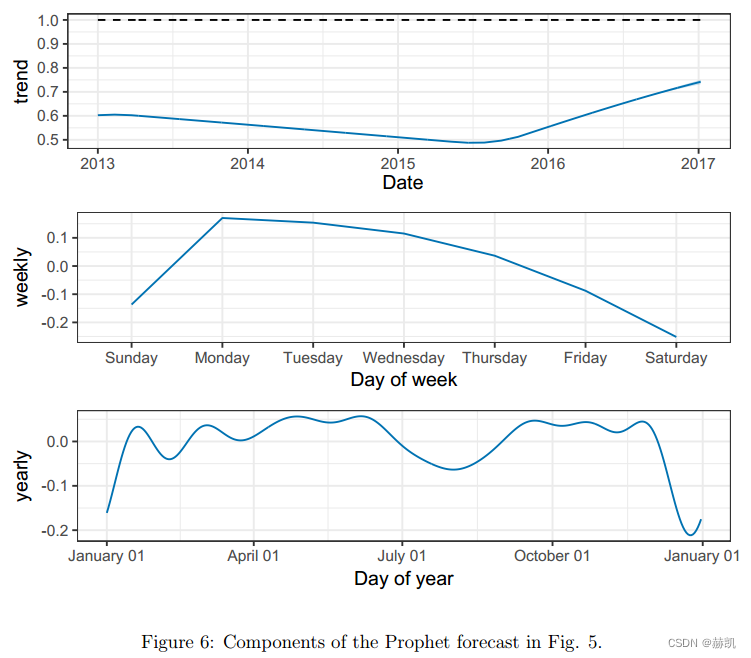
清單1中的參數tau和sigma是對模型變化點和季節性正則化程度的控制參數。正則化對于避免過擬合是重要的，然而，很可能沒有足夠的歷史數據通過交叉驗證來選擇最佳的正則化參數。我們設置了適用于大多數預測問題的默認值，并且當需要優化這些參數時，會與分析師進行協商。

3.5、分析師參與的循環建模

經常進行預測的分析師通常對其所預測的數量具有豐富的領域知識，但在統計知識方面卻知之甚少。在Prophet模型規范中，有幾個地方可以讓分析師調整模型以應用他們的專業知識和外部知識，而無需理解底層統計學。

• 能力：分析師可能擁有關于總市場規模的外部數據，并可以直接通過指定容量來應用這些知識。

• 變化點：已知的變化點日期，如產品變更日期，可以直接指定。

• 假期和季節性：我們合作的分析師具有哪些假期影響哪些地區增長的經驗，他們可以直接輸入相關的假期日期和適用的季節性時間尺度。

• 平滑參數：通過調整$\tau$，分析師可以從更全局或局部平滑的模型范圍內進行選擇。季節性和假期平滑參數$(\sigma ,\nu )$允許分析師告訴模型未來預期的歷史季節變化有多少。

借助良好的可視化工具，分析師可以使用這些參數來改進模型擬合。當將模型擬合繪制在歷史數據上時，很快就能發現自動變化點選擇中遺漏了哪些變化點。τ參數是一個單一的旋鈕，可以調整趨勢的靈活性，σ是調整季節性分量強度的旋鈕。可視化提供了許多其他有益的人為干預機會：線性趨勢或邏輯增長、確定季節性的時間尺度以及確定應該從擬合中剔除的異常時間段等。所有這些干預都可以在沒有統計專業知識的情況下進行，是分析師應用其見解或領域知識的重要途徑。

預測文獻通常區分基于歷史數據擬合的統計預測和人為判斷的預測（也稱為管理預測），后者由人類專家使用已經學到對特定時間序列有效的任何過程產生。這兩種方法各有其優勢。統計預測需要較少的領域知識和人類預測者的努力，并且可以輕松擴展到許多預測。人為判斷的預測可以包含更多信息，并且對變化的條件更具響應性，但可能需要分析師進行大量工作。

我們的分析師參與的循環建模方法是一種替代方法，試圖通過使分析師的努力集中于在必要時改進模型而不是通過某種未經說明的程序直接產生預測，從而融合了統計和人為判斷預測的優勢。我們發現我們的方法與Wickham和Grolemund（2016）提出的“轉換-可視化-建模”循環非常相似，其中人類領域知識在一些迭代之后被編碼到改進的模型中。

典型的預測擴展依賴于完全自動化的程序，但已經在許多應用中顯示，人為判斷的預測在準確性上表現出色。我們提出的方法讓分析師可以通過一小組直觀的模型參數和選項對預測進行判斷，同時保留在必要時回歸到完全自動化的統計預測的能力。截至目前，我們只有零星的實證證據表明可能會改進準確性，但我們期待未來的研究可以評估分析師在模型輔助設置中的改進效果。

在規模化的情況下，讓分析師參與其中的能力至關重要，這在很大程度上依賴于預測質量的自動評估和良好的可視化工具。我們現在描述如何自動化預測評估，以確定最相關的預測以供分析師輸入。

4、自動化預測評估

在本節中，我們概述了一種通過比較各種方法并確定需要手動干預的預測的流程來自動化預測績效評估的方法。這個部分與所使用的預測方法無關，并包含我們在多種應用中進行生產業務預測時制定的一些最佳實踐。

4.1、使用基線預測

在評估任何預測過程時，比較一組基線方法非常重要。我們喜歡使用簡單的預測方法，對底層過程進行強烈的假設，但在實踐中可以產生合理的預測。我們發現比較簡單的模型（最后一個值和樣本均值）以及第2節中描述的自動預測程序非常有用。

4.2、建模預測準確性

預測是在一定的時間范圍內進行的，我們用H表示這個范圍。這個范圍是我們關心預測未來多少天的數量，通常是30、90、180或365天。因此，對于任何具有每日觀察的預測，我們會產生高達H個未來狀態的估計，每個狀態都會與一些誤差相關聯。我們需要聲明一個預測目標來比較方法和跟蹤績效。此外，了解我們的預測過程有多容易出錯可以讓企業預測的使用者決定是否信任它。

設$\hat{y}(t|T)$表示用直到時間t的歷史信息對時間T進行的預測，并且$d(y,y^{\prime })$是距離度量，例如平均絕對誤差，$d(y,y^{\prime })=|y?y^{\prime }|$。距離函數的選擇應該是特定于問題的。De Gooijer和Hyndman（2006）回顧了幾種這樣的誤差度量{在實踐中，我們更喜歡平均絕對百分比誤差（MAPE）的可解釋性。我們將時間T之前$h\in (0,H]$時段的預測的經驗準確性定義為：

$?(T,h)=d(\hat{y}(T+h|T),y(T+h))$

為了對準確性及其隨h的變化進行估計，通常會指定誤差項的參數模型，并從數據中估計其參數。例如，如果我們使用AR(1)模型$y(t)=\alpha +\beta y(t?1)+\nu (t)$，我們會假設$\nu (t)～Normal(0,{\sigma }_v^2)$，并專注于從數據中估計方差項${\sigma }_v^2$。然后，我們可以通過模擬或使用錯誤總和的期望的解析表達式來使用任何距離函數形成期望。不幸的是，這些方法只在已經針對過程指定了正確模型的條件下給出正確的誤差估計，而這在實踐中不太可能發生。

我們更傾向于采用適用于各種模型的非參數方法來估計預期誤差。這種方法類似于在獨立同分布數據上對進行預測的模型估計外樣本誤差的交叉驗證。給定一組歷史預測，我們擬合一個關于不同預測時域h的預期誤差模型。

$\xi (h)=E[?(T,h)]$ (8)

該模型應該是靈活的，但也可以提出一些簡單的假設。首先，函數在h上應該是局部平滑的，因為我們預計連續幾天犯的錯誤相對類似。其次，我們可能會假設該函數在h上應該是微弱遞增的，盡管這并不適用于所有預測模型。在實踐中，我們使用局部回歸（Cleveland和Devlin 1988）或同位素回歸（Dykstra 1981）作為誤差曲線的靈活非參數模型。

為了生成歷史預測誤差以擬合該模型，我們使用一種稱為模擬歷史預測的過程。

4.3、模擬歷史預測

我們希望通過擬合（8）式中的預期誤差模型來進行模型選擇和評估。遺憾的是，使用類似交叉驗證的方法比較困難，因為觀測數據不可互換 - 我們不能簡單地隨機劃分數據。我們使用模擬歷史預測（SHFs）在歷史的不同截斷點處產生K個預測，這些截斷點被選擇為使預測時間段位于歷史之內，并且可以評估總體誤差。這個過程基于傳統的“滾動起源”預測評估程序（Tashman，2000），但只使用了一小組截斷日期，而不是每個歷史日期都進行一次預測。使用較少的模擬日期的主要優點是節約計算資源，同時提供更少相關性的準確度測量。

SHFs模擬了我們在過去的那些時間點上使用該預測方法所犯的誤差。圖3和圖4中的預測就是SHFs的例子。這種方法的優點是簡單易懂，容易向分析師和決策者解釋，而且用于生成對預測誤差的洞察相對無爭議。在使用SHF方法評估和比較預測方法時，需要注意兩個主要問題。

首先，我們進行的模擬預測越多，它們對誤差的估計就越相關。在極端情況下，如果在歷史的每一天進行一次模擬預測，考慮到額外的一天信息，預測不太可能發生太大變化，并且從一天到下一天的誤差幾乎相同。另一方面，如果我們只進行很少的模擬預測，那么我們就只有很少的歷史預測誤差觀測值可供我們基于其選擇模型。作為一種經驗法則，對于預測時間段為H，我們通常每隔H=2個周期進行一次模擬預測。盡管相關的估計不會引入模型準確度的偏差，但它們會產生較少有用的信息并減慢預測評估的速度。

其次，更多的數據可能導致預測方法的表現更好或更差。當模型規范錯誤且過度擬合過去時，更長的歷史可能會導致更糟糕的預測，例如使用樣本均值來預測具有趨勢的時間序列。圖7顯示了LOESS方法在圖3和圖4的時間序列上使用的預測期間的預期平均絕對百分比誤差函數ξ(h)的估計值。該估計是使用九個模擬預測日期進行的，每個季度開始后選擇一個日期。Prophet在所有預測時間段上都具有較低的預測誤差。Prophet的預測是使用默認設置進行的，調整參數可能進一步提高性能。

在可視化預測時，我們更喜歡使用點而不是線來表示歷史數據，因為這些點代表精確的測量結果，永遠不會進行插值。然后，我們通過預測疊加線條。對于SHFs，將模型在不同預測時間段上的誤差可視化是有用的，既可以作為時間序列（如圖3），也可以作為SHFs的匯總（如圖7）。

即使對于單個時間序列，SHFs也需要計算許多預測，而且在規模上，我們可能希望對許多不同的指標以及多個不同的聚合級別進行預測。只要這些機器可以寫入相同的數據存儲，SHFs可以在獨立的機器上進行計算。我們將預測和相關誤差存儲在Hive或MySQL中，具體取決于它們的預期使用方式。

4.4、識別大的預測誤差

當有太多的預測需要分析師手動檢查時，能夠自動識別可能存在問題的預測就變得非常重要。自動識別不良預測可以讓分析師更有效地利用有限的時間，并利用他們的專業知識來糾正任何問題。以下是使用SHFs來識別預測可能存在問題的幾種方法：

• 當相對于基準線而言，預測誤差較大時，可能是因為模型規范錯誤。分析師可以根據需要調整趨勢模型或季節性模型。

• 對于特定日期，所有方法都存在較大的誤差，這可能是異常值的表現。分析師可以識別并排除異常值。

• 當某個方法的SHF誤差從一個截斷點急劇增加到下一個截斷點時，這可能表明數據生成過程發生了變化。添加變點或將不同階段分開建模可能會解決這個問題。

雖然有些問題無法輕易糾正，但我們遇到的大多數問題都可以通過指定變點和排除異常值來糾正。一旦預測被標記為需要審核并可視化，這些問題就很容易被識別和糾正。

5、結論

規模化預測的一個重要主題是，具有不同背景的分析師必須進行比他們能夠手動完成的更多的預測。我們預測系統的第一個組成部分是我們在Facebook上對各種數據進行多次迭代預測后開發的新模型。我們使用簡單、模塊化的回歸模型，通常使用默認參數效果良好，并允許分析師選擇與他們的預測問題相關的組件，并根據需要輕松進行調整。第二個組成部分是用于測量和跟蹤預測準確性，并標記應該手動檢查的預測的系統，以幫助分析師進行增量改進。這是一個關鍵的組成部分，它可以讓分析師識別何時需要對模型進行調整，或者何時可能需要完全不同的模型。簡單、可調整的模型和可擴展的性能監控結合起來，使大量分析師能夠對大量和多樣的時間序列進行預測，這就是我們所認為的規模化預測。

6、致謝

我們感謝Dan Merl讓Prophet的開發成為可能，并在開發過程中提供建議和見解。我們還感謝Dirk Eddelbuettel、Daniel Kaplan、Rob Hyndman、Alex Gilgur和Lada Adamic對本文的有益審閱。我們特別感謝Rob Hyndman將我們的工作與主觀預測聯系起來的見解。

至此結束，主要是作者能把公式列出來就比較厲害。