空間映射(SM)是一種公認的加速電磁優化的方法。現有的SM方法大多基于順序計算機制。本文提出了一種用于電磁優化的并行SM方法。在該方法中，每次迭代開發的代理模型被訓練以同時匹配多個點的精細模型。多點訓練和SM使代理模型在比標準SM更大的鄰域內有效。本文提出的多點代理模型訓練方法本質上適合于并行計算，并通過并行計算實現。這包括并行的多個精細模型評估和使用并行算法的多點代理訓練。與標準模型相比，該方法進一步減少了模型的迭代次數，加快了優化過程。通過三個微波濾波器實例說明了該技術。

SM優化公式
標準SM 1：是指在每次迭代[1]中使用單點精細模型數據訓練代理模型的公式
標準SM 2：是指每次迭代中的代理模型都用當前和之前所有迭代積累的精細模型數據進行訓練的公式
并行SM優化算法
所提出的優化將被制定為一個框架與一個粗模型的框架，開發代理模型使用并行處理，并使用代理模型進行設計優化。粗模型選擇與現有的SM方法相同。下面提出了一種使用并行計算方法的替代建模。

在多點上的代理建模

在該方法中，為了建立一個快速、準確的代理模型，以準確地**表示較大鄰域內的精細模型，我們開發了代理模型來在多個點上匹配精細模型。對于每個多個點**，都應該進行一次良好的模型評估。在這些點上的精細模型響應數據，用于訓練代理模型。這類點的數量隨著設計變量的數量的增加而增加。我們選擇了一種抽樣方法來減少點的數量。最常見的兩種樣本分布是網格分布和星形分布。

在實驗中 candes等人對信號在傅里葉空間的變換系數進行極坐標星形抽樣，獲得了非常好的還原效果

當設計變量數目n較小時，網格分布抽樣方法是可行的。然而，當n變大時，網格分布導致數據點呈指數增長。此外，如此大的數據量也使得訓練的計算成本更高。因此，星形分布是首選[23]，因為隨著n的增加，點的數量呈線性增長。

在我們提出的SM公式中，每次迭代都使用星形分布。在第6次迭代中，我們在代理模型Xk的最優解周圍生成了多個星形分布的樣本點。圖1顯示了我們提出的多點采樣方法來訓練代理模型。在本文中，我們將Xk作為第6次迭代中星形分布的中心點。我們沿每個維度擾動中心點兩次，一次向正方向，一次向負方向。根據粗模型靈敏度確定各設計參數的偏差百分比。按照星形分布策略，我們在中心周圍找到精細模型的其他2n個點。
設Xk(1)，Xk(2)，…Xk(2n+1)，表示以Xk(1)為中心的起始分布的2n+1個點，即Xk(1)=Xk，其余2n個點位于該中心的鄰域。當優化過程移動到下一次迭代時，星形分布的中心從Xk移動到Xk+1。所有其他的星形分布中的點也相應移動，如圖所示
如圖1所示。

使用并行方法計算

精細的模型數據生成通常只占總計算時間的主要計算負擔，如果我們使用順序計算方法，數據樣本的數據生成需要乘以精細模型評估的計算時間

提出了一種使用多個處理器并行生成精細模型數據的方法。利用并行處理器在這些星形分布點上進行了精細的模型評估。并行加速因子和并行效率作為我們的優化方法的性能標準的一部分。開銷成本與每次迭代中的數據樣本的生成相關聯，例如，并行運行的多個處理器之間的通信時間。設加速為單個處理器上的數據生成時間與并行處理器上的數據生成時間之間的比率

在我們提出的方法中，精細模型數據生成使用并行計算方法來生成EM數據。同樣，在優化代理模型以匹配2n+1個點的精細模型數據的訓練過程中，也使用并行計算來減少建模時間，從而在優化過程中實現進一步的加速。在訓練過程中，必須對所有數據采樣點迭代求代理模型與數據之間的訓練誤差，以及該誤差相對于映射參數的導數。這個計算是代理訓練計算的主要部分。因此，我們將多點訓練數據分成2n+1個獨立的訓練數據集，由2n+1個處理器并行使用。并行計算2n+1個訓練誤差及其導數，然后合并得到總訓練誤差和總訓練誤差的導數。訓練過程的并行加速和并行效率的定義與精細模型數據的并行生成相似。

并行SM優化算法

在本節中，我們將描述我們所提出的并行SM優化的總體算法。
首先，用單元映射初始化映射函數，

使用單元映射，初始代理模型等于粗模型。然后利用粗模型進行設計優化，通過求解找到粗模型x*?的初始最優解

其中，表示與粗輸入變量向量對應的粗模型的響應向量

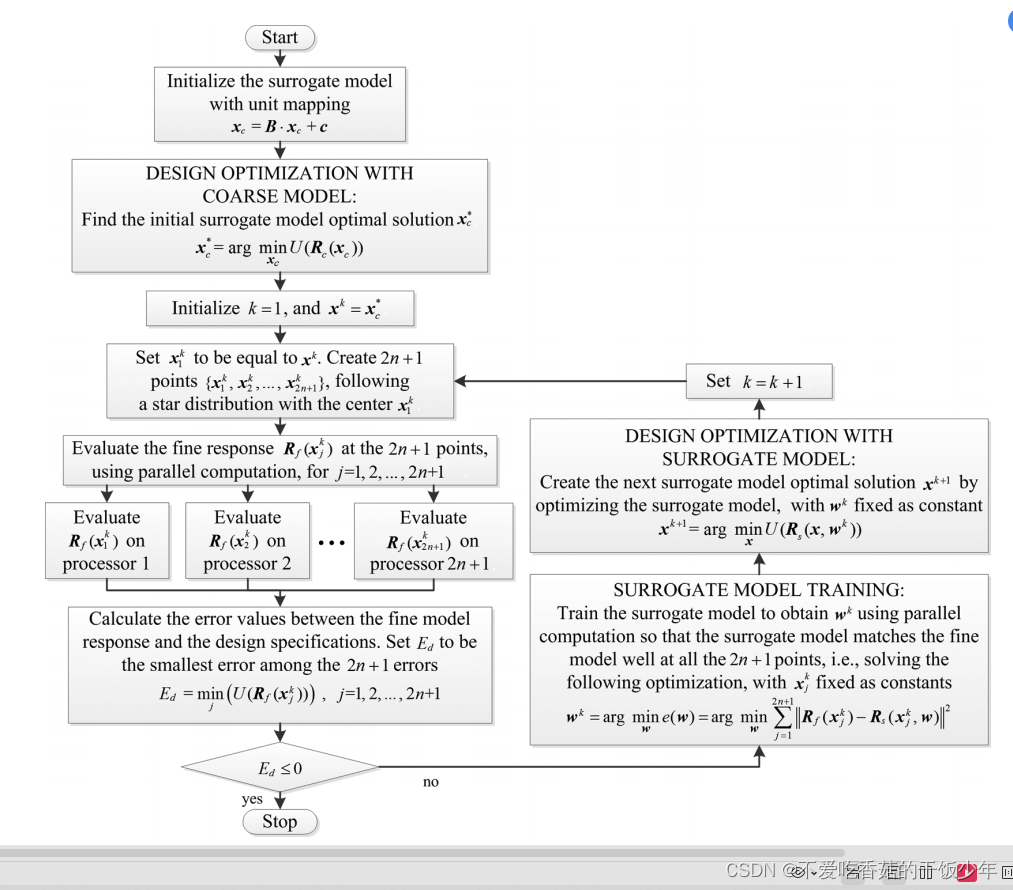
用單元映射初始化代理模型→粗模型設計優化:尋找初始代理模型的最優解