2023年IEEE IOTJ SCI1區TOP，動態環境下無人機目標覆蓋任務路徑規劃，深度解析+性能實測

1.摘要

無人機（UAV）作為物聯網應用的重要工具，正廣泛應用于智能農業監測、智能交通監測等領域，并逐漸成為國內外研究熱點。然而，現有飛行路徑規劃算法在可行性與有效性方面仍存在不足。本文針對動態環境下無人機目標覆蓋任務路徑規劃問題，提出了一種基于貪心分配與改進蟻群優化算法（ACO-VP），該算法首先通過貪心策略確定最優無人機數量并合理分配目標點；隨后在蟻群算法中引入可變信息素增強因子和揮發系數，優化信息素更新機制以提升規劃效率；并在目標點動態增加時實現路徑的實時重規劃。仿真結果表明，該方法在覆蓋效率與路徑優化效果方面均優于傳統算法。

2.問題模型

環境描述

參數定義

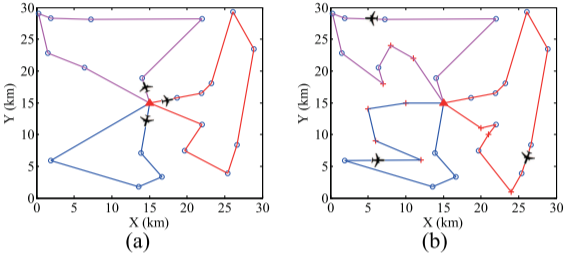
本文設定的應用場景為森林火災監測，區域內若干目標點被標記為易發火位置，為實現實時
監測與異常檢查，多架無人機被調度執行覆蓋任務。目標點集合記為 $P=\mathcal{P}=$
${P1,P2,…,PN}\{P_1,P_2,\ldots,P_N\}$ ,無人機集合記為 $U={U1,U2,…,UM}\mathcal{U}=\{U_1,U_2,\ldots,U_M\}$ 。無人機需從基站出發并
返回，覆蓋區域內所有目標點，且每個點僅能被一架無人機訪問一次。

在任務執行過程中，若出現新的目標點，則需將其納入覆蓋范圍，路徑規劃需實時更新。此時，無人機需從當前位置重新規劃航跡，覆蓋剩余目標點并最終返回基站。

成本函數

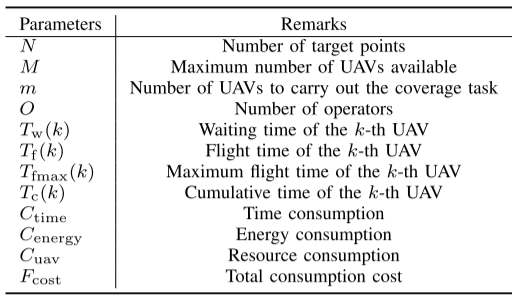
為優化多無人機覆蓋任務的飛行軌跡，本文構建了綜合成本函數。將無人機起飛前的準備時間定義為等待時間 $T_w(k)$ ,其與操作員數量相關，并隨無人機順序累積。飛行時間 $T_f(k)$ 表示無人機完成所有目標點訪問及返回基站所需時間，由飛行距離與轉角時間共同決定。累計時間 $T_c(k)$ 定義為等待時間與飛行時間之和。

約束條件包括：無人機飛行時間不得超過電池續航限制；每個目標點必須且只能由一架無人機訪問；路徑需保證連通性；無人機數量不得超過上限。

綜合成本函數：
$Fcost=w1Ctime+w2Cenergy+w3CuavF_\mathrm{cost}=w_1C_\mathrm{time}+w_2C_\mathrm{energy}+w_3C_\mathrm{uav}$

3.算法設計

算法分為兩個階段：任務分配和路徑規劃。在第一階段，采用貪心分配策略確定任務所需的無人機數量，并將目標點分配給各無人機；在第二階段，提出基于可變信息素蟻群優化算法（ACO-VP），為選定的無人機規劃最優路徑。

貪心分配策略

在每一步迭代中，將飛行時間最短的目標點分配給當前累計時間最小的無人機，并更新其路徑與狀態，直至所有目標點分配完畢。

首先計算完成任務所需的最小無人機數 $MminM_\mathrm{min}$ ,并得到其對應的基準成本值。隨后，對從 $MminM_\mathrm{min}$ 到最大無人機數 $M$ 的不同情況逐一采用貪心策略，生成任務分配方案，并計算相應的綜合成本函數 $Fcost(m)F_{\mathrm{cost}}(m)$ 。通過比較不同 $m$ 的結果，最終確定最優無人機數量及其最優任務分配方案。

可變信息素蟻群優化算法（ACO-VP）

為提高搜索效率和收斂速度，本文提出了一種基于可變信息素改進蟻群算法（ACO-VP），該方法通過在信息素更新規則中引入可變信息素增強因子和可變信息素揮發系數。

在信息素增量模型中，引入可變信息素增強因子 $ν\nu$ ,用于增強第 $t$ 次迭代中的信息素濃度。當本次迭代的最優解優于上一迭代的最優解時，在對應路徑上增加額外信息素，以加快正反饋討程中的信息素沉積：
$ν(t)={QL?(t),if?L?(t)<L0,otherwise\nu(t) = \begin{cases} \dfrac{Q}{L^*(t)}, & \text{if } L^*(t) < L \\ 0, & \text{otherwise} \end{cases}$

信息素更新：
$τij(t+1)=(1?ρ)τij(t)+ρ[Δτij(t)+ν(t)]\tau_{ij}(t+1)=(1-\rho)\tau_{ij}(t)+\rho[\Delta\tau_{ij}(t)+\nu(t)]$

信息素揮發系數 $ρ\rho$ 對算法收斂速率影響顯著。當 $ρ\rho$ 過小，殘余信息素難以揮發，收斂速度顯著降低；當 $ρ\rho$ 過大，收斂雖加快，但易陷入局部最優。因此，引入可變揮發系數 $ρ\rho$ ：
$ρ(t+1)={1?0.9(1?ρ(t)),if?δ<0.001ρ(t),otherwise\rho(t+1) = \begin{cases} 1 - 0.9\bigl(1 - \rho(t)\bigr), & \text{if } \delta < 0.001 \\ \rho(t), & \text{otherwise} \end{cases}$

4.結果展示

論文仿真

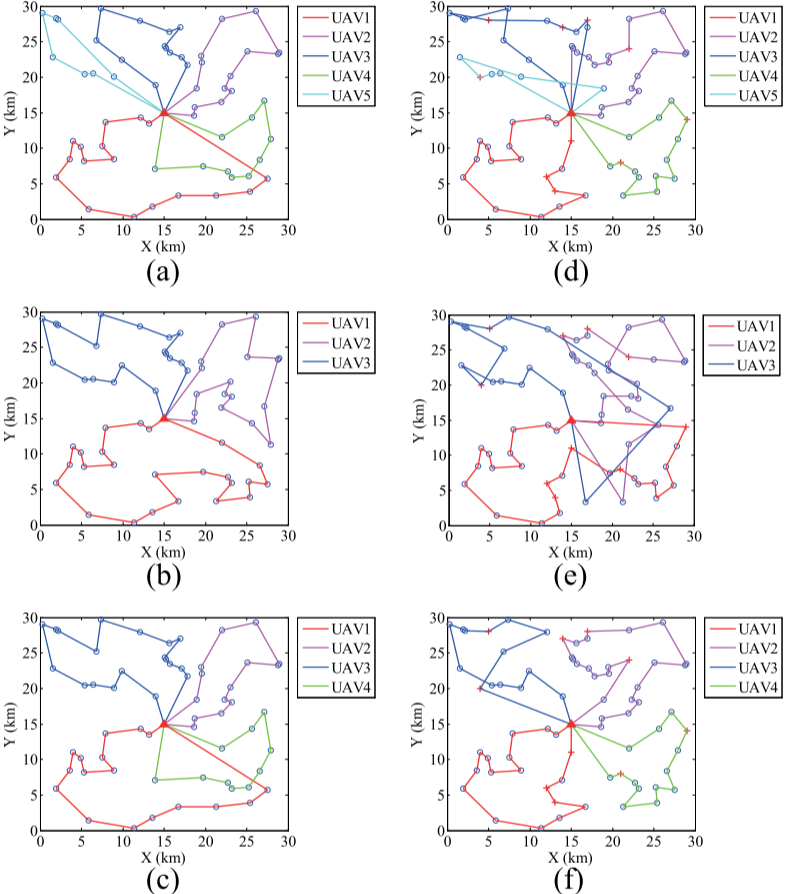
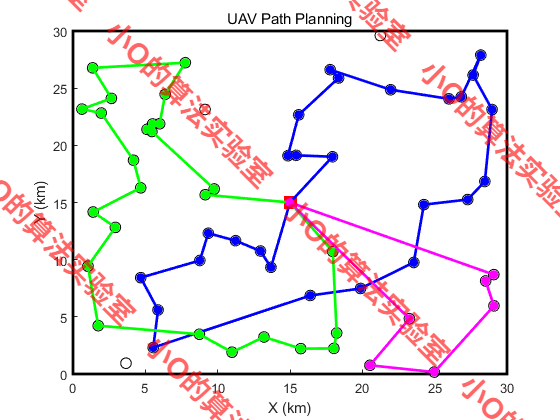
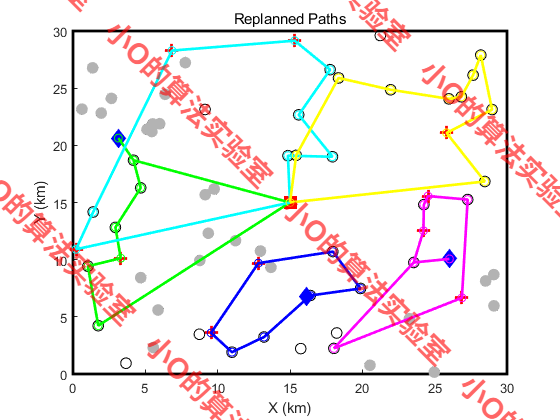
5.參考文獻

[1] Li J, Xiong Y, She J. UAV path planning for target coverage task in dynamic environment[J]. IEEE Internet of Things Journal, 2023, 10(20): 17734-17745.

6.代碼獲取

7.算法輔導·應用定制·讀者交流

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/diannao/97529.shtml
繁體地址，請注明出處：http://hk.pswp.cn/diannao/97529.shtml
英文地址，請注明出處：http://en.pswp.cn/diannao/97529.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！