在Numpy庫中有專門的linalg 模塊用來做線性代數相關的運算。
本文中線性代數的一般概念不會解釋
拆解矩陣
鳶尾花數據矩陣結構如下(150 × 4):
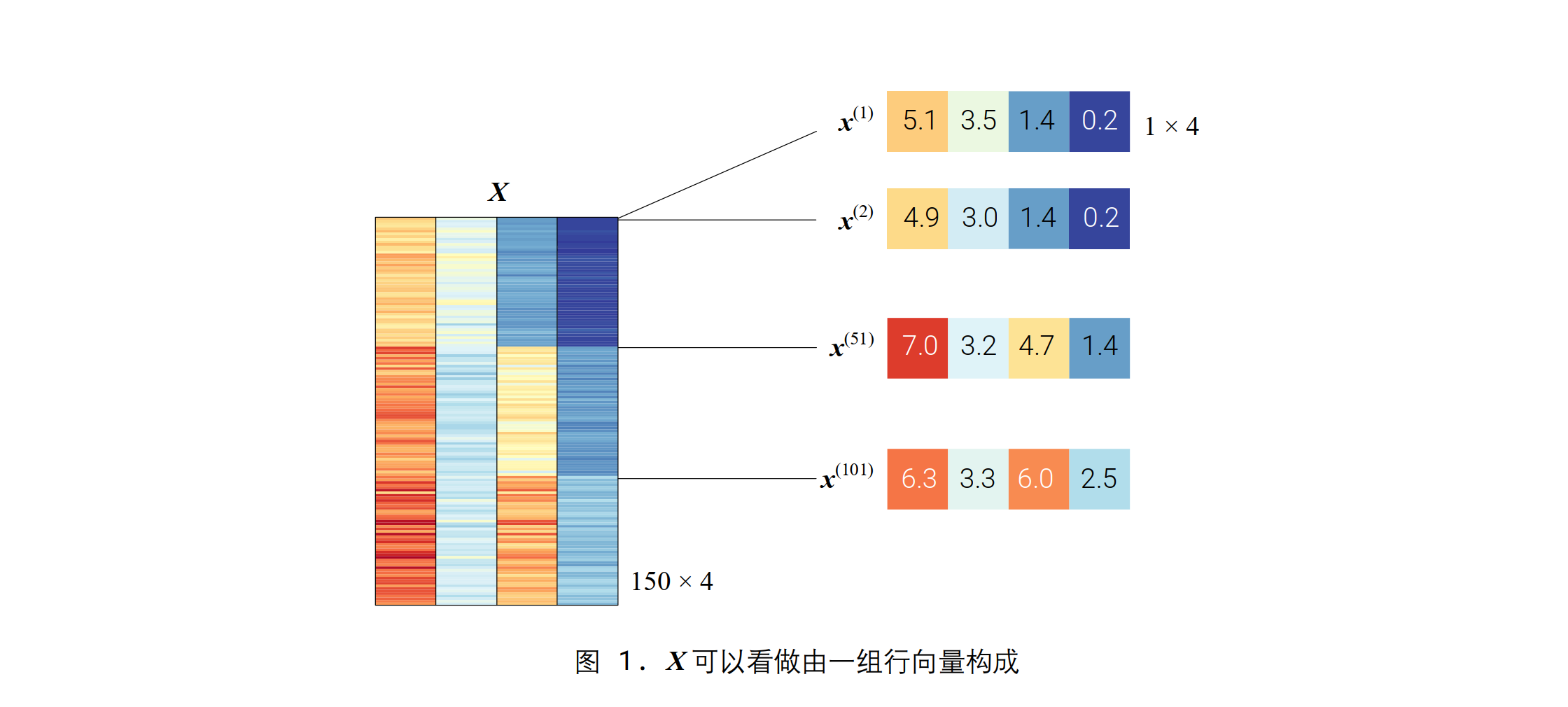
取其中的行向量和列向量:
# 導入包
import numpy as np
from sklearn.datasets import load_iris
# 從sklearn導入鳶尾花數據
iris = load_iris()
X = iris.data
# 提取四個行向量 (二維數組)
x_row_1 = X[[1 - 1], :]
x_row_2 = X[[2 - 1], :]
x_row_51 = X[[51 - 1], :]
x_row_101 = X[[101 - 1], :]# 提取四個列向量 (二維數組)
x_col_1 = X[:, [0]]
x_col_2 = X[:, [1]]
x_col_3 = X[:, [2]]
x_col_4 = X[:, [3]]
向量運算
向量的模
norm_x_row_1 = np.linalg.norm(x_row_1)
norm_x_row_2 = np.linalg.norm(x_row_2)
norm_x_row_51 = np.linalg.norm(x_row_51)
norm_x_row_101 = np.linalg.norm(x_row_101)
向量單位化
unit_x_row_1 = x_row_1 / norm_x_row_1
unit_x_row_2 = x_row_2 / norm_x_row_2
unit_x_row_51 = x_row_51 / norm_x_row_51
unit_x_row_101 = x_row_101 / norm_x_row_101
向量內積
inner_prod_x_row_1_2 = np.dot(x_row_1[0], x_row_2[0])
inner_prod_x_row_1_51 = np.dot(x_row_1[0], x_row_51[0])
inner_prod_x_row_1_101 = np.dot(x_row_1[0], x_row_101[0])
向量夾角
下面的代碼先求內積是因為單位向量的內積就是余弦值
# 計算單位向量內積
dot_product_1_51 = np.dot(unit_x_row_1[0],unit_x_row_51[0])
# 將結果轉化為弧度
angle_1_51 = np.arccos(dot_product_1_51)
# 將結果轉化為角度
angle_1_51 = np.rad2deg(angle_1_51)
這里補充一個數學上的概念:

矩陣運算
矩陣乘法
# 第一個格拉姆矩陣
G = X.T @ X
# 第二個格拉姆矩陣
H = X @ X.T
矩陣的逆
# 計算格拉姆矩陣G的逆矩陣
a G_inv = np.linalg.inv(G)
幾個常見矩陣分解
Cholesky 分解
# 對格拉姆矩陣G進行Cholesky分解
a L = np.linalg.cholesky(G)
G是正定陣
特征值分解 EVD
# 對格拉姆矩陣G進行特征值分解
Lambdas, V = np.linalg.eig(G)
Lambdas的對角線是特征值,V的每一列是特征向量
奇異值分解 SVD
# 鳶尾花數據矩陣X奇異值分解
U,S,VT = np.linalg.svd(X, full_matrices = False)






的深度語義理解繪制新航線)
)


 RDB和AOF有什么區別?)



)


![Linux應用軟件編程---網絡編程(TCP并發服務器構建:[ 多進程、多線程、select ])](http://pic.xiahunao.cn/Linux應用軟件編程---網絡編程(TCP并發服務器構建:[ 多進程、多線程、select ]))

)