545C 貪心 1500
題意:給 n 棵樹在一維數軸上的坐標 xix_ixi? ,以及它們的長度 hih_ihi?。現在要你砍倒這些樹,樹可以向左倒也可以向右倒,砍倒的樹不能重合、當然也不能覆蓋其他的樹原來的位置,現在求最大可以砍倒的樹的數目。
一眼以為是dp,但是感覺處理左右轉移很麻煩,瞟了眼題解…是很易懂的貪心…
分析:
- 兩邊的樹向兩邊倒,不妨礙中間的樹
- 中間的樹只考慮左右相鄰的距離,直觀考慮一邊倒的情況較好,互不干擾
- 統一向左倒
- 不能向左,向右有兩種情況
- 右邊的樹可以向左倒,倒就完了,我全都要
- 右邊的樹不能倒,或可以向右倒,本次的樹是否向右倒不影響這倆樹的貢獻,倒就完了
struct tr
{int x,h;
};
void solve(){int n;cin>>n;vector<tr>t(n+1);forr(i,1,n){cin>>t[i].x>>t[i].h;}if(n==1)return cout<<1<<endl,void();//t[1]和t[n]向兩邊倒 一定有貢獻int ans=0;forr(i,2,n-1){if(t[i].x-t[i].h>t[i-1].x){ans++;//向左倒// cout<<i<<'l'<<endl;}else if(t[i].x+t[i].h<t[i+1].x){//向右倒t[i].x+=t[i].h;ans++;// cout<<i<<'r'<<endl;}}cout<<ans+2<<endl;
}
550C 思維 枚舉 1500

100位數,只能用string存
先考慮啥樣的數能被8整除
8 16 24 32 40 48… 1000…
發現千位的數一定能被8整除,只考慮低三位數能不能被整除,取s中的數枚舉組合,計算量1e6,能過。
void solve(){string s;cin>>s;int l=s.size();string ans;forr(i,0,l-1){int a=(s[i]-'0');forr(j,i+1,l-1){int b=(s[j]-'0');forr(k,j+1,l-1){int c=(s[k]-'0');int tp=a*100+b*10+c;if(tp%8==0)return cout<<"YES"<<endl<<tp<<endl,void();}int tpp=(a*10+b);if(tpp%8==0)return cout<<"YES"<<endl<<tpp<<endl,void();}if(a%8==0)return cout<<"YES"<<endl<<a<<endl,void();}cout<<"NO"<<endl;
}
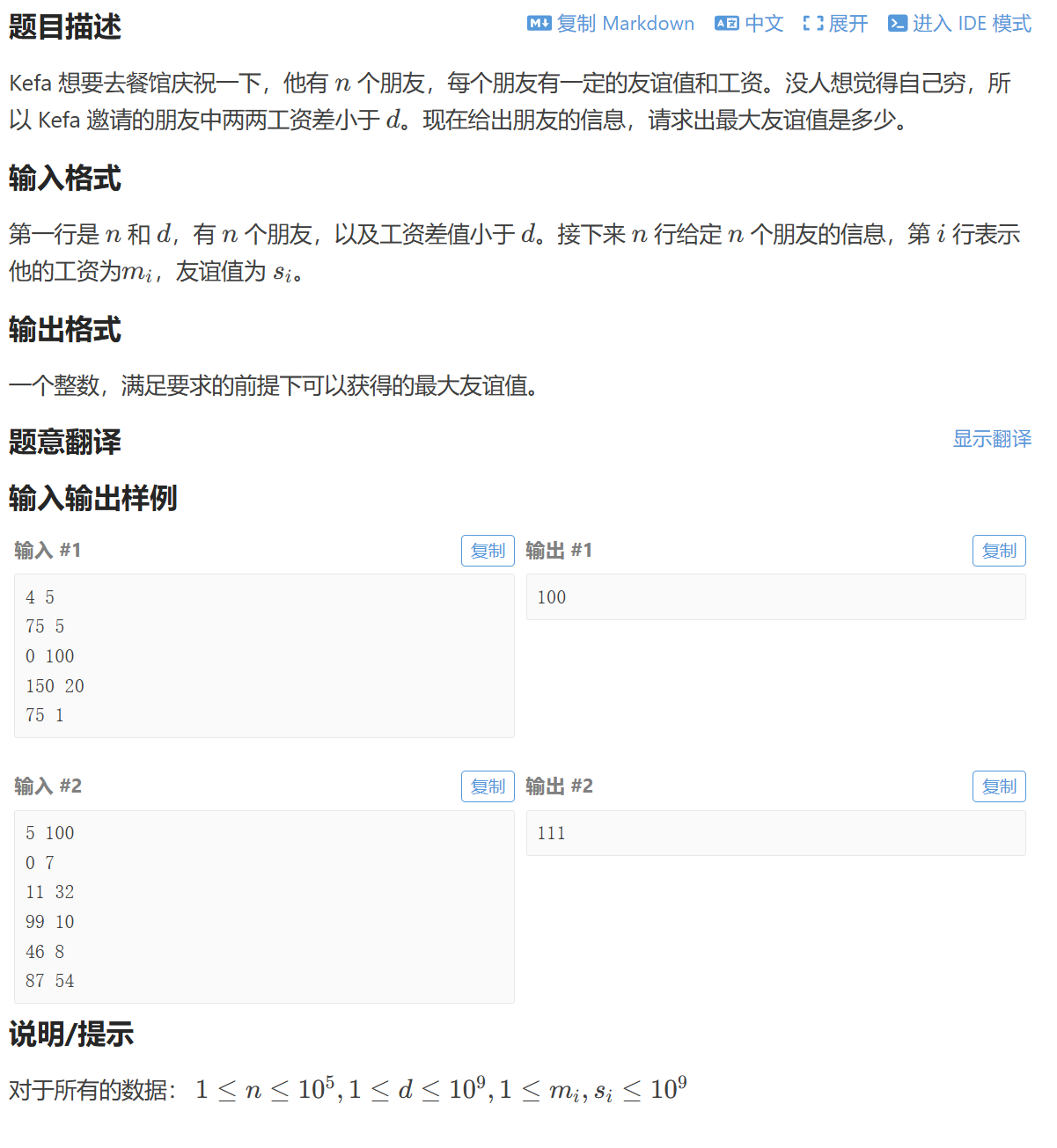
580B 雙指針 1500
簡單尺取法水題
struct fri
{int m,s;
};void solve(){int n,d;cin>>n>>d;vector<fri>f(n+1);forr(i,1,n){cin>>f[i].m>>f[i].s;}sort(f.begin()+1,f.end(),[](fri x,fri y){return x.m<y.m;});int sum=0;int l=1,r=1,ans=0;while (r<=n){if(f[r].m-f[l].m<d){sum+=f[r].s;ans=max(sum,ans);// cout<<ans<<endl;r++;}else sum-=f[l].s,l++;}cout<<ans<<endl;
}
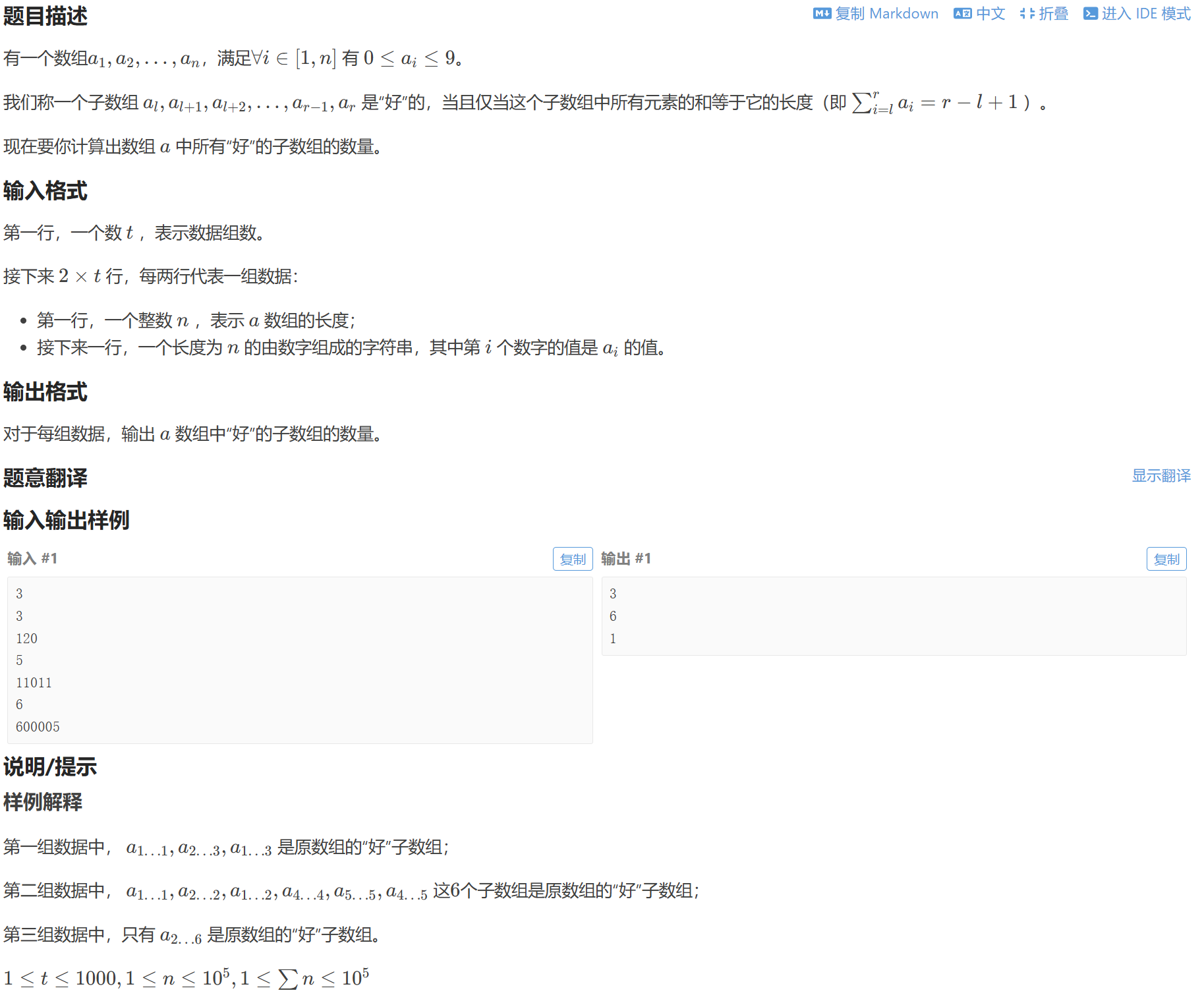
1398C 前綴和 找規律 1600
分析:
- 連續元素的和 考慮前綴和
- ∑i=lrai=sumr?suml?1=r?(l?1)sumr?r=suml?1?(l?1)\sum^r_{i=l}a_i=sum_r-sum_{l-1}=r-(l-1) \\ sum_r-r=sum_{l-1}-(l-1)∑i=lr?ai?=sumr??suml?1?=r?(l?1)sumr??r=suml?1??(l?1)
所以求出所有tpi=sumi?itp_i=sum_i-itpi?=sumi??i,相等的兩個tpitp_itpi?可以組成一個好數組
void solve(){int n;cin>>n;string s;cin>>s;vector<int>a(n+1),sm(n+1,0),tp(n+1);forr(i,1,n){a[i]=s[i-1]-'0';}forr(i,1,n){sm[i]=a[i]+sm[i-1];tp[i]=sm[i]-i;}map<int,int>m;m[0]=1;int ans=0;forr(i,1,n)ans+=(m[tp[i]]++);//注意兩兩組合是怎樣計數的cout<<ans<<endl;
}
550A 思維 暴力 1500
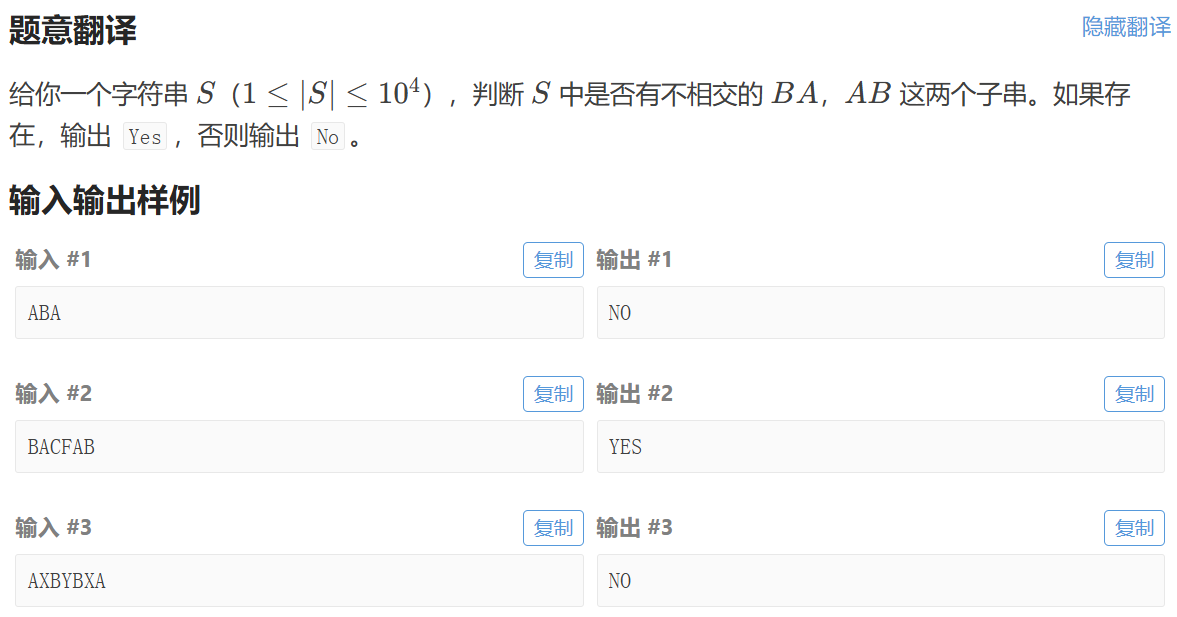
情況要想得全一點
ABA no
AXBXA no
ABBA yes
ABABA yes
BABAB yes
BABA no
分析:
- 先找到AB,枚舉每一個AB在的地方,把AB替換成X,再找有沒有BA(但是這樣會超時
- BABAB發現找兩個AB的位置就可以
void solve()
{string s;cin>>s;int len=s.size();int ab=s.find("AB");if(ab!=-1)//暴力枚舉ab{string tp=s;tp.replace(ab,2,"X");int ba=tp.find("BA");if(ba!=-1)return cout<<"YES"<<endl,void();}ab=s.rfind("AB");if(ab!=-1)//暴力枚舉ab{string tp=s;tp.replace(ab,2,"X");int ba=tp.find("BA");if(ba!=-1)return cout<<"YES"<<endl,void();}cout<<"NO"<<endl;
}




)
)













