1. MAE與MSE的本質區別

MAE（Mean Absolute Error）和MSE（Mean Squared Error）是兩種常用的損失函數，它們的數學形式決定了對誤差的不同敏感程度：

• MAE： $\text{MAE}=\frac{1}{n}{\sum }_{i=1}^n|y_i?{\hat{y}}_i|$
• MSE： $\text{MSE}=\frac{1}{n}{\sum }_{i=1}^n(y_i?{\hat{y}}_i{)}^2$

從幾何角度看，MSE等價于歐氏距離的平方，而MAE等價于曼哈頓距離。這導致MSE對離群點更加敏感，而MAE更具魯棒性。

2. 高斯噪聲下的統計特性

在噪聲服從高斯分布 $?～\mathcal{N}(0,{\sigma }^2)$ 的假設下：

1. MSE是最優損失函數
   MSE對應于高斯噪聲下的最大似然估計（MLE）。此時，最小化MSE等價于最大化對數似然函數：
   $$\arg \underset{\theta }{\min }\sum _{i=1}^n(y_i?f(x_i;\theta ){)}^2?\arg \underset{\theta }{\max }\prod _{i=1}^n\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left(?\frac{(y_i?f(x_i;\theta ){)}^2}{2{\sigma }^2}\right)$$
   高斯分布的二次指數形式直接對應平方誤差。

2. MAE的統計假設
   MAE對應于噪聲服從拉普拉斯分布時的MLE。拉普拉斯分布的概率密度函數為：
   $$p(?)=\frac{1}{2b}\exp \left(?\frac{|?|}{b}\right)$$

   $$\arg \underset{\theta }{\min }\sum _{i=1}^n|y_i?f(x_i;\theta )|?\arg \underset{\theta }{\max }\prod _{i=1}^n\frac{1}{2b}\exp \left(?\frac{|y_i?f(x_i;\theta )|}{b}\right)$$
   此時，最小化MAE等價于最大化拉普拉斯分布下的對數似然。

3. MAE導致稀疏解的內在機制

MAE容易產生稀疏解的根本原因在于其梯度特性：

1. MAE的梯度恒定
   MAE的梯度為：
   $$\frac{?\text{MAE}}{?\theta }=?\begin{array}{ll}+1,& \text{if?}{y}_i?f(x_i;\theta )>0\\ ?1,& \text{if?}{y}_i?f(x_i;\theta )<0\\ \text{undefined},& \text{if?}{y}_i?f(x_i;\theta )=0\end{array}$$
   當參數接近零時，梯度仍保持恒定（±1），促使參數快速收斂到零。

2. MSE的梯度衰減
   MSE的梯度為：
   $$\frac{?\text{MSE}}{?\theta }=?2(y_i?f(x_i;\theta ))?\frac{?f(x_i;\theta )}{?\theta }$$
   當誤差接近零時，梯度趨近于零，導致參數更新變得非常緩慢，難以徹底消除小參數。

3. 幾何解釋
   從優化角度看，MAE的等高線是菱形（在二維空間中），其頂點位于坐標軸上；而MSE的等高線是圓形。當損失函數的最小值靠近坐標軸時，MAE的等高線更容易與坐標軸相交，從而使某些參數被置零。更多可見 損失函數的等高線與參數置零的關系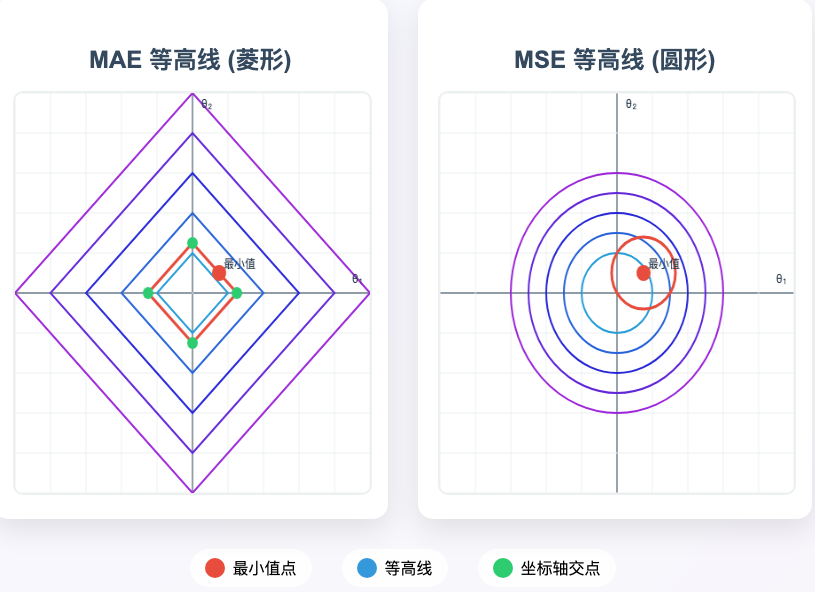

   

4. 對比總結

特性	MSE	MAE
對離群點敏感度	高（平方放大誤差）	低（線性處理誤差）
噪聲分布假設	高斯分布	拉普拉斯分布
梯度特性	梯度隨誤差減小而衰減	梯度恒定（除零點外）
稀疏性	不易產生稀疏解	易產生稀疏解
優化穩定性	平滑優化，數值穩定性好	非光滑優化，可能需要特殊處理

在實際應用中，如果數據包含較多離群點或需要進行特征選擇，MAE是更合適的選擇；如果追求預測精度且噪聲近似高斯分布，MSE通常表現更好。